Jak wykonać test levene’a w spss

Test Levene’a służy do określenia, czy dwie lub więcej grup ma równe wariancje.

Jest szeroko stosowany, ponieważ wiele testów statystycznych opiera się na założeniu, że grupy mają równe wariancje .

W tym samouczku wyjaśniono, jak wykonać test Levene’a w SPSS.

Przykład: test Levene’a w SPSS

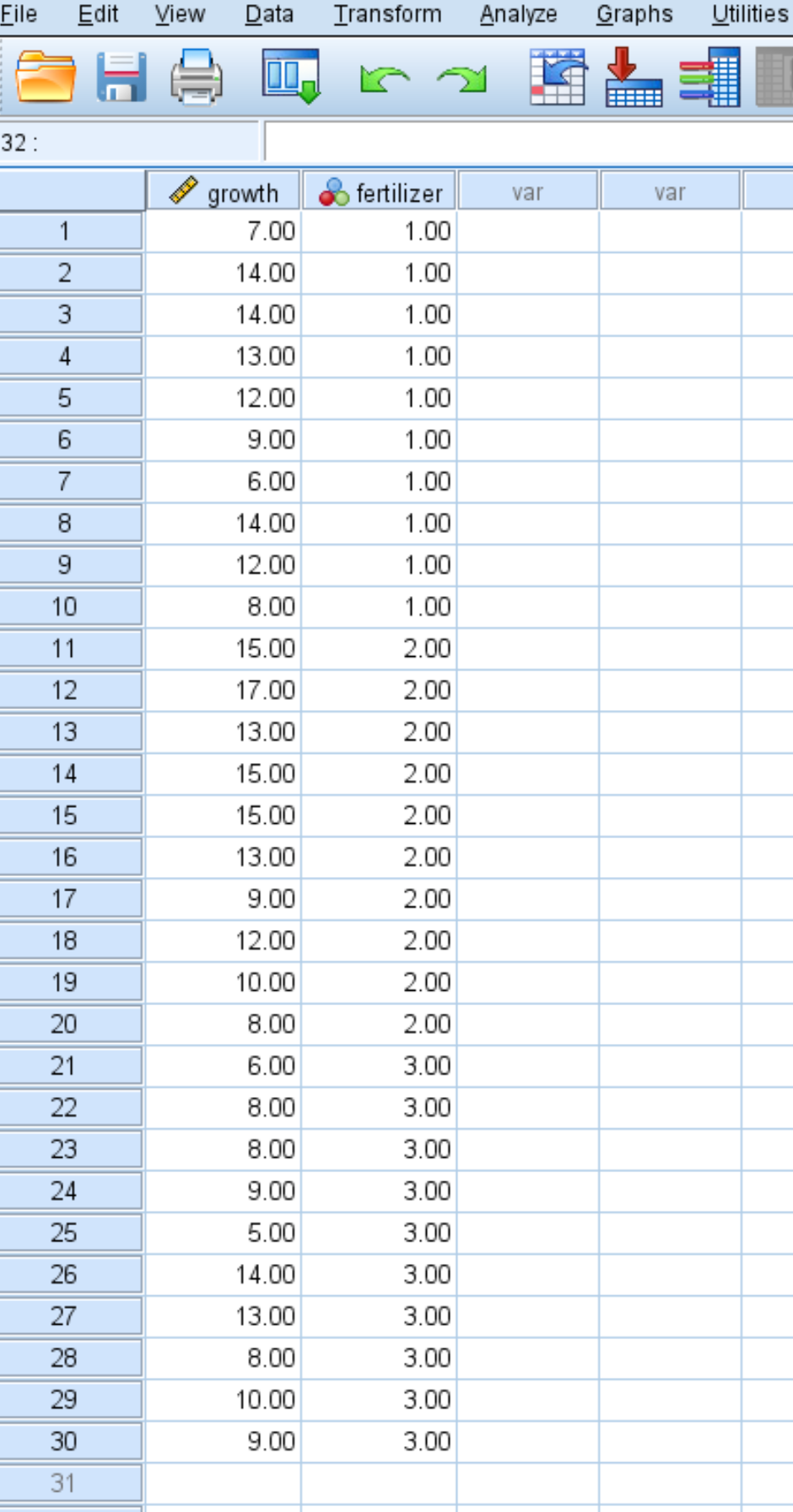
Naukowcy chcą wiedzieć, czy trzy różne nawozy prowadzą do różnych poziomów wzrostu roślin.

Losowo wybierają 30 różnych roślin i dzielą je na trzy grupy po 10, stosując do każdej grupy inny nawóz. Po miesiącu mierzą wysokość każdej rośliny.

Poniższy zrzut ekranu pokazuje wielkość wzrostu (w calach) każdej pojedynczej rośliny wraz z nawozem (1, 2 lub 3), który został zastosowany na roślinę:

Wykonaj poniższe kroki, aby wykonać test Levene’a w SPSS w celu ustalenia, czy trzy grupy mają równe wariancje.

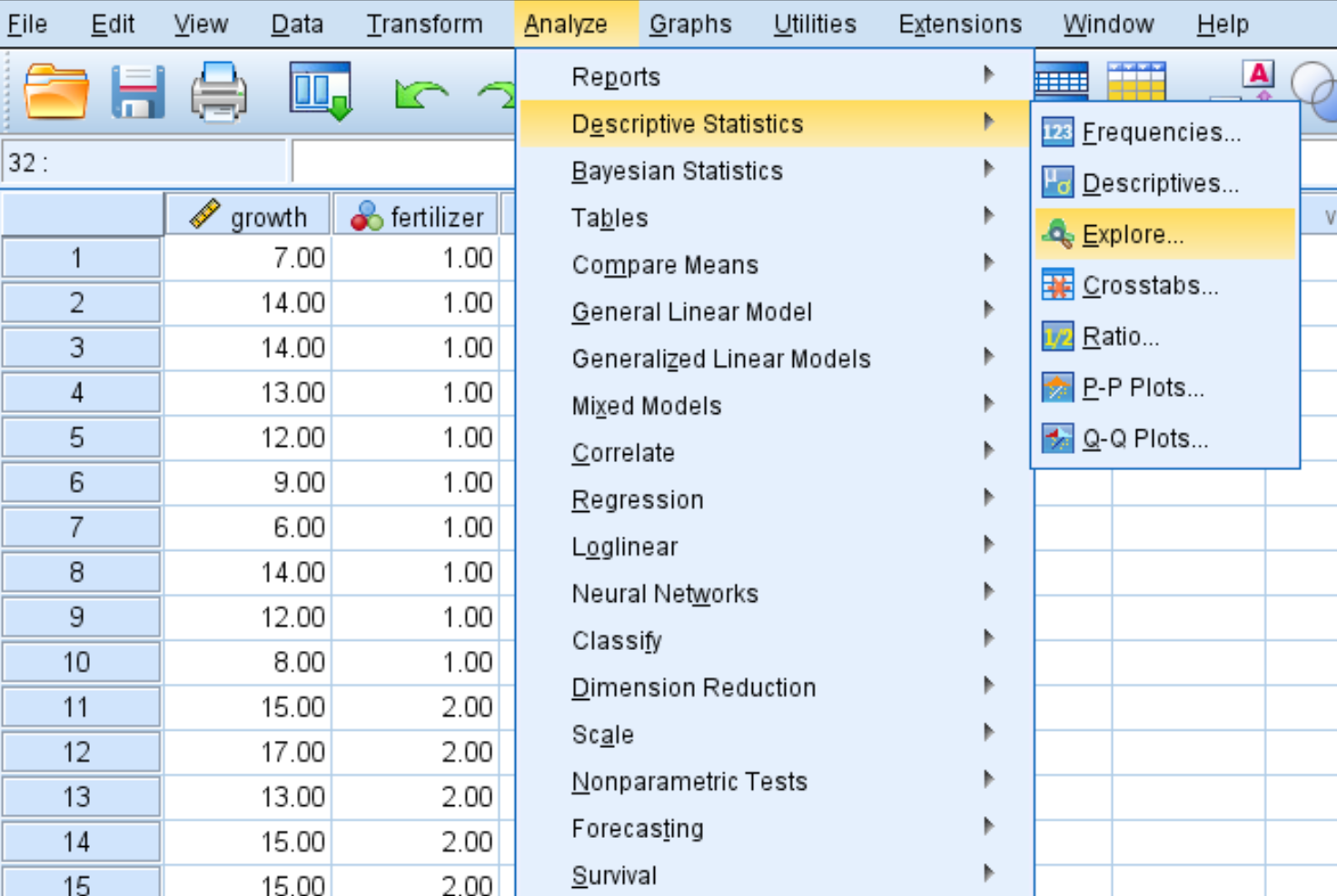
Krok 1: Wybierz opcję Eksploruj.

Kliknij kartę Analizuj , następnie Statystyki opisowe i Eksploruj :

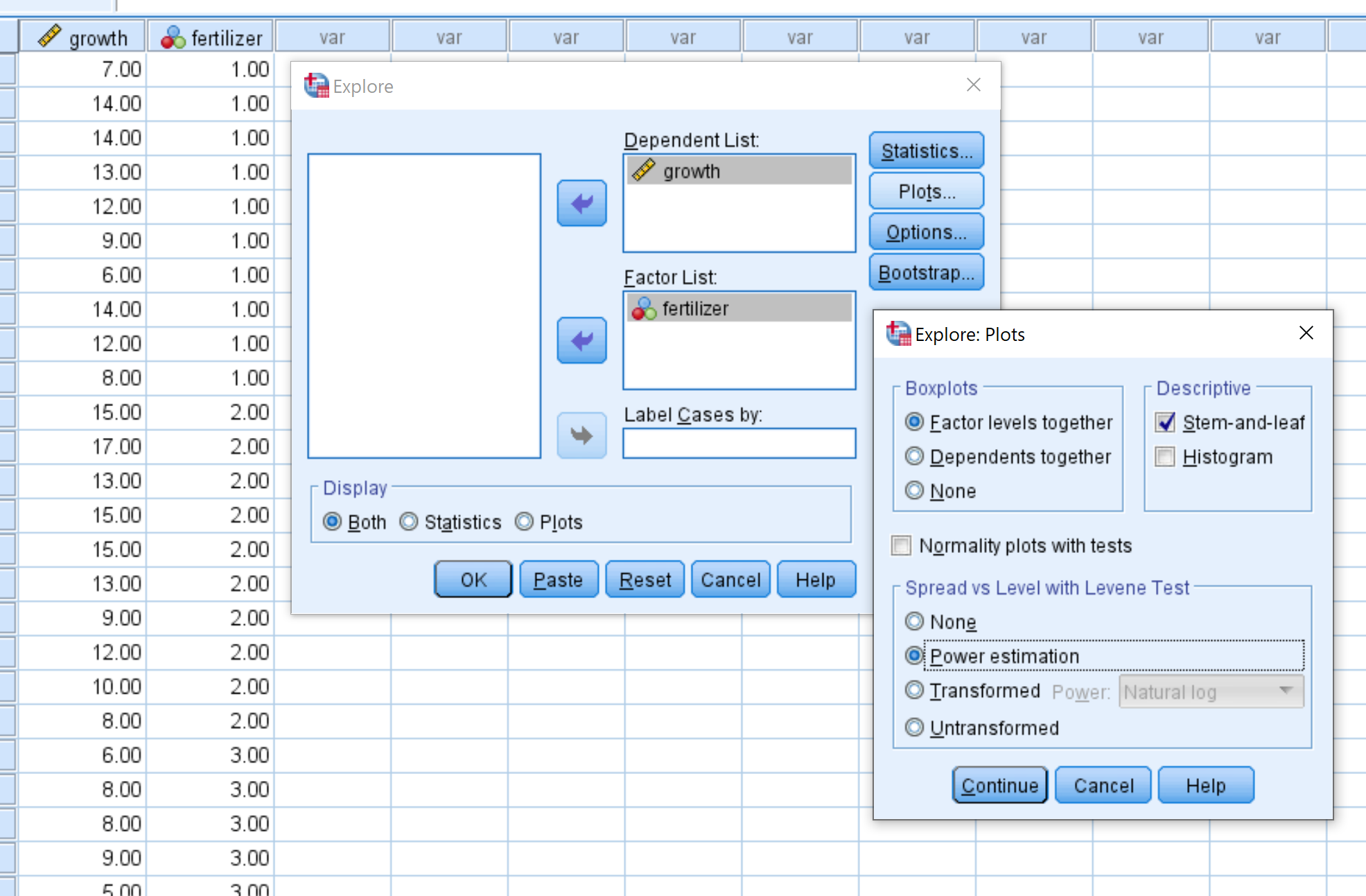
Krok 2: Wpisz niezbędne wartości, aby przeprowadzić test.

Przeciągnij wzrost do pola pod Listą Zależną i przeciągnij nawóz   w polu pod listą czynników.

Następnie kliknij Wykresy i upewnij się, że wybrano opcję Szacowanie mocy . Następnie kliknij Kontynuuj . Następnie kliknij OK .

Krok 3: Interpretacja wyników.

Po kliknięciu OK zostaną wyświetlone wyniki testu Levene’a:

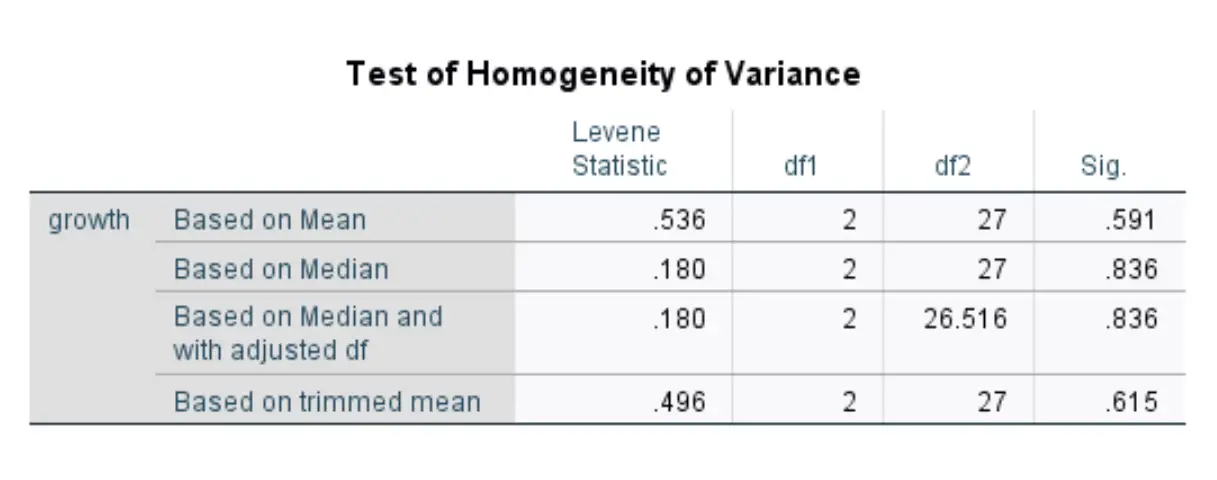
W poniższej tabeli przedstawiono statystyki testu dla czterech różnych wersji testu Levene’a. Interesujące nas liczby znajdują się w pierwszym wierszu, w którym wyświetlane są wyniki testu Levene’a na podstawie średniej.

Statystyka testowa wynosi 0,536 , a odpowiadająca jej wartość p wynosi 0,591* .

Ponieważ ta wartość p jest nie mniejsza niż 0,05, nie możemy odrzucić hipotezy zerowej.

Oznacza to, że nie mamy wystarczających dowodów, aby stwierdzić, że różnice we wzroście roślin pomiędzy trzema nawozami są znacząco różne.

Innymi słowy, trzy grupy mają równe wariancje. Gdybyśmy przeprowadzili test statystyczny (np. jednokierunkową ANOVA ), który zakłada, że każda grupa ma równą wariancję, wówczas założenie to zostałoby spełnione.

* Ta wartość p odpowiada statystyce F wynoszącej 0,536 z licznikiem df = 2 i mianownikiem df = 27. Tę wartość p można również obliczyć za pomocą kalkulatora rozkładu F.