Jak wykonać prostą regresję liniową w spss

Prosta regresja liniowa to metoda, której możemy użyć do zrozumienia związku między zmienną predykcyjną a zmienną odpowiedzi.

W tym samouczku wyjaśniono, jak przeprowadzić prostą regresję liniową w SPSS.

Przykład: Prosta regresja liniowa w SPSS

Załóżmy, że mamy następujący zbiór danych, który pokazuje liczbę przepracowanych godzin i oceny z egzaminów uzyskane przez 20 uczniów:

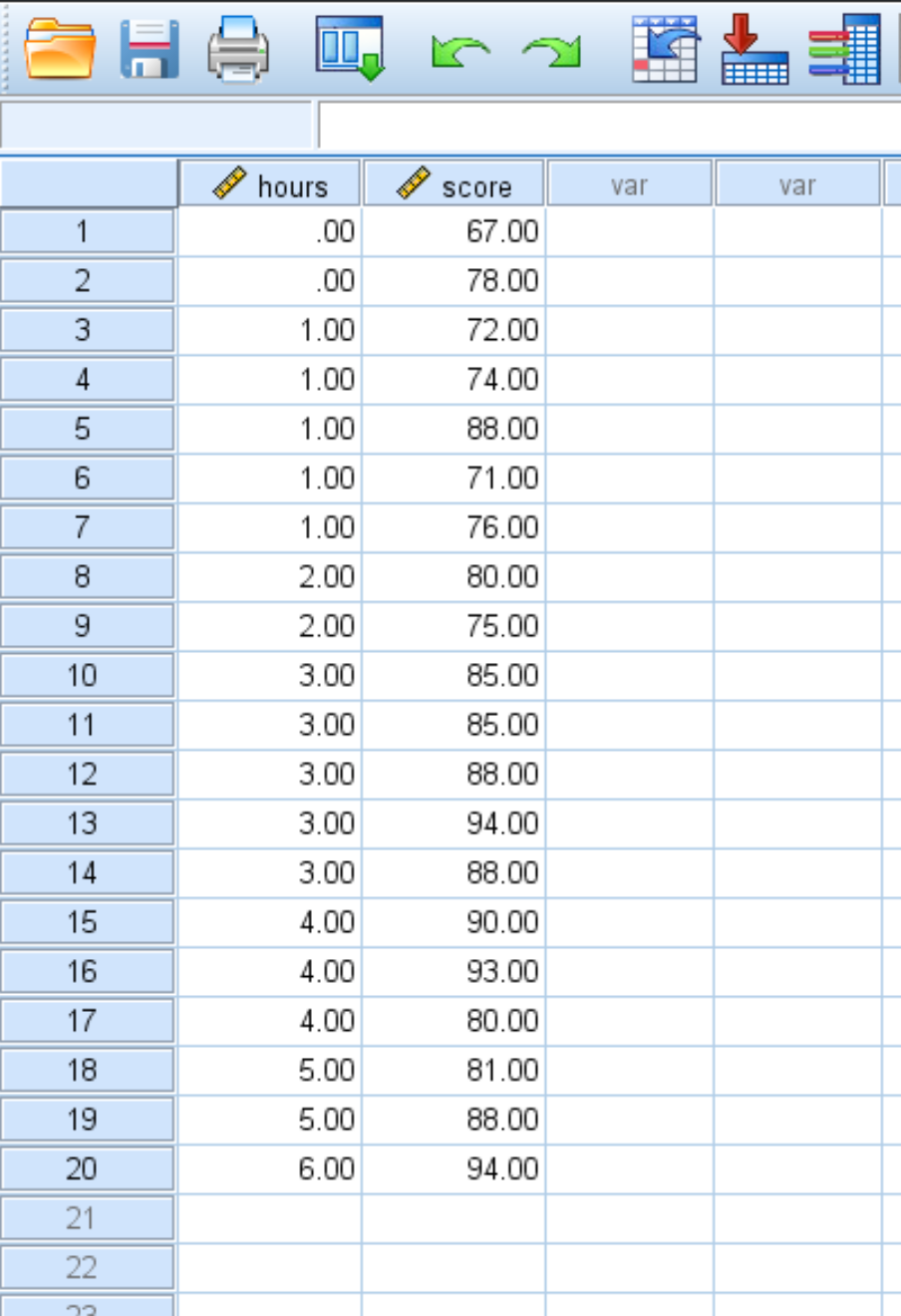
Wykonaj poniższe kroki, aby przeprowadzić prostą regresję liniową tego zbioru danych i określić ilościowo związek między przestudiowanymi godzinami a wynikiem egzaminu:

Krok 1: Wizualizuj dane.

Najpierw utworzymy wykres rozrzutu, aby zwizualizować związek między godzinami a wynikiem, aby upewnić się, że związek między dwiema zmiennymi wydaje się być liniowy. W przeciwnym razie prosta regresja liniowa nie będzie odpowiednią techniką.

Kliknij kartę Wykresy , a następnie kliknij opcję Kreator wykresów :

Z menu Wybierz z kliknij i przeciągnij Scatter/Dot do głównego okna edycji. Następnie przeciągnij zmienne czasy na oś x, a wynik na oś y.

Po kliknięciu OK pojawi się następujący wykres punktowy:

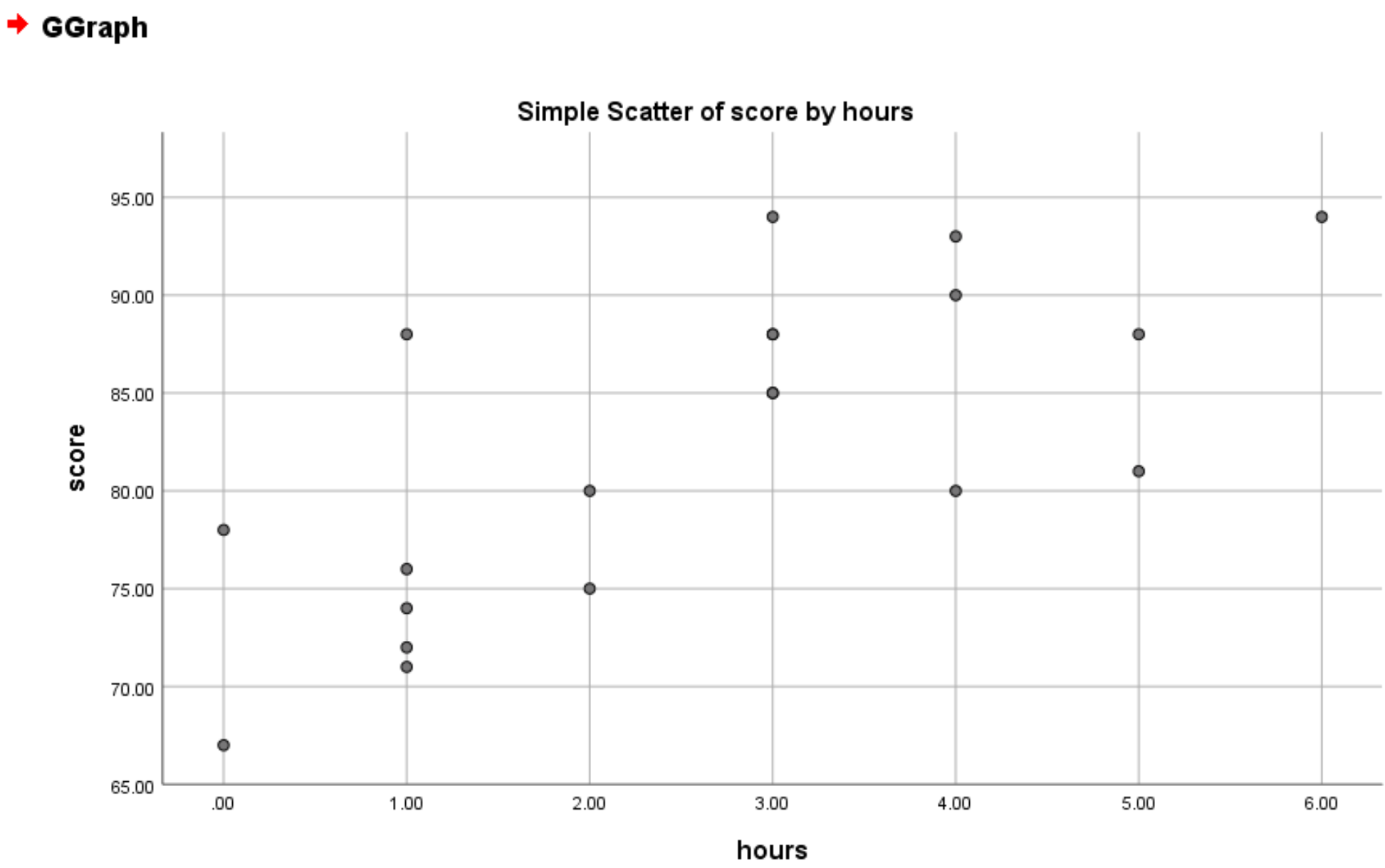
Z wykresu widać, że istnieje dodatnia liniowa zależność pomiędzy liczbą godzin a wynikiem. Ogólnie rzecz biorąc, studenci, którzy studiują więcej godzin, zwykle uzyskują wyższe wyniki.

Ponieważ istnieje wyraźna liniowa zależność między tymi dwiema zmiennymi, przystąpimy do dopasowania prostego modelu regresji liniowej do zbioru danych.

Krok 2: Dopasuj prosty model regresji liniowej.

Kliknij kartę Analiza , następnie Regresja , a następnie Liniowa :

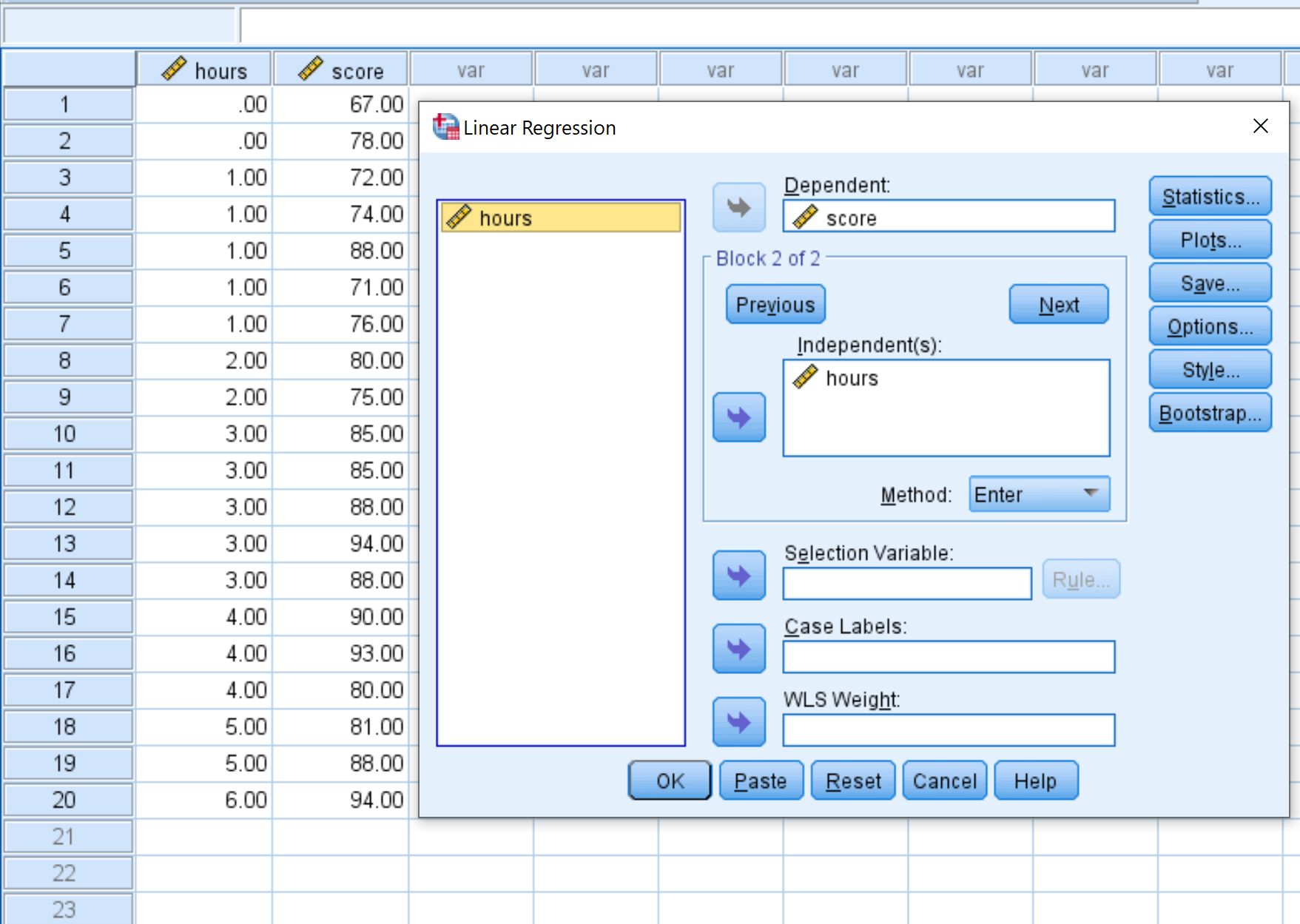
W nowym oknie, które się pojawi, przeciągnij wynik zmienny do pola Zależne i przeciągnij godziny do pola Niezależne. Następnie kliknij OK .

Krok 3: Interpretacja wyników.

Po kliknięciu OK pojawią się wyniki prostej regresji liniowej. Pierwszą tabelą, która nas interesuje, jest ta zatytułowana Podsumowanie modelu :

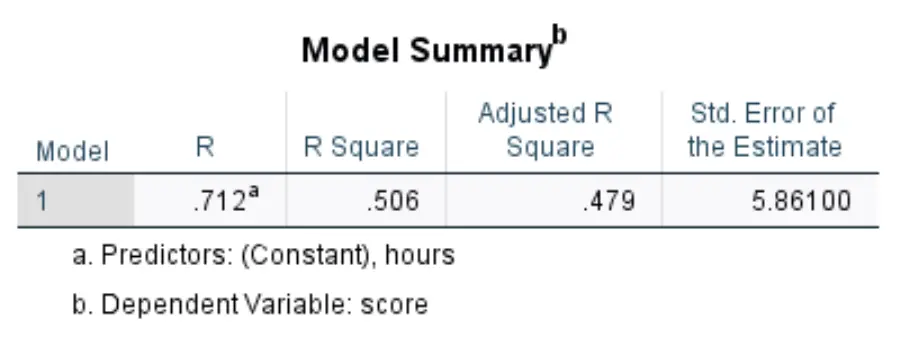
Oto jak interpretować najbardziej odpowiednie liczby w tej tabeli:

• Kwadrat R: Jest to proporcja wariancji zmiennej odpowiedzi, którą można wyjaśnić za pomocą zmiennej objaśniającej. W tym przykładzie 50,6% różnic w wynikach egzaminów można wyjaśnić liczbą przepracowanych godzin.
• Standard. Błąd estymacji: błąd standardowy to średnia odległość pomiędzy obserwowanymi wartościami a linią regresji. W tym przykładzie zaobserwowane wartości odbiegają średnio o 5861 jednostek od linii regresji.

Poniższa tabela, która nas interesuje, nosi tytuł Współczynniki :

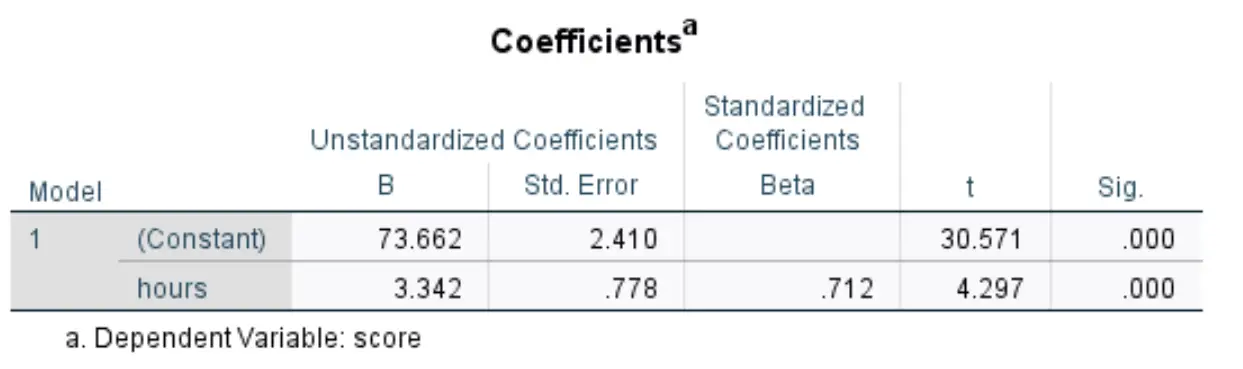
Oto jak interpretować najbardziej odpowiednie liczby w tej tabeli:

• Niestandaryzowane B (stała) : mówi nam o średniej wartościzmiennej odpowiedzi , gdy zmienna predykcyjna wynosi zero. W tym przykładzie średni wynik egzaminu wynosi 73,662 , gdy liczba godzin nauki wynosi zero.
• B niestandaryzowany (godziny): mówi nam o średniej zmianie zmiennej odpowiedzi powiązanej ze wzrostem o jedną jednostkę zmiennej predykcyjnej. W tym przykładzie każda dodatkowa godzina nauki wiąże się ze wzrostem wyniku egzaminu średnio o 3342 punkty.
• Sig (godziny): Jest to wartość p powiązana ze statystyką testową w godzinach. W tym przypadku, ponieważ wartość ta jest mniejsza niż 0,05, możemy stwierdzić, że zmienna predykcyjna godziny jest istotna statystycznie.

Na koniec możemy utworzyć równanie regresji, korzystając z wartości stałej i godzin . W tym przypadku równanie wyglądałoby następująco:

Szacowany wynik egzaminu = 73,662 + 3,342*(godziny)

Możemy użyć tego równania, aby znaleźć szacowany wynik egzaminu ucznia na podstawie liczby przestudiowanych godzin.

Przykładowo student studiujący 3 godziny powinien uzyskać na egzaminie wynik 83,688:

Szacowany wynik egzaminu = 73,662 + 3,342*(3) = 83,688

Krok 4: Ogłoś wyniki.

Na koniec chcemy podsumować wyniki naszej prostej regresji liniowej. Oto przykład, jak to zrobić:

Przeprowadzono prostą regresję liniową, aby określić ilościowo związek między przestudiowanymi godzinami a oceną z egzaminu. Do analizy wykorzystano próbę 20 uczniów.

Wyniki wykazały, że istnieje statystycznie istotna zależność pomiędzy przepracowanymi godzinami a oceną z egzaminu (t = 4,297, p < 0,000), a przepracowane godziny odpowiadały za 50,6% wyjaśnionej zmienności ocen z egzaminu. egzamin.

Równanie regresji okazało się następujące:

Szacowany wynik egzaminu = 73,662 + 3,342*(godziny)

Każda dodatkowa godzina nauki wiąże się ze wzrostem wyniku egzaminu średnio o 3342 punkty .

Dodatkowe zasoby

Poniższe samouczki wyjaśniają, jak wykonywać inne typowe zadania w SPSS:

Jak wykonać wielokrotną regresję liniową w SPSS
Jak wykonać regresję kwadratową w SPSS
Jak przeprowadzić regresję logistyczną w SPSS