Jak wykonać regresję kwadratową w spss

Kiedy dwie zmienne są ze sobą powiązane liniowo, często można zastosować prostą regresję liniową do ilościowego określenia ich związku.

Jednak prosta regresja liniowa nie działa dobrze, gdy dwie zmienne mają związek nieliniowy. W takich przypadkach można spróbować zastosować regresję kwadratową .

W tym samouczku wyjaśniono, jak przeprowadzić regresję kwadratową w SPSS.

Przykład: regresja kwadratowa w SPSS

Załóżmy, że chcemy zrozumieć związek pomiędzy liczbą przepracowanych godzin a szczęściem. Mamy następujące dane dotyczące liczby godzin przepracowanych tygodniowo i raportowanego poziomu szczęścia (w skali od 0 do 100) dla 16 różnych osób:

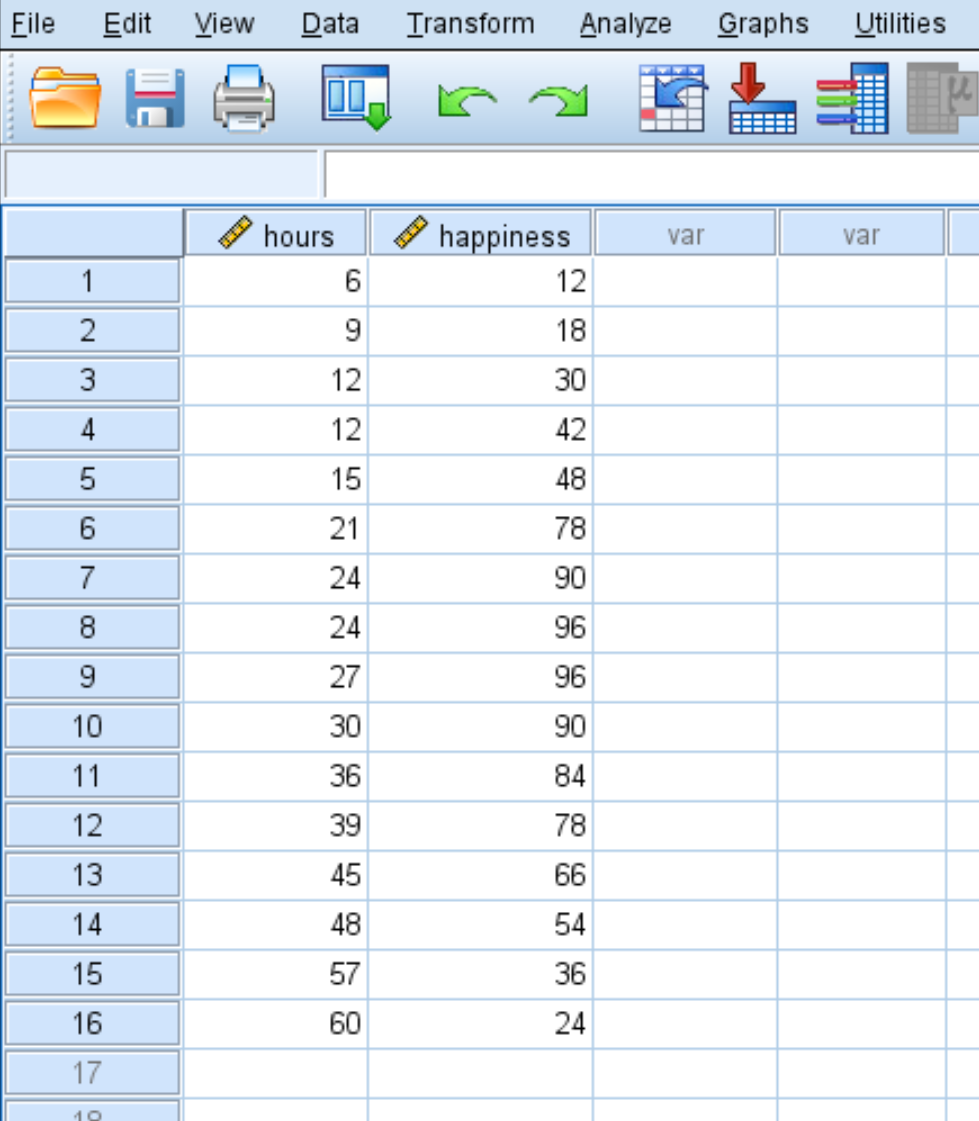
Wykonaj poniższe kroki, aby wykonać regresję kwadratową w SPSS.

Krok 1: Wizualizuj dane.

Przed wykonaniem regresji kwadratowej utwórzmy wykres rozrzutu, aby zwizualizować związek między przepracowanymi godzinami a szczęściem, aby sprawdzić, czy te dwie zmienne faktycznie mają związek kwadratowy.

Kliknij kartę Wykresy , a następnie kliknij opcję Kreator wykresów :

W nowym oknie, które się pojawi, wybierz opcję Scatter/Dot z listy Wybierz z . Następnie przeciągnij wykres oznaczony jako Simple Scatter do głównego okna edycji. Przeciągnij zmienne godziny na osi x i szczęście na osi y. Następnie kliknij OK .

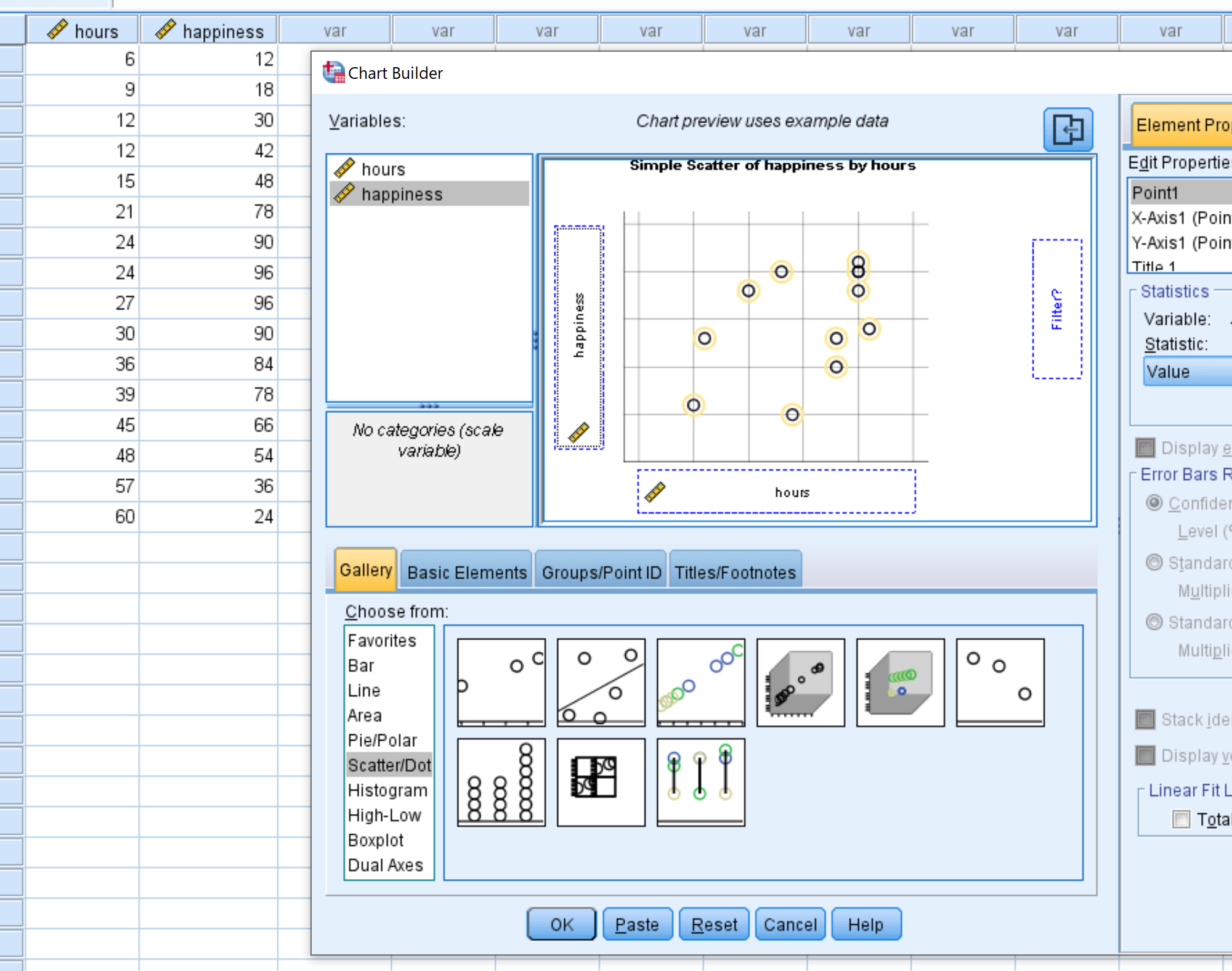
Pojawi się następujący wykres punktowy:

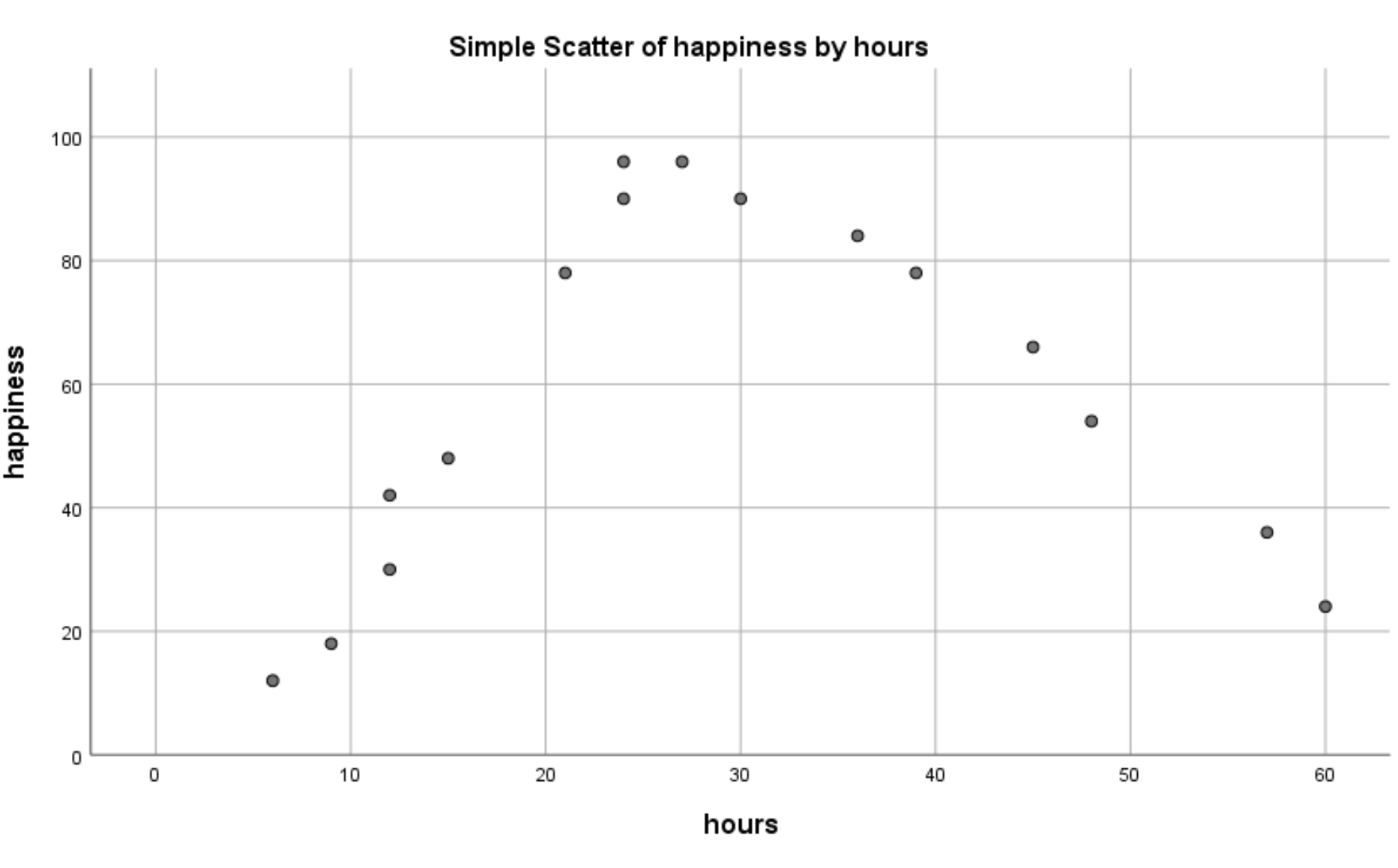
Wyraźnie widać, że istnieje nieliniowy związek pomiędzy przepracowanymi godzinami a szczęściem. To mówi nam, że regresja kwadratowa jest odpowiednią techniką do zastosowania w tej sytuacji.

Krok 2: Utwórz nową zmienną.

Zanim będziemy mogli przeprowadzić regresję kwadratową, musimy utworzyć zmienną predykcyjną dla godzin ² .

Kliknij kartę Transformacja , a następnie kliknij opcję Oblicz zmienną :

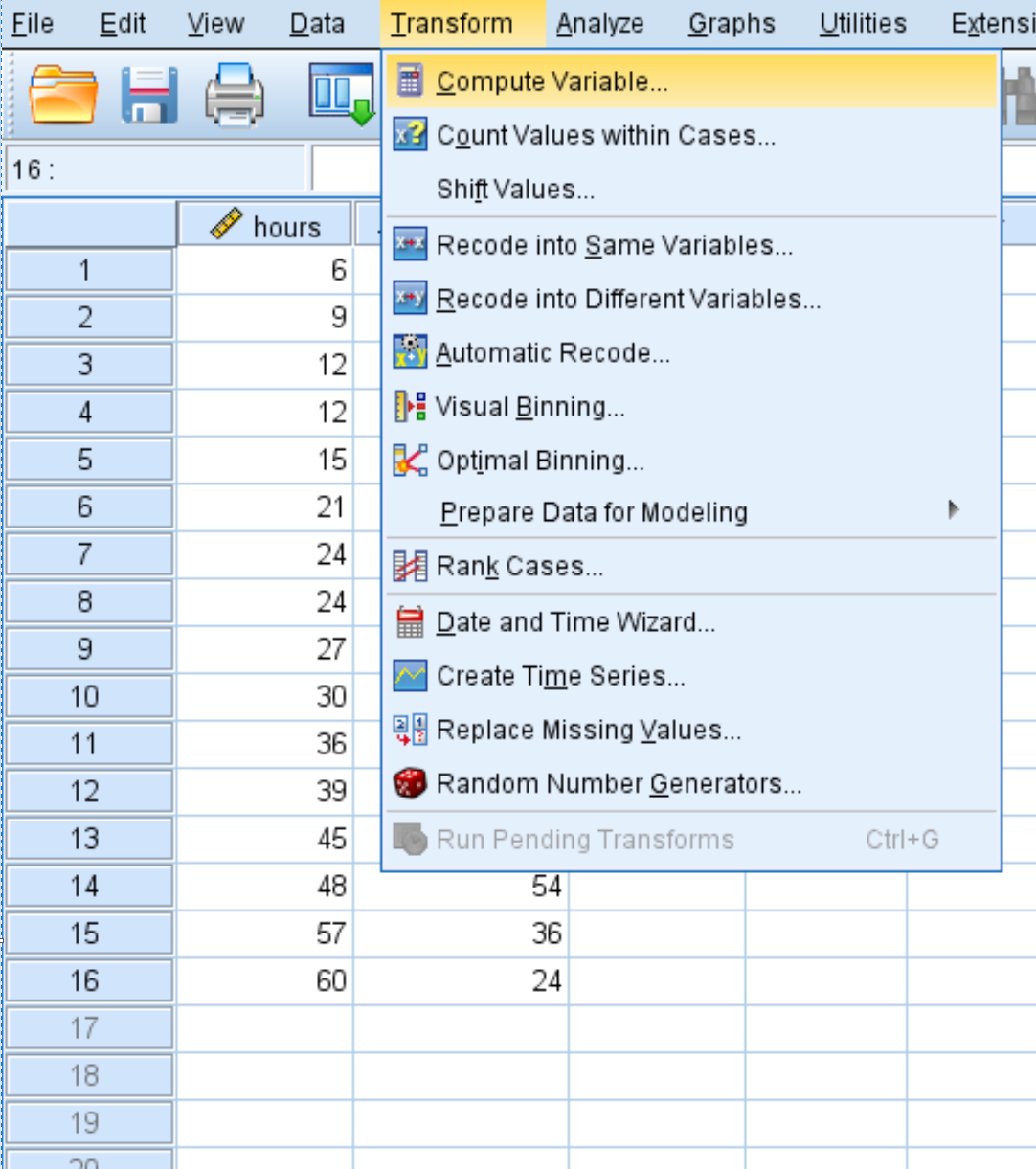
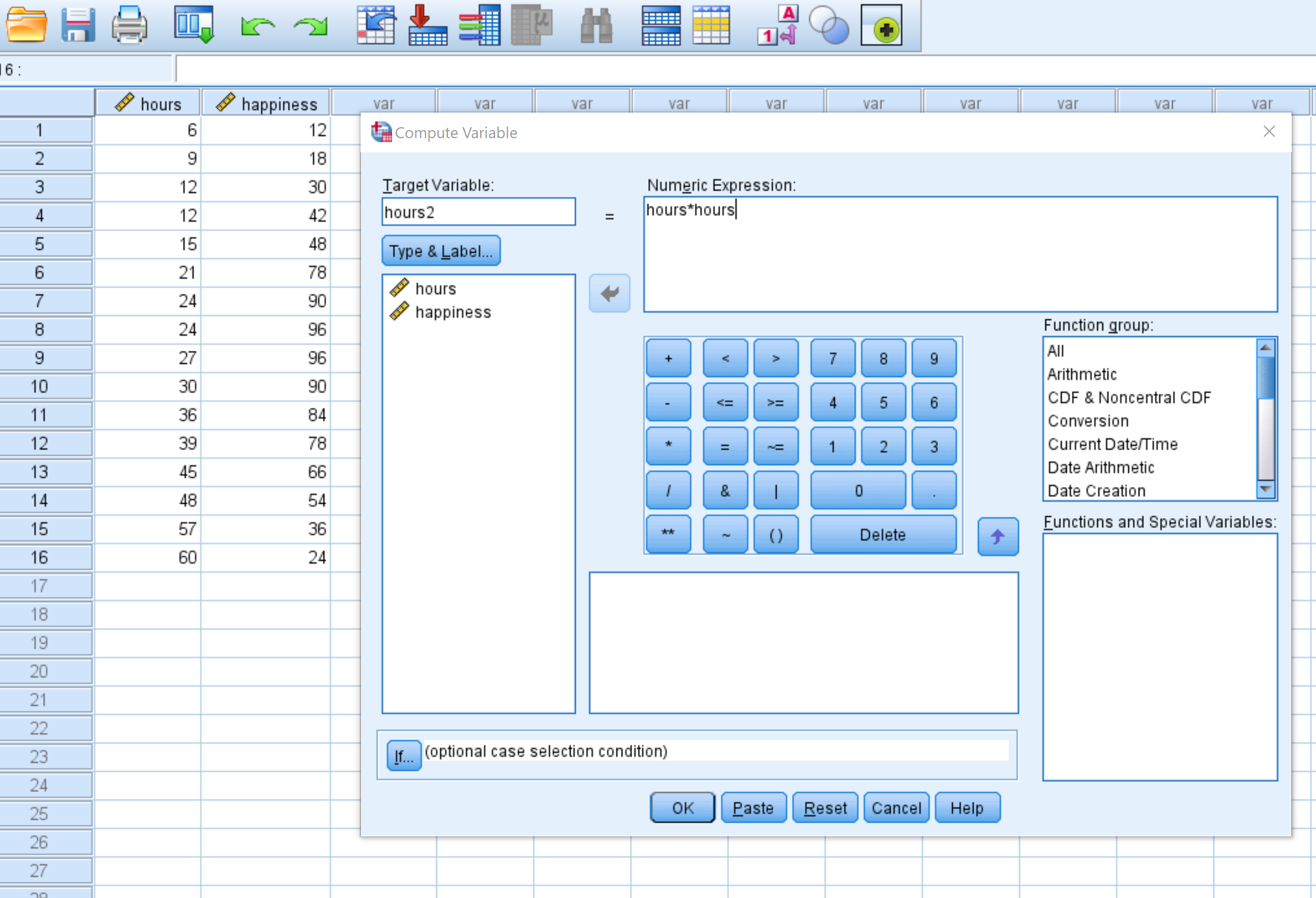
W nowym oknie, które się pojawi, nazwij zmienną docelową hours2 i ustaw ją na hours*hours :

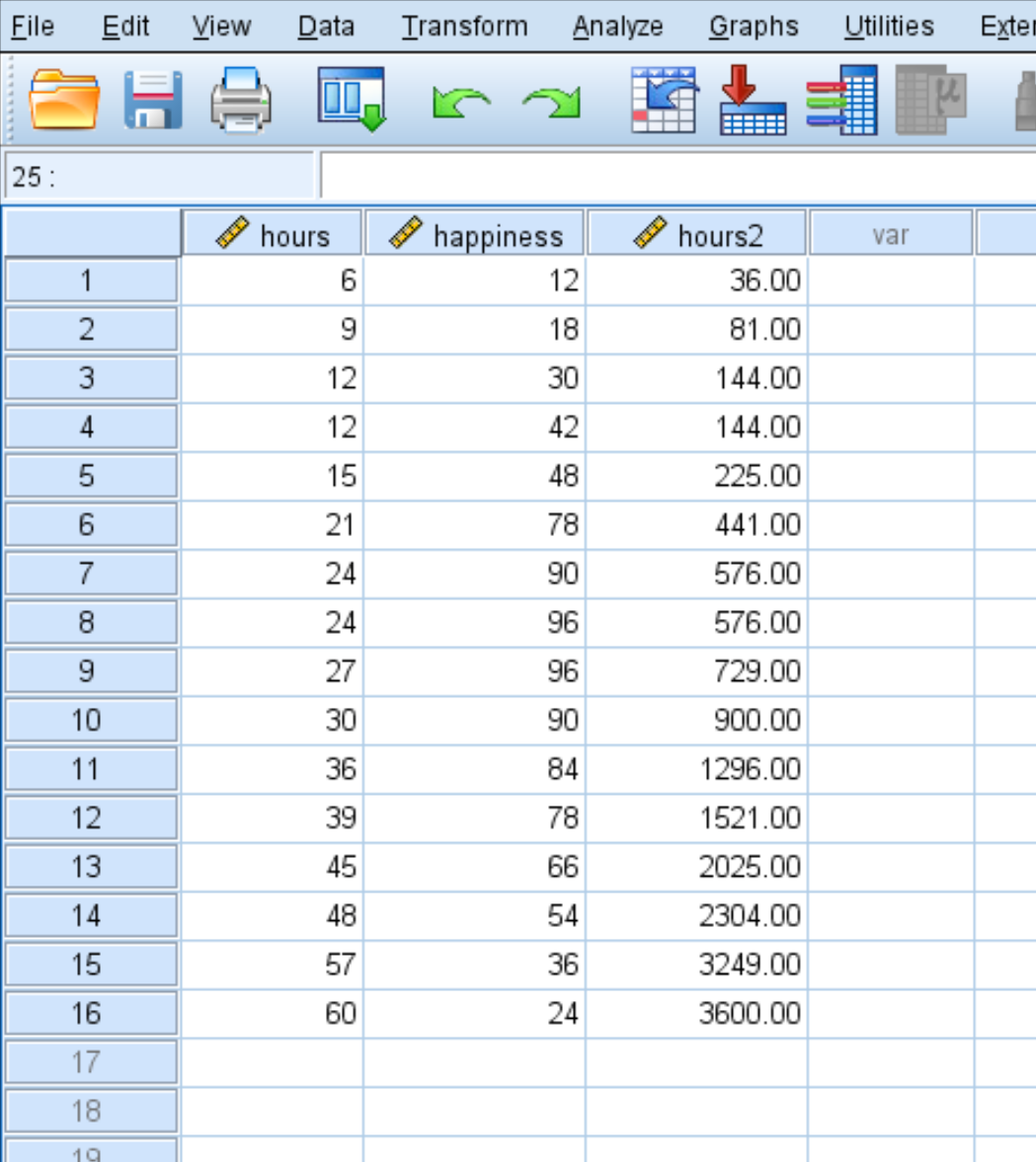
Po kliknięciu OK zmienna hours2 pojawi się w nowej kolumnie:

Krok 3: Wykonaj regresję kwadratową.

Następnie przeprowadzimy regresję kwadratową. Kliknij kartę Analiza , następnie Regresja , a następnie Liniowa :

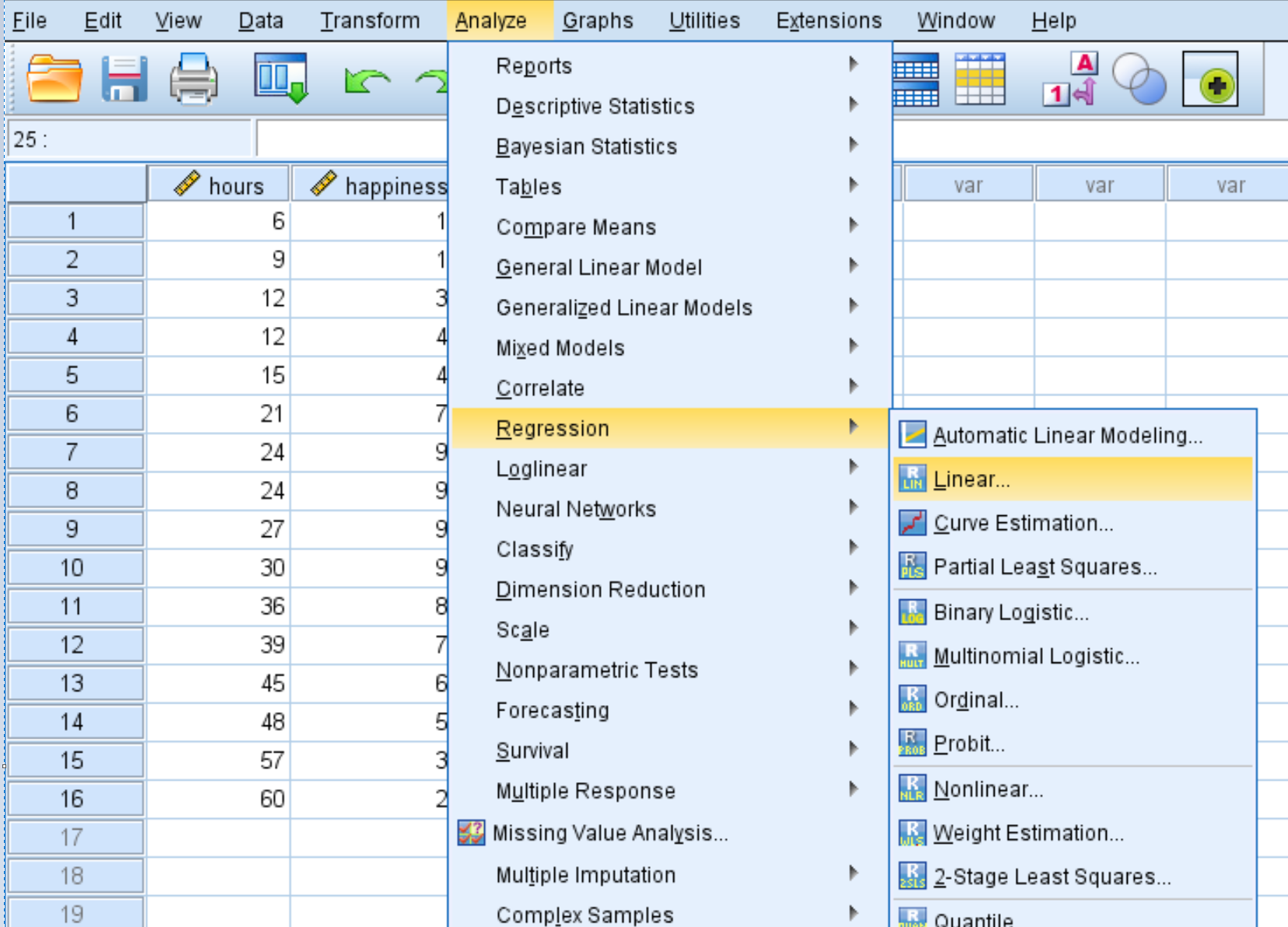
W nowym oknie, które się pojawi, przeciągnij szczęście do pola Zależne. Przeciągnij Godziny i Godziny2 do pola oznaczonego Niezależni. Następnie kliknij OK .

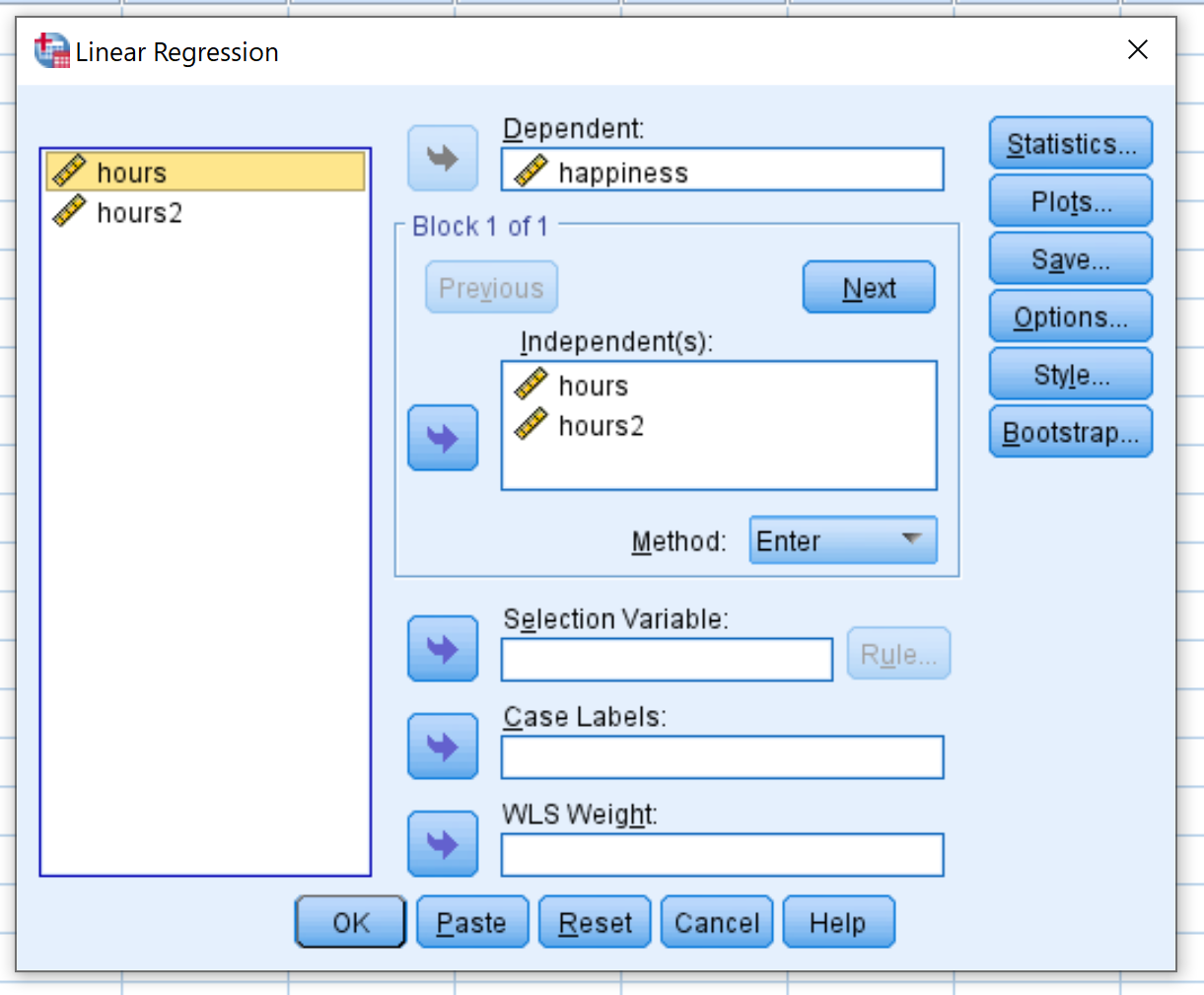
Krok 4: Interpretacja wyników.

Po kliknięciu OK wyniki regresji kwadratowej pojawią się w nowym oknie.

Pierwsza tabela, która nas interesuje, nazywa się Podsumowaniem modelu :

Oto jak interpretować najbardziej odpowiednie liczby w tej tabeli:

• Kwadrat R: Jest to proporcja wariancji zmiennej odpowiedzi, którą można wyjaśnić za pomocą zmiennych objaśniających. W tym przykładzie 90,9% zmienności szczęścia można wytłumaczyć godzinami i zmiennymi godzin ² .
• Standard. Błąd estymacji: błąd standardowy to średnia odległość pomiędzy obserwowanymi wartościami a linią regresji. W tym przykładzie zaobserwowane wartości odbiegają średnio o 9519 jednostek od linii regresji.

Następna tabela, która nas interesuje, nazywa się ANOVA :

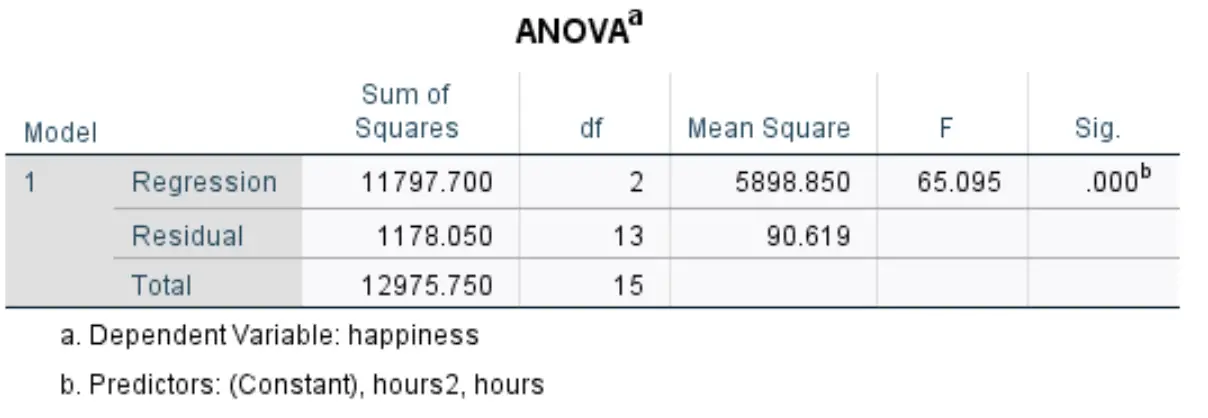
Oto jak interpretować najbardziej odpowiednie liczby w tej tabeli:

• F: Jest to ogólna statystyka F dla modelu regresji, obliczona jako regresja średniokwadratowa / reszta średniokwadratowa.
• Sig: Jest to wartość p powiązana z ogólną statystyką F. To mówi nam, czy model regresji jako całość jest statystycznie istotny, czy nie. W tym przypadku wartość p wynosi 0,000, co wskazuje, że zmienne objaśniające godziny i godziny ² łącznie mają statystycznie istotny związek z wynikiem egzaminu.

Poniższa tabela, która nas interesuje, nosi tytuł Współczynniki :

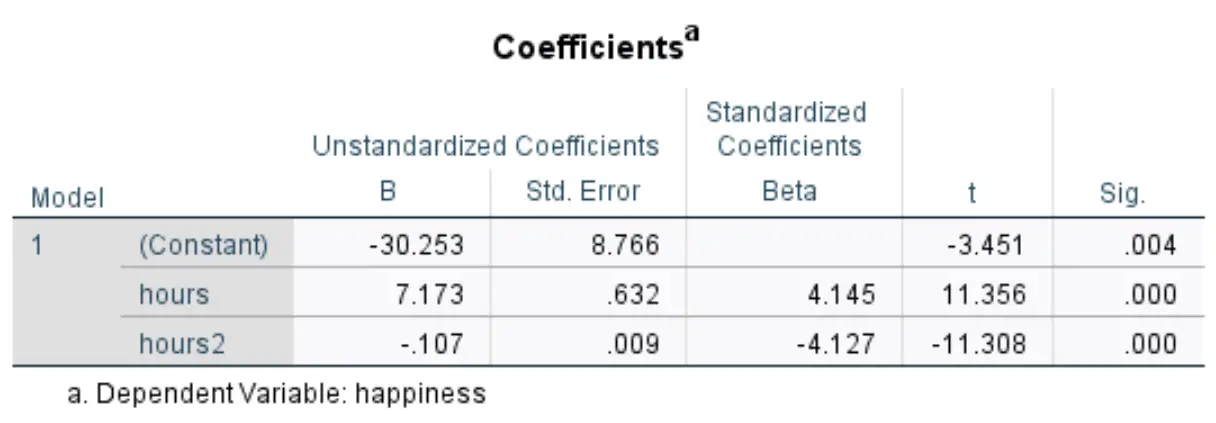
Możemy wykorzystać wartości z kolumny Niestandaryzowane B do utworzenia oszacowanego równania regresji dla tego zbioru danych:

Szacowany poziom szczęścia = -30,253 + 7,173*(godziny) – 0,107*(godziny ² )

Możemy użyć tego równania, aby znaleźć szacowany poziom szczęścia danej osoby na podstawie liczby godzin przepracowanych w tygodniu. Na przykład osoba pracująca 60 godzin tygodniowo powinna mieć poziom szczęścia 14,97:

Szacowany poziom szczęścia = -30,253 + 7,173*(60) – 0,107*(60 ² ) = 14,97 .

I odwrotnie, osoba pracująca 30 godzin tygodniowo powinna mieć poziom szczęścia na poziomie 88,65:

Szacowany poziom szczęścia = -30,253 + 7,173*(30) – 0,107*(30 ² ) = 88,65 .

Krok 5: Ogłoś wyniki.

Na koniec chcemy zgłosić wyniki naszej regresji kwadratowej. Oto przykład, jak to zrobić:

Przeprowadzono regresję kwadratową, aby określić ilościowo związek między liczbą godzin przepracowanych przez daną osobę a odpowiadającym jej poziomem szczęścia (mierzonym od 0 do 100). Do analizy wykorzystano próbę 16 osób.

Wyniki wykazały, że istnieje istotna statystycznie zależność pomiędzy zmiennymi objaśniającymi godziny i godziny ² a zmienną odpowiedzi szczęście (F(2, 13) = 65,095, p < 0,000).

Razem te dwie zmienne objaśniające odpowiadały za 90,9% zmienności szczęścia.

Równanie regresji okazało się następujące:

Szacowany poziom szczęścia = -30,253 + 7,173 (godziny) – 0,107 ( ² godziny)