Jak wykonać test niezależności chi-kwadrat w spss
Test niezależności chi-kwadrat służy do określenia, czy istnieje istotny związek między dwiema zmiennymi kategorycznymi.
W tym samouczku wyjaśniono, jak przeprowadzić test niezależności chi-kwadrat w SPSS.
Przykład: Test niezależności chi-kwadrat w SPSS
Załóżmy, że chcemy wiedzieć, czy płeć jest powiązana z preferencją partii politycznej. Bierzemy prostą losową próbę 500 wyborców i pytamy ich o preferencje dotyczące partii politycznych. Wyniki badania prezentuje poniższa tabela:
| Republikański | Demokrata | Niezależny | Całkowity | |
| Mężczyzna | 120 | 90 | 40 | 250 |
| Kobieta | 110 | 95 | 45 | 250 |
| Całkowity | 230 | 185 | 85 | 500 |
Wykonaj poniższe kroki, aby wykonać test niezależności chi-kwadrat w SPSS w celu ustalenia, czy płeć jest powiązana z preferencjami partii politycznych.
Krok 1: Wprowadź dane.
Najpierw wprowadź dane w następującym formacie:
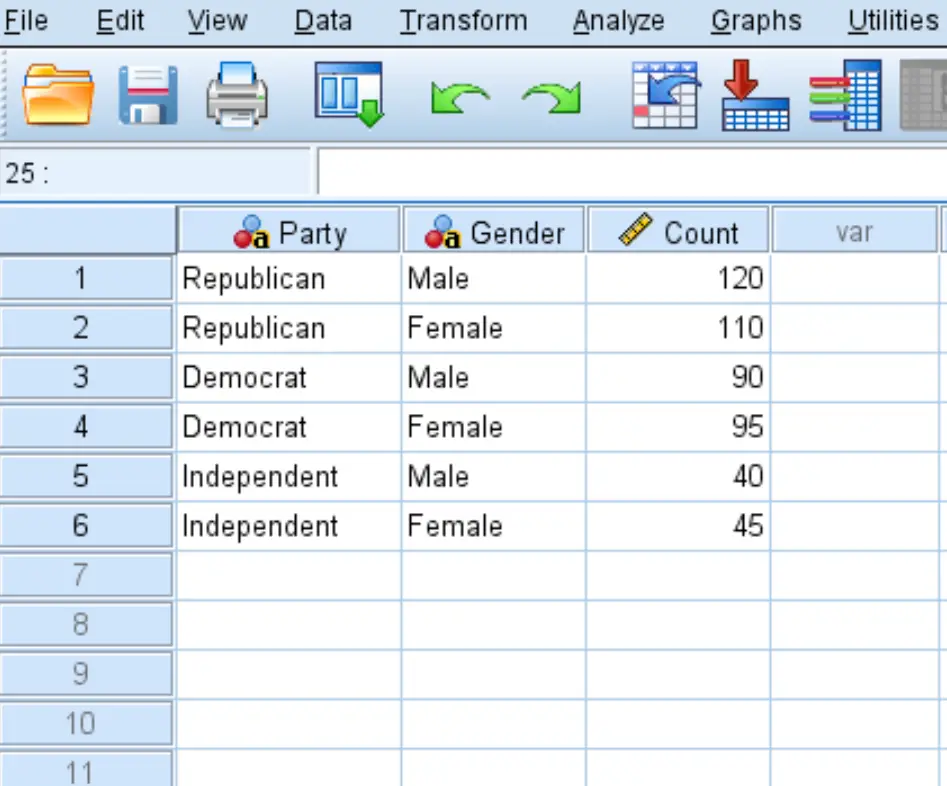
Krok 2: Użyj ważonych pudełek.
Aby test działał poprawnie, musimy poinformować SPSS, że zmienne Party i Płeć powinny być ważone zmienną Count.
Kliknij kartę Dane , a następnie opcję Przypadki wagowe :
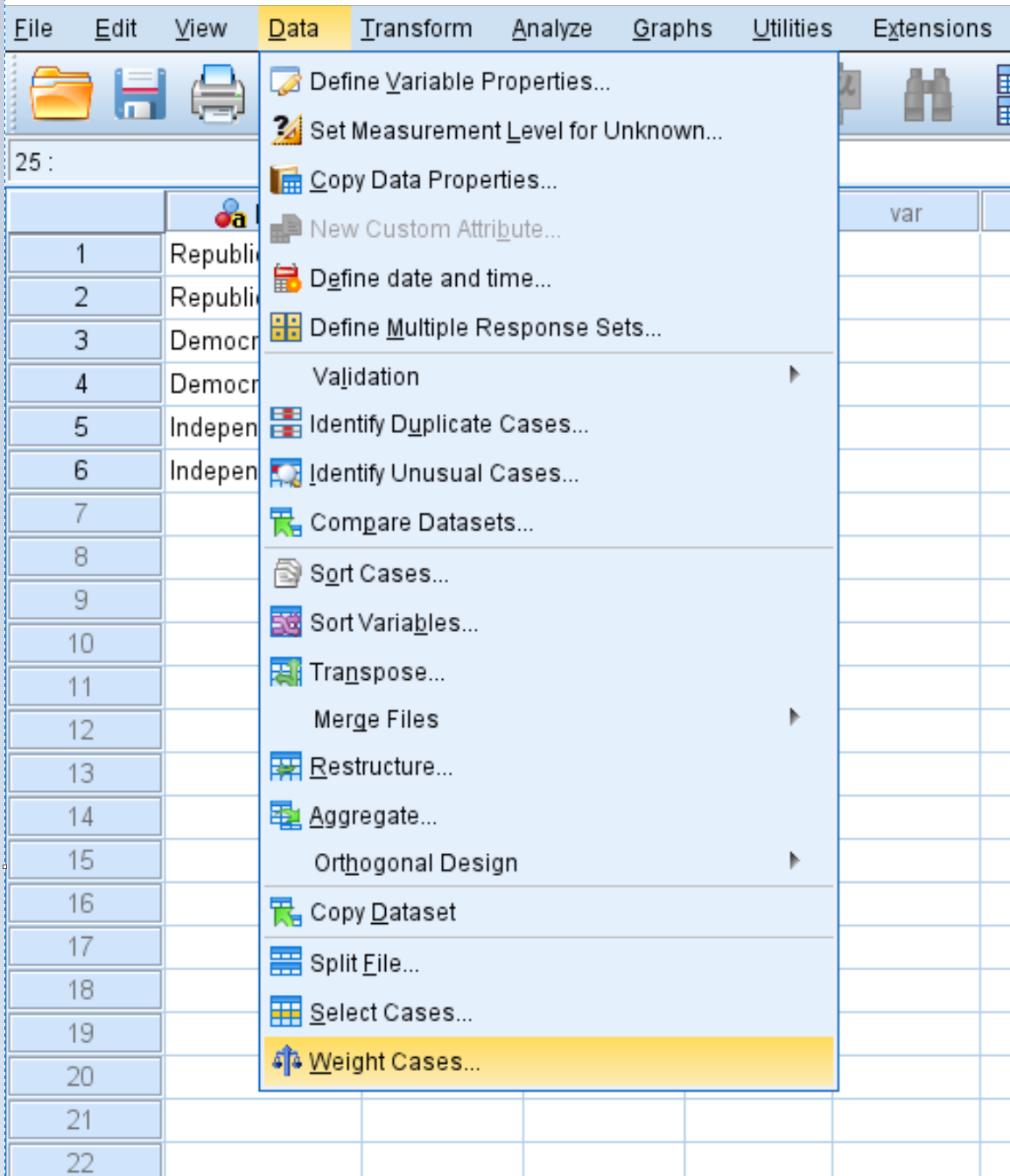
W nowym oknie, które się pojawi, przeciągnij zmienną Count do obszaru oznaczonego Lista zmiennych testowych. Następnie kliknij OK .
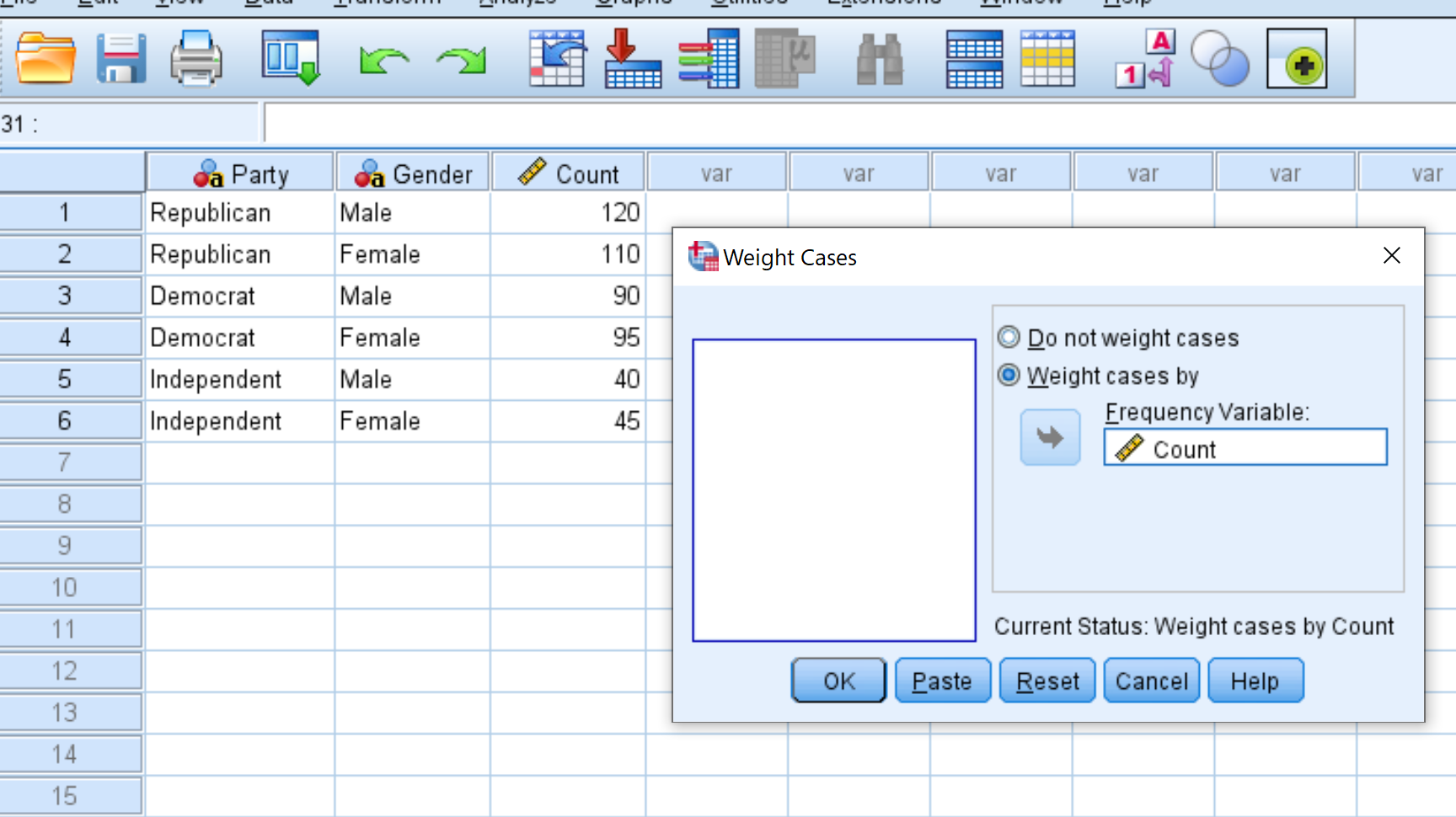
Krok 3: Wykonaj test dobroci dopasowania chi-kwadrat.
Kliknij kartę Analiza , następnie Statystyki opisowe i Tabele przestawne :
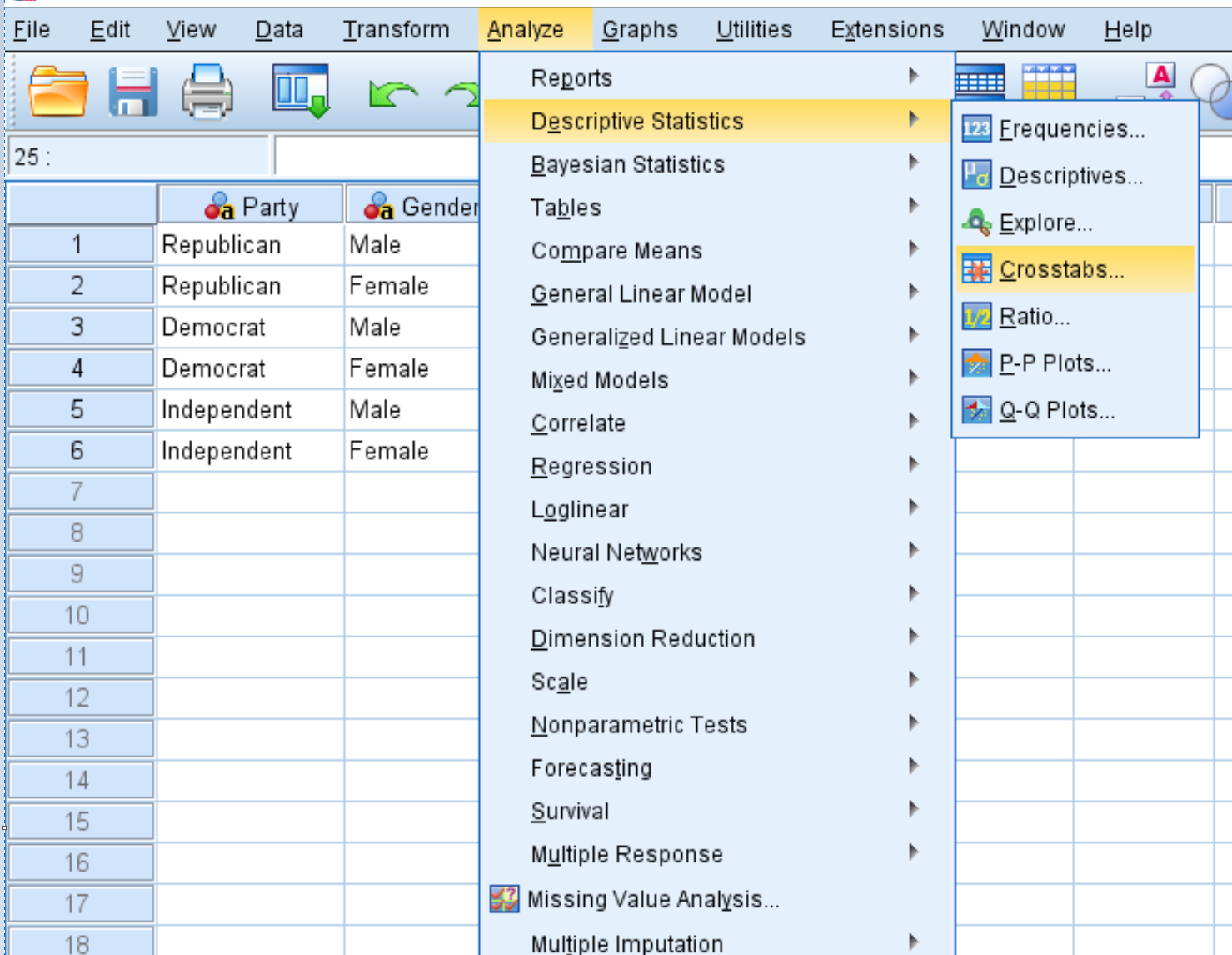
W nowym oknie, które się pojawi, przeciągnij zmienną Gatunek do obszaru o nazwie Wiersze, a zmienną Część do obszaru o nazwie Kolumny. Następnie kliknij Statystyki i upewnij się, że pole obok Chi Square jest zaznaczone. KliknijKontynuuj . Następnie kliknij OK .
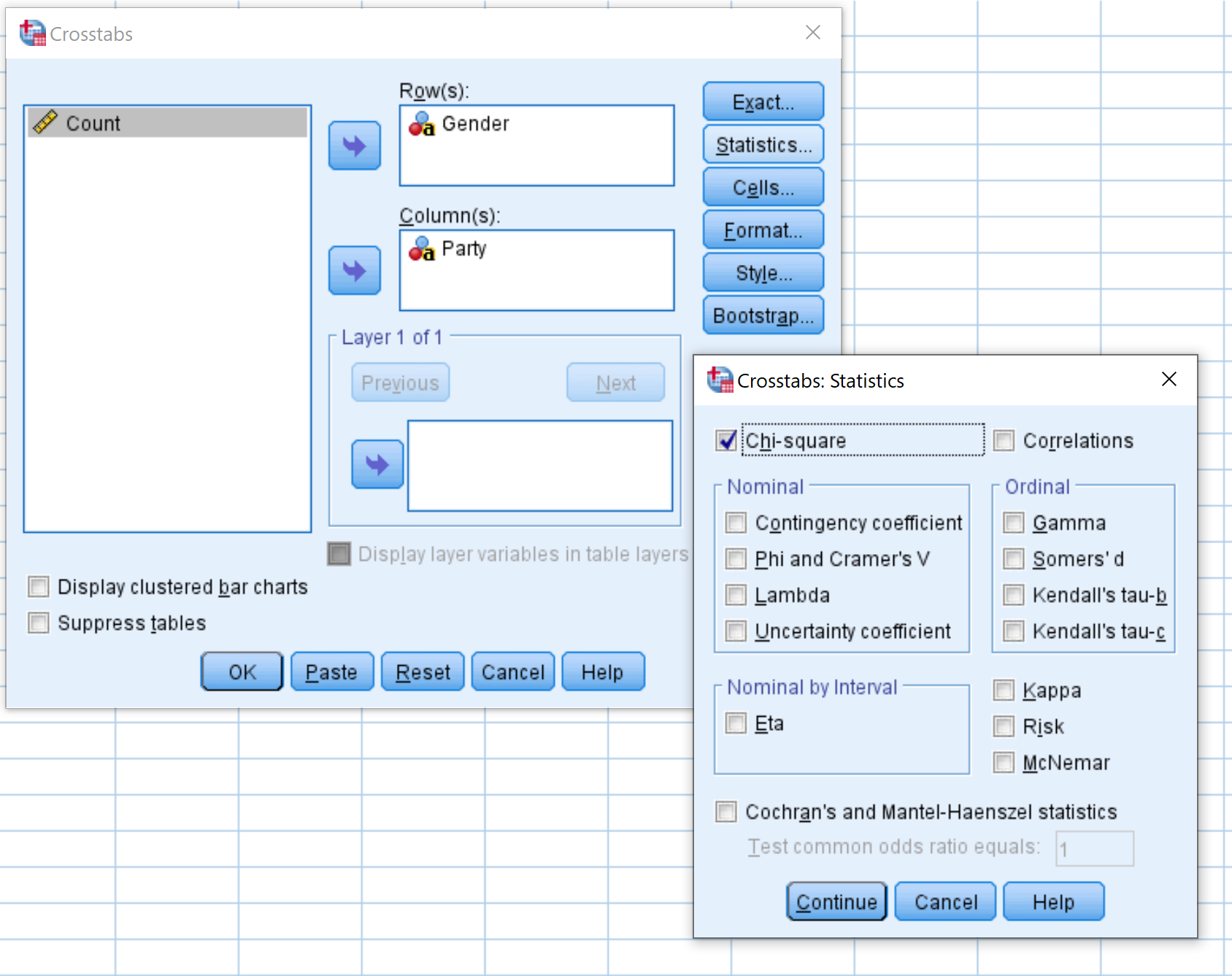
Krok 4: Interpretacja wyników .
Po kliknięciu OK pojawią się wyniki testu niezależności chi-kwadrat:
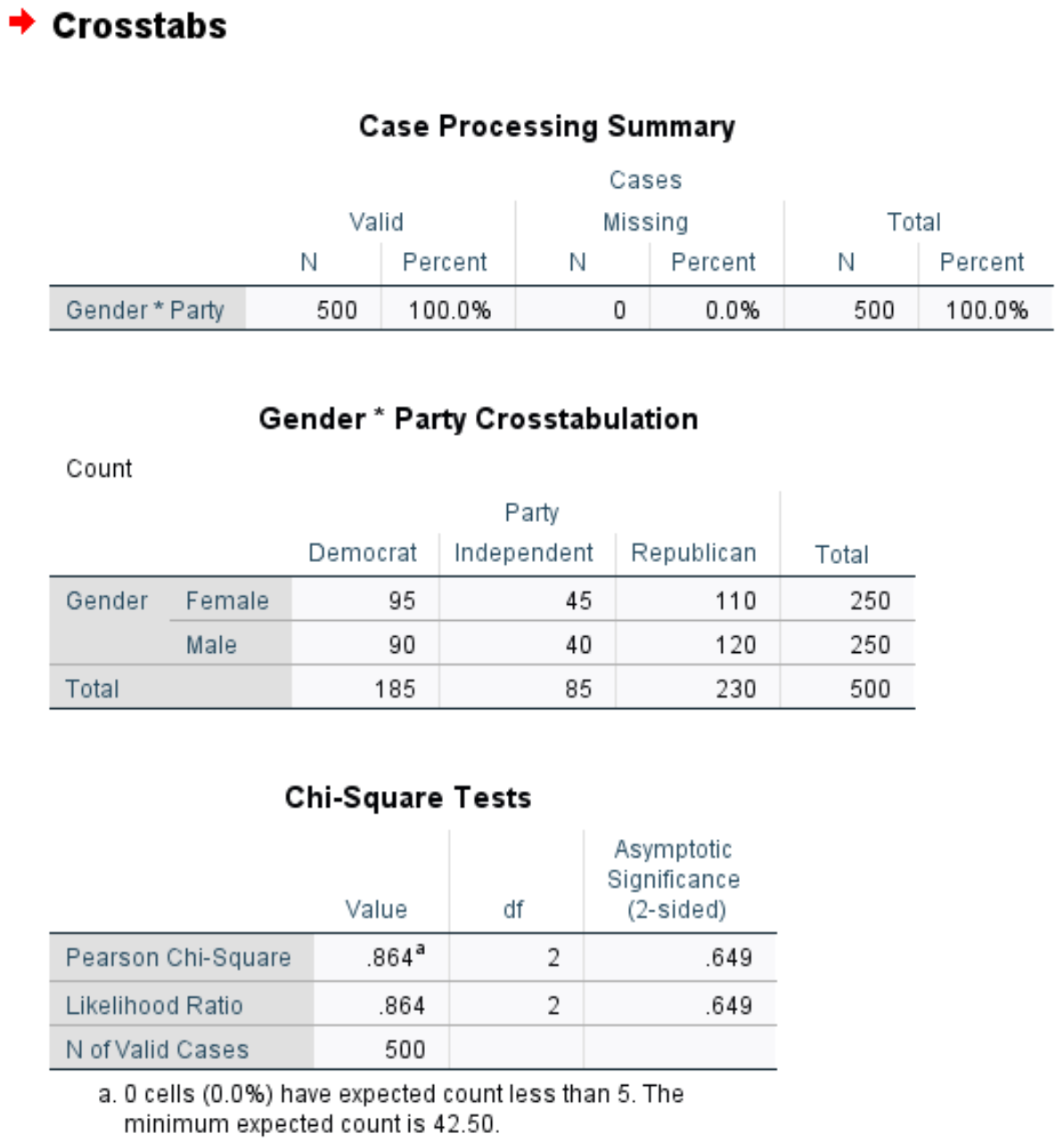
Pierwsza tabela wyświetla liczbę brakujących obserwacji w zbiorze danych. Widzimy, że w tym przykładzie brakuje 0 przypadków.
Druga tabela przedstawia tabelę krzyżową całkowitej liczby osób według płci i preferencji partii politycznych.
Trzecia tabela przedstawia wyniki testu niezależności chi-kwadrat. Statystyka testowa wynosi 0,864 , a odpowiadająca jej dwustronna wartość p wynosi 0,649 .
Hipotezą zerową testu niezależności chi-kwadrat jest to, że obie zmienne są niezależne. W tym przypadku naszą hipotezą zerową jest to, że preferencje dotyczące płci i partii politycznych są niezależne.
Ponieważ wartość p (0,649) testu jest nie mniejsza niż 0,05, nie możemy odrzucić hipotezy zerowej.
Oznacza to, że nie mamy wystarczających dowodów, aby stwierdzić, że istnieje związek między płcią a preferencjami partii politycznych.