Jak utworzyć i zinterpretować krzywą roc w spss

Regresja logistyczna to metoda statystyczna, której używamy do dopasowania modelu regresji, gdy zmienna odpowiedzi jest binarna. Aby ocenić, jak dobrze model regresji logistycznej pasuje do zbioru danych, możemy przyjrzeć się następującym dwóm metrykom:

• Czułość: prawdopodobieństwo, że model przewiduje pozytywny wynik obserwacji, gdy wynik jest rzeczywiście pozytywny.
• Specyfika: prawdopodobieństwo, że model przewiduje negatywny wynik obserwacji, gdy wynik jest faktycznie negatywny.

Prostym sposobem wizualizacji tych dwóch metryk jest utworzenie krzywej ROC , czyli wykresu przedstawiającego czułość i swoistość modelu regresji logistycznej.

W tym samouczku wyjaśniono, jak utworzyć i zinterpretować krzywą ROC w SPSS.

Przykład: krzywa ROC w SPSS

Załóżmy, że mamy następujący zestaw danych, który pokazuje, czy koszykarz został powołany do NBA (0 = nie, 1 = tak), a także jego średnią punktów na mecz w college’u:

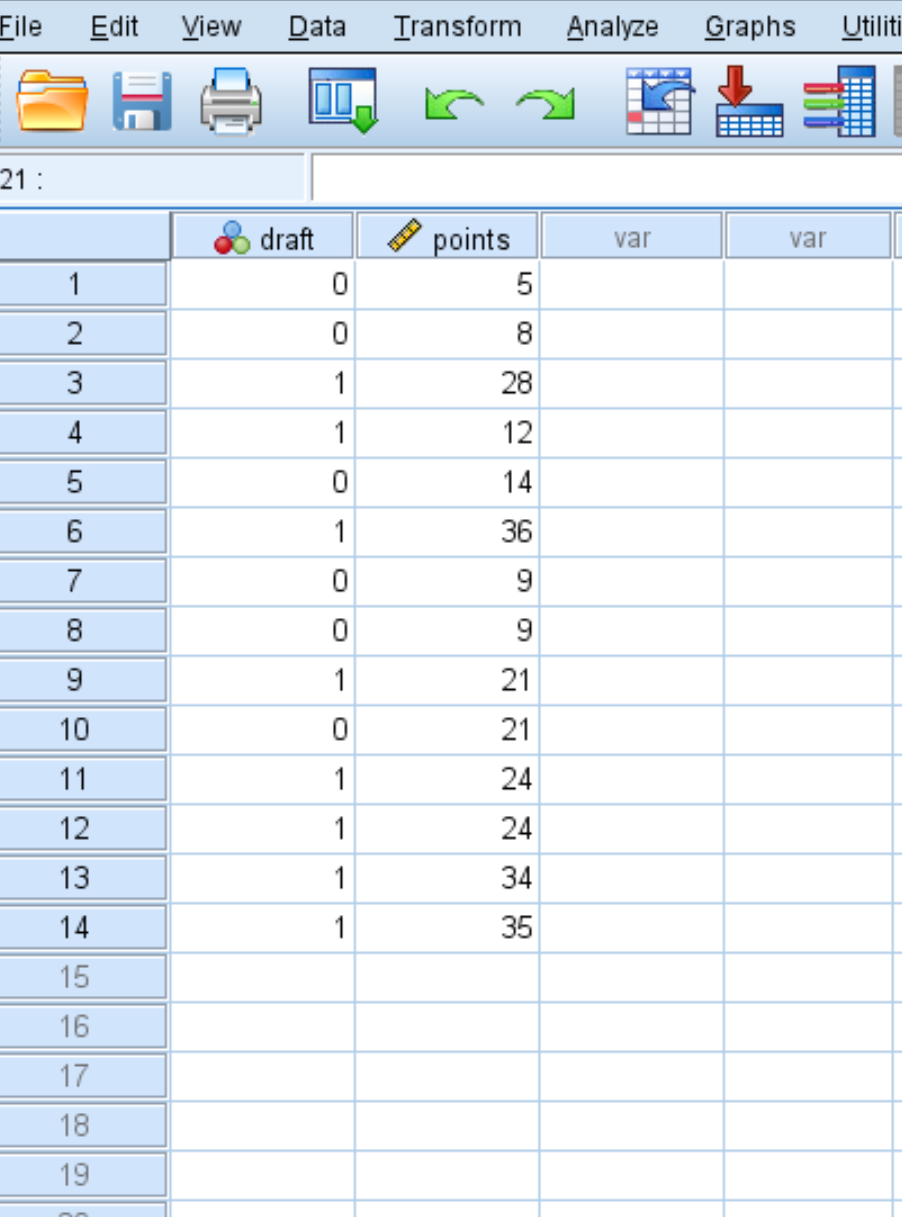
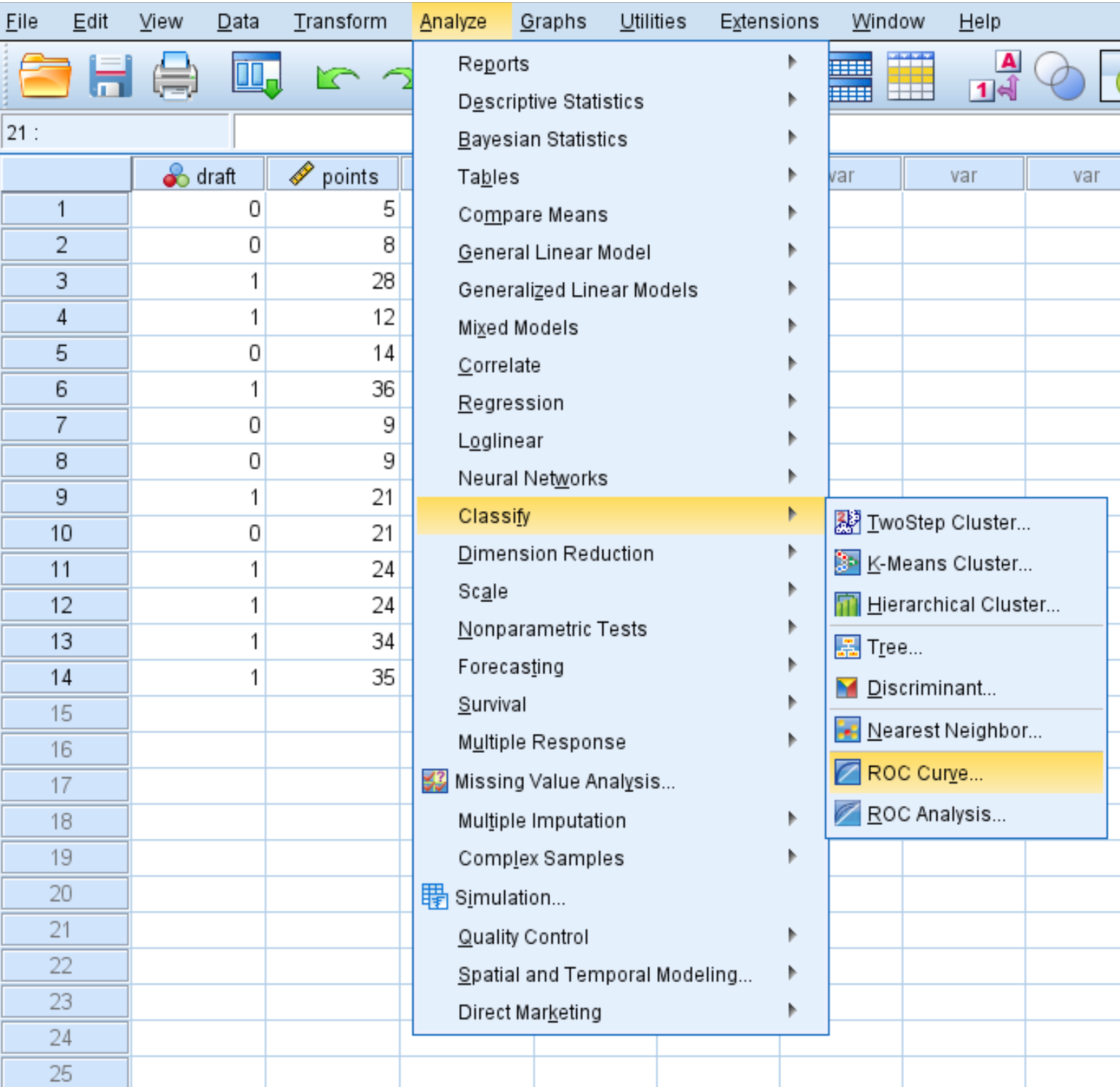
Aby utworzyć krzywą ROC dla tego zbioru danych, kliknij kartę Analizuj , następnie Klasyfikuj , a następnie Krzywa ROC :

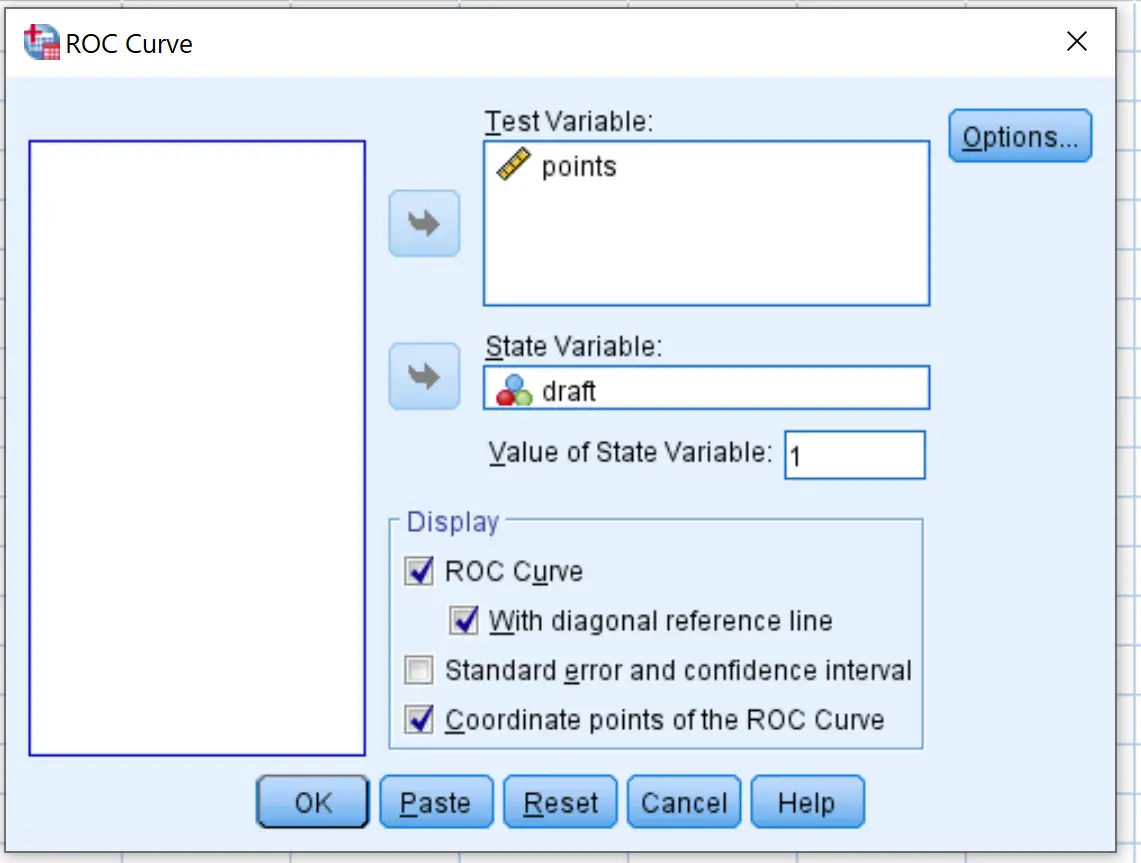
W nowym oknie, które się pojawi, przeciągnij zmienną roboczą do obszaru oznaczonego Zmienna stanu. Ustaw wartość zmiennej stanu na 1 . (Jest to wartość wskazująca, że gracz został wybrany). Przeciągnij punkty zmienne do obszaru oznaczonego Zmienna testowa.

Zaznacz pola obok Z ukośną linią odniesienia i współrzędnymi punktu krzywej ROC . Następnie kliknij OK .

Oto jak zinterpretować wynik:

Podsumowanie przetwarzania plików:

W tej tabeli wyświetlana jest łączna liczba obserwacji dodatnich i ujemnych w zbiorze danych. W tym przykładzie 8 graczy zostało powołanych (wynik pozytywny), a 6 graczy nie zostało powołanych (wynik negatywny):

Krzywa ROC:

Krzywa charakterystyki działania odbiornika (ROC) to wykres wartości czułości w funkcji specyficzności 1, gdy wartość progowa zmienia się z 0 na 1:

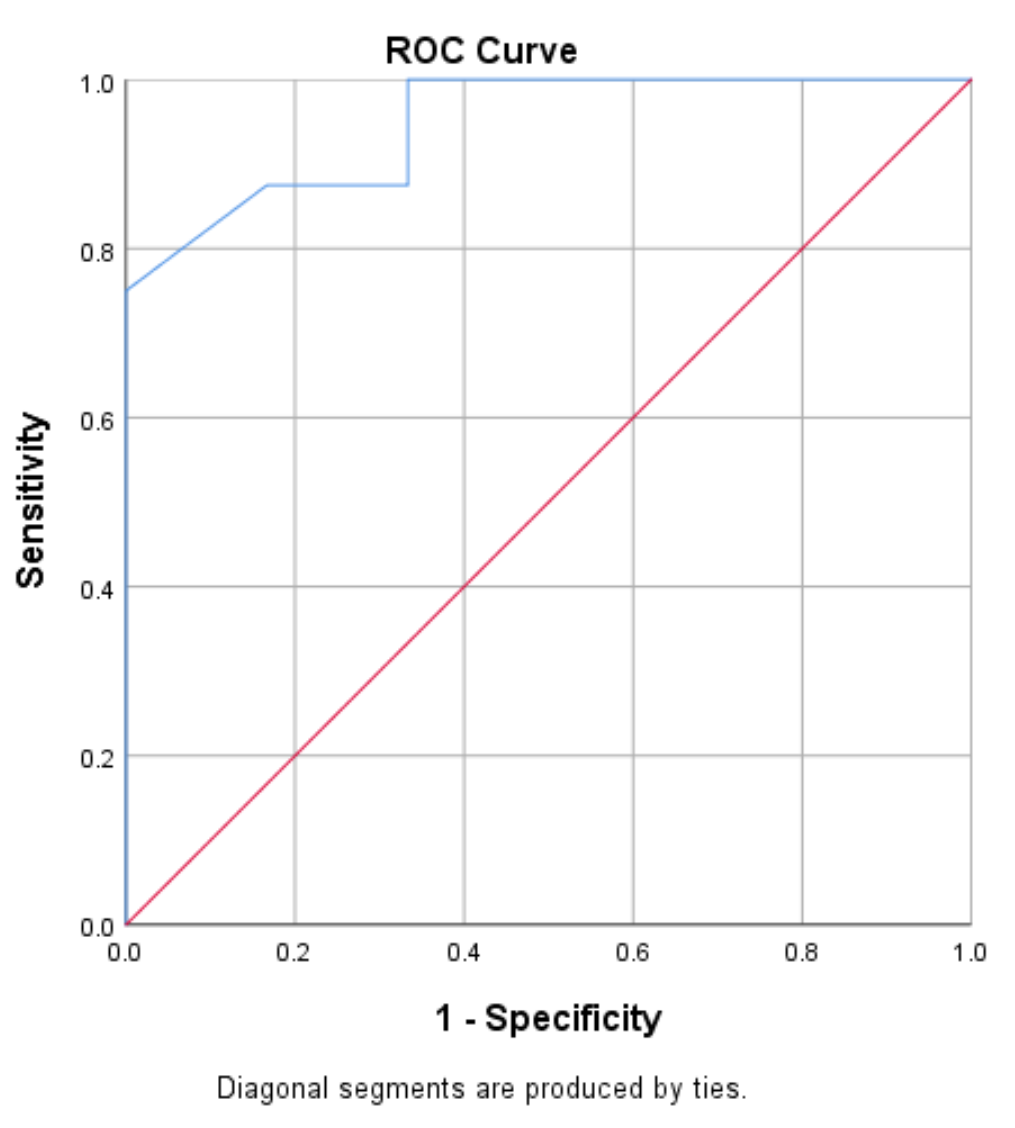
Model o wysokiej czułości i swoistości będzie miał krzywą ROC pasującą do lewego górnego rogu wykresu. Model o niskiej czułości i niskiej swoistości będzie miał krzywą zbliżoną do przekątnej 45 stopni.

Widzimy, że krzywa ROC (niebieska linia) w tym przykładzie obejmuje lewy górny róg wykresu, co wskazuje, że model dobrze radzi sobie z przewidywaniem, czy gracze zostaną powołani do draftu, czy nie, na podstawie ich średniej liczby punktów na mecz . .

Pole pod krzywą:

Pole pod krzywą daje nam wyobrażenie o zdolności modelu do rozróżnienia wyników pozytywnych i negatywnych. AUC może mieścić się w zakresie od 0 do 1. Im wyższe AUC, tym lepiej model poprawnie klasyfikuje wyniki.

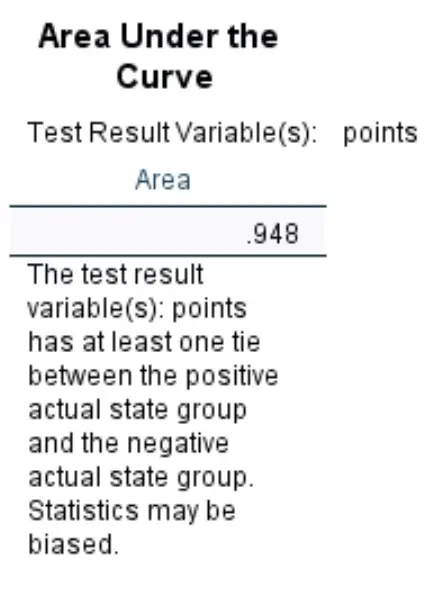
Widzimy, że AUC dla tego konkretnego modelu regresji logistycznej wynosi 0,948 , co jest niezwykle wysoką wartością. Oznacza to, że model dobrze radzi sobie z przewidywaniem, czy zawodnik zostanie wybrany, czy nie.

Współrzędne krzywej:

Ta ostatnia tabela przedstawia czułość i swoistość 1 krzywej ROC dla różnych progów.

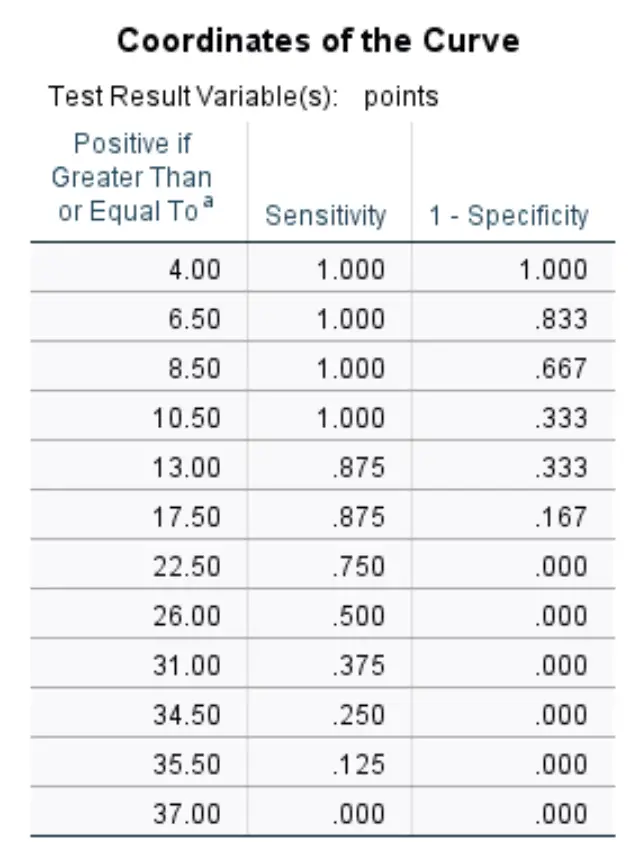
Na przykład:

Jeśli przyjmiemy, że próg wynosi 8,50 , oznacza to, że spodziewamy się, że każdy gracz, który zdobędzie mniej niż 8,50 punktów na mecz, nie zostanie wybrany, a każdy gracz, który zdobędzie więcej niż 8,50 punktów na mecz, zostanie wybrany.

Przyjmując to jako próg, nasza czułość wyniosłaby 100% (ponieważ każdy gracz, który zdobył mniej niż 8,50 punktów na mecz rzeczywiście nie został wybrany), a nasza specyfika 1 wyniosłaby 66,7% (ponieważ 8 z 12 graczy, którzy zdobyli więcej niż 8,50 punktów na mecz został wybrany).

Powyższa tabela pozwala nam zobaczyć czułość i swoistość 1 dla każdego potencjalnego progu.