Jak utworzyć macierz kowariancji w pythonie
Kowariancja jest miarą tego, jak zmiany jednej zmiennej są powiązane ze zmianami drugiej zmiennej. Mówiąc dokładniej, jest to miara stopnia, w jakim dwie zmienne są liniowo powiązane.
Macierz kowariancji to macierz kwadratowa, która pokazuje kowariancję pomiędzy wieloma różnymi zmiennymi. Może to być przydatny sposób zrozumienia, w jaki sposób różne zmienne są powiązane w zbiorze danych.
Poniższy przykład pokazuje, jak utworzyć macierz kowariancji w Pythonie.
Jak utworzyć macierz kowariancji w Pythonie
Wykonaj poniższe kroki, aby utworzyć macierz kowariancji w Pythonie.
Krok 1: Utwórz zbiór danych.
Najpierw utworzymy zbiór danych zawierający wyniki testów 10 różnych uczniów z trzech przedmiotów: matematyki, nauk ścisłych i historii.
import numpy as np math = [84, 82, 81, 89, 73, 94, 92, 70, 88, 95] science = [85, 82, 72, 77, 75, 89, 95, 84, 77, 94] history = [97, 94, 93, 95, 88, 82, 78, 84, 69, 78] data = np.array([math, science, history])
Krok 2: Utwórz macierz kowariancji.
Następnie utworzymy macierz kowariancji dla tego zbioru danych za pomocą funkcji numpy cov() , określając, że odchylenie = True , abyśmy mogli obliczyć macierz kowariancji populacji.
np.cov(data, bias= True )
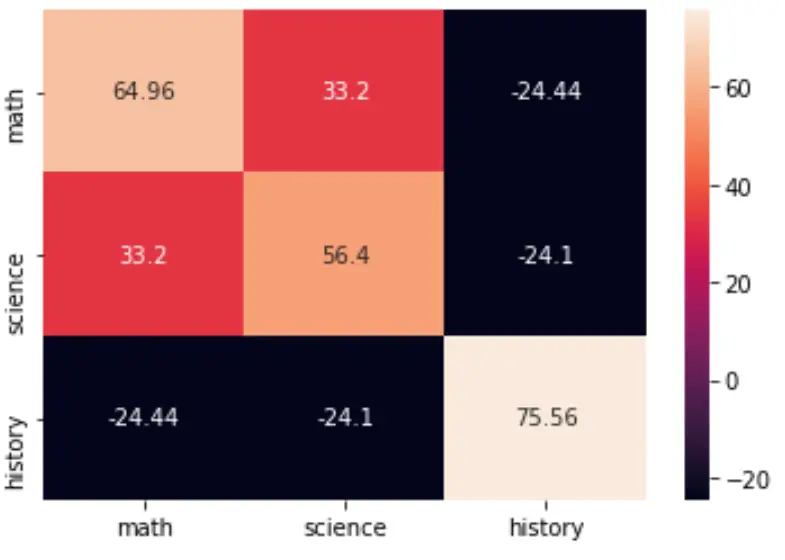
array([[ 64.96, 33.2, -24.44],
[33.2, 56.4, -24.1],
[-24.44, -24.1, 75.56]])
Krok 3: Interpretacja macierzy kowariancji.
Wartości wzdłuż przekątnych macierzy są po prostu wariancjami każdego przedmiotu. Na przykład:
- Wariancja wyników z matematyki wynosi 64,96
- Wariancja wyników z przedmiotów ścisłych wynosi 56,4
- Historyczna wariancja wyniku wynosi 75,56
Pozostałe wartości macierzy reprezentują kowariancje pomiędzy różnymi podmiotami. Na przykład:
- Kowariancja między wynikami z matematyki i przedmiotów ścisłych wynosi 33,2.
- Kowariancja między wynikami z matematyki i historii wynosi -24,44.
- Kowariancja między wynikami z nauk ścisłych i historii wynosi -24,1.
Dodatnia liczba kowariancji wskazuje, że dwie zmienne mają tendencję do wzrostu lub spadku w tandemie. Na przykład matematyka i przedmioty ścisłe mają dodatnią kowariancję (33,2), co wskazuje, że uczniowie, którzy uzyskują wysokie wyniki z matematyki, zwykle osiągają wysokie wyniki w przedmiotach ścisłych. I odwrotnie, uczniowie, którzy osiągają słabe wyniki w matematyce, zwykle osiągają słabe wyniki w naukach ścisłych.
Ujemna liczba kowariancji wskazuje, że w miarę wzrostu jednej zmiennej druga zmienna ma tendencję do zmniejszania się. Na przykład matematyka i historia mają ujemną kowariancję (-24,44), co wskazuje, że uczniowie, którzy uzyskują wysokie wyniki z matematyki, zwykle osiągają niskie wyniki z historii. I odwrotnie, uczniowie, którzy osiągają niskie wyniki z matematyki, zwykle osiągają wysokie wyniki z historii.
Krok 4: Wizualizuj macierz kowariancji (opcjonalnie).
Możesz wizualizować macierz kowariancji za pomocą funkcji heatmap() pakietu seaborn:
import seaborn as sns import matplotlib.pyplot as plt cov = np.cov(data, bias=True) labs = ['math', 'science', 'history'] sns.heatmap(cov, annot=True, fmt='g', xticklabels=labs, yticklabels=labs) plt.show()
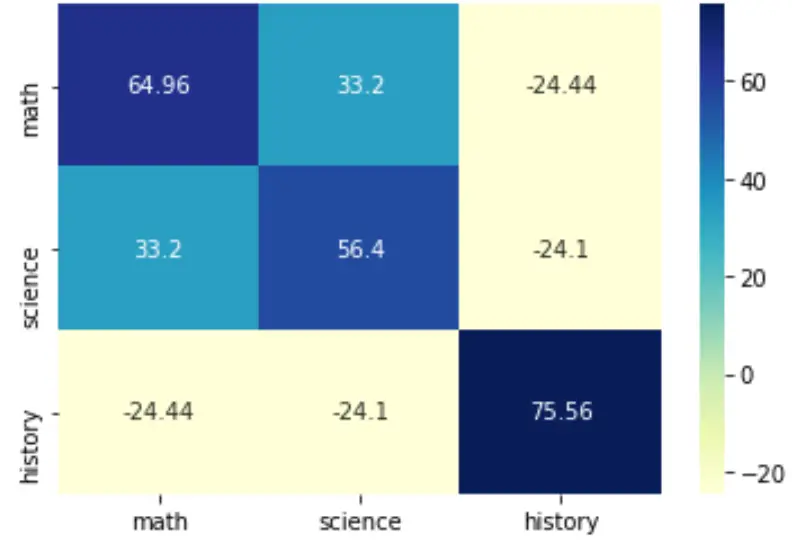
Możesz także zmienić paletę kolorów, podając argument cmap :
sns.heatmap(cov, annot=True, fmt='g', xticklabels=labs, yticklabels=labs, cmap=' YlGnBu ')
plt.show()
Aby uzyskać więcej informacji na temat stylizacji tej mapy cieplnej, zapoznaj się z dokumentacją seaborn .