Jak utworzyć wykres resztkowy w pythonie
Wykres reszt to rodzaj wykresu, na którym wyświetlane są dopasowane wartości względem reszt modelu regresji .
Ten typ wykresu jest często używany do oceny, czy model regresji liniowej jest odpowiedni dla danego zbioru danych, oraz do sprawdzenia reszt pod kątem heteroskedastyczności .
W tym samouczku wyjaśniono, jak utworzyć wykres reszt dla modelu regresji liniowej w języku Python.
Przykład: wykres resztkowy w Pythonie
W tym przykładzie użyjemy zbioru danych opisującego atrybuty 10 koszykarzy:
import numpy as np import pandas as pd #create dataset df = pd.DataFrame({'rating': [90, 85, 82, 88, 94, 90, 76, 75, 87, 86], 'points': [25, 20, 14, 16, 27, 20, 12, 15, 14, 19], 'assists': [5, 7, 7, 8, 5, 7, 6, 9, 9, 5], 'rebounds': [11, 8, 10, 6, 6, 9, 6, 10, 10, 7]}) #view dataset df rating points assists rebounds 0 90 25 5 11 1 85 20 7 8 2 82 14 7 10 3 88 16 8 6 4 94 27 5 6 5 90 20 7 9 6 76 12 6 6 7 75 15 9 10 8 87 14 9 10 9 86 19 5 7
Wykres reszt dla prostej regresji liniowej
Załóżmy, że dopasowujemy prosty model regresji liniowej, wykorzystując punkty jako zmienną predykcyjną i ocenę jako zmienną odpowiedzi:
#import necessary libraries import matplotlib.pyplot as plt import statsmodels.api as sm from statsmodels.formula.api import ols #fit simple linear regression model model = ols('rating ~ points', data=df). fit () #view model summary print(model.summary())
Możemy utworzyć wykres rezydualny lub dopasowany za pomocą funkcji plot_regress_exog() z biblioteki statsmodels:
#define figure size fig = plt.figure(figsize=(12,8)) #produce regression plots fig = sm.graphics.plot_regress_exog(model, ' points ', fig=fig)
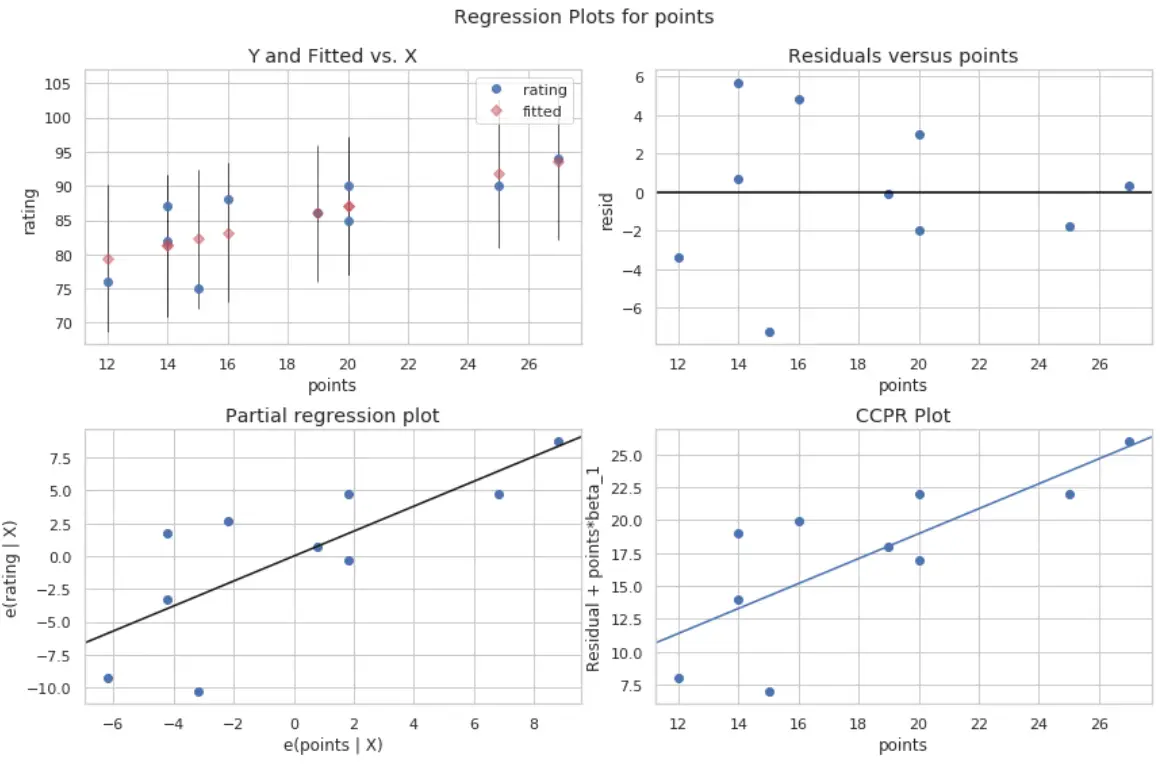
Produkowane są cztery działki. Ten w prawym górnym rogu przedstawia wykres rezydualny w porównaniu z wykresem skorygowanym. Oś x na tym wykresie pokazuje rzeczywiste wartości punktów zmiennych predykcyjnych, a oś y pokazuje resztę dla tej wartości.
Ponieważ reszty wydają się być losowo rozproszone wokół zera, oznacza to, że heteroskedastyczność nie jest problemem w przypadku zmiennej predykcyjnej.
Wykresy reszt dla wielokrotnej regresji liniowej
Załóżmy, że zamiast tego dopasowujemy model regresji liniowej, wykorzystując asysty i zbiórki jako zmienną predykcyjną oraz ocenę jako zmienną odpowiedzi:
#fit multiple linear regression model model = ols('rating ~ assists + rebounds', data=df). fit () #view model summary print(model.summary())
Po raz kolejny możemy utworzyć wykres reszt w funkcji predyktorów dla każdego z poszczególnych predyktorów, korzystając z funkcji plot_regress_exog() z biblioteki statsmodels.
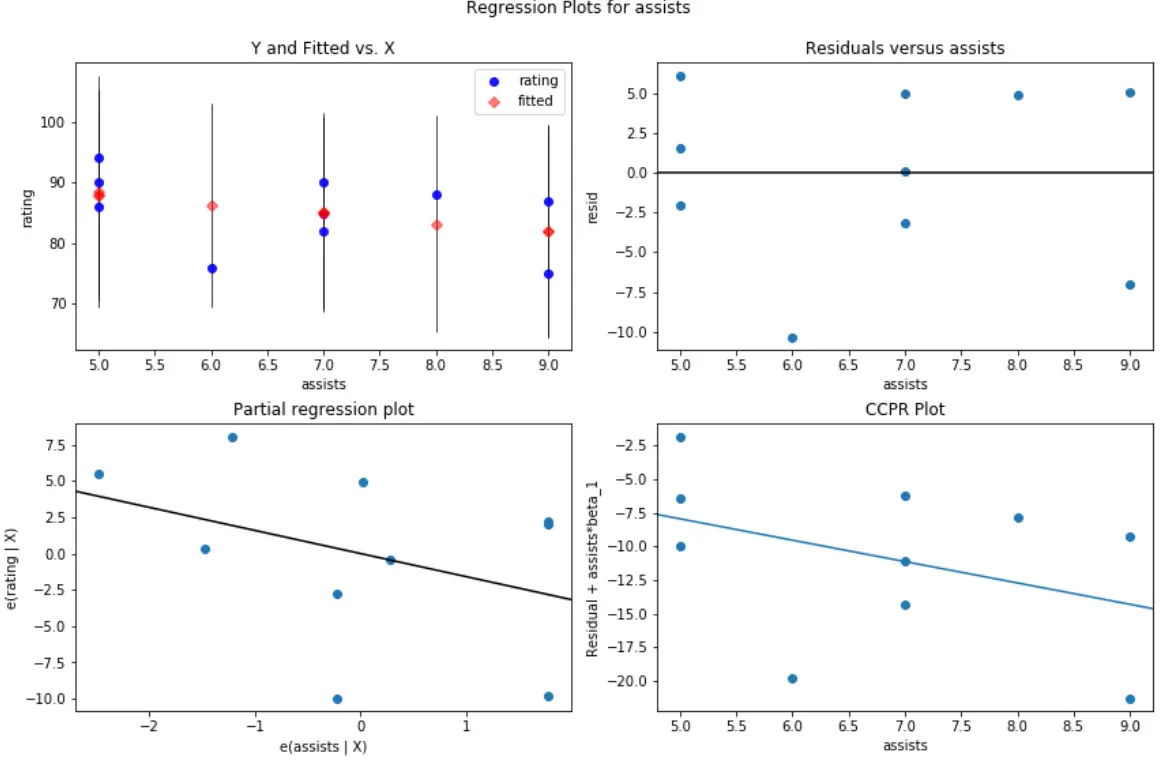
Na przykład tak wygląda wykres reszt/predyktorów dla asystujących zmiennych predykcyjnych :
#create residual vs. predictor plot for 'assists' fig = plt.figure(figsize=(12,8)) fig = sm.graphics.plot_regress_exog(model, ' assists ', fig=fig)
A tak wygląda wykres reszt/predyktorów dla odbić zmiennej predykcyjnej:
#create residual vs. predictor plot for 'assists' fig = plt.figure(figsize=(12,8)) fig = sm.graphics.plot_regress_exog(model, ' rebounds ', fig=fig)
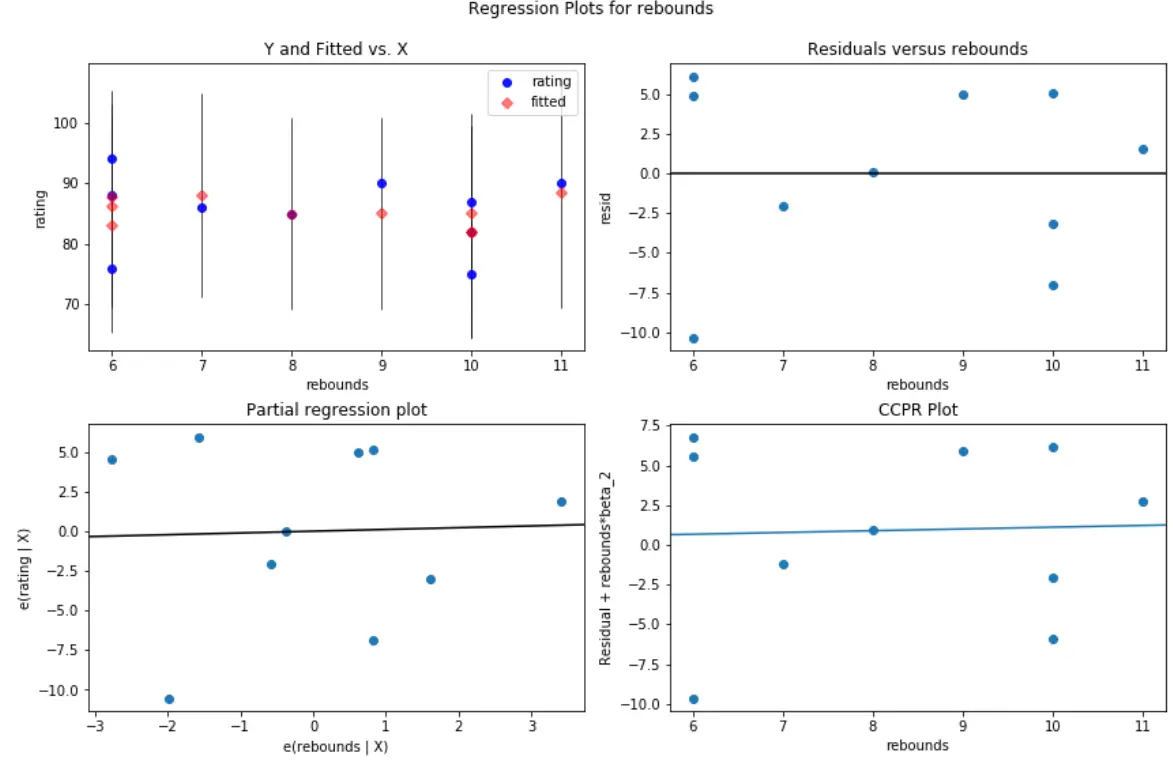
Na obu wykresach reszty wydają się być losowo rozproszone wokół zera, co wskazuje, że heteroskedastyczność nie stanowi problemu w przypadku żadnej ze zmiennych predykcyjnych w modelu.