Prawo wielkich liczb: definicja + przykłady
Prawo wielkich liczb mówi, że wraz ze wzrostem wielkości próby średnia próbki zbliża się do wartości oczekiwanej.
Najbardziej podstawowym przykładem jest rzut monetą. Za każdym razem, gdy rzucamy monetą, prawdopodobieństwo, że wypadnie reszka, wynosi 1/2. Zatem oczekiwana proporcja orłów, które pojawią się w nieskończonej liczbie rzutów, wynosi 1/2 lub 0,5 .
Jeśli jednak rzucimy monetą 10 razy, może się okazać, że wypadnie reszka tylko 3 razy. Ponieważ 10 rzutów to mała próbka, nie ma gwarancji, że proporcja główki będzie bliska 0,5 .
Jeśli będziemy rzucać monetą jeszcze 10 razy, może się okazać, że wypadnie orzeł w sumie 9 razy na 20. Jeśli rzucimy ją jeszcze 10 razy, może się okazać, że wypadnie orzeł 22 na 30.
Gdy rzucimy monetą, odsetek wypadnięć reszek zbiegnie się do oczekiwanej proporcji 0,5 .
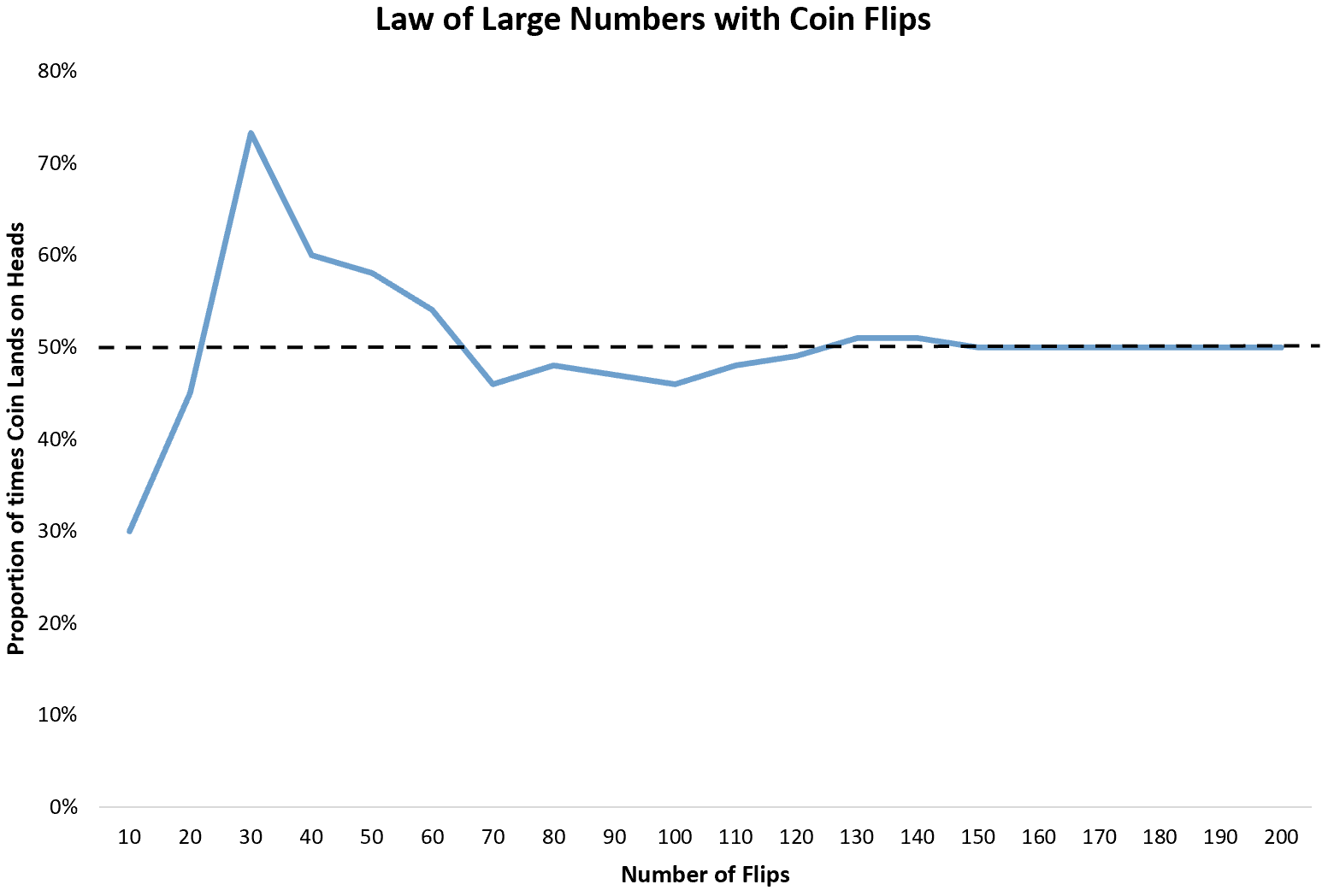
Ta prosta idea prawa wielkich liczb jest stosowana w prawdziwym życiu przez wiele rodzajów firm i branż.
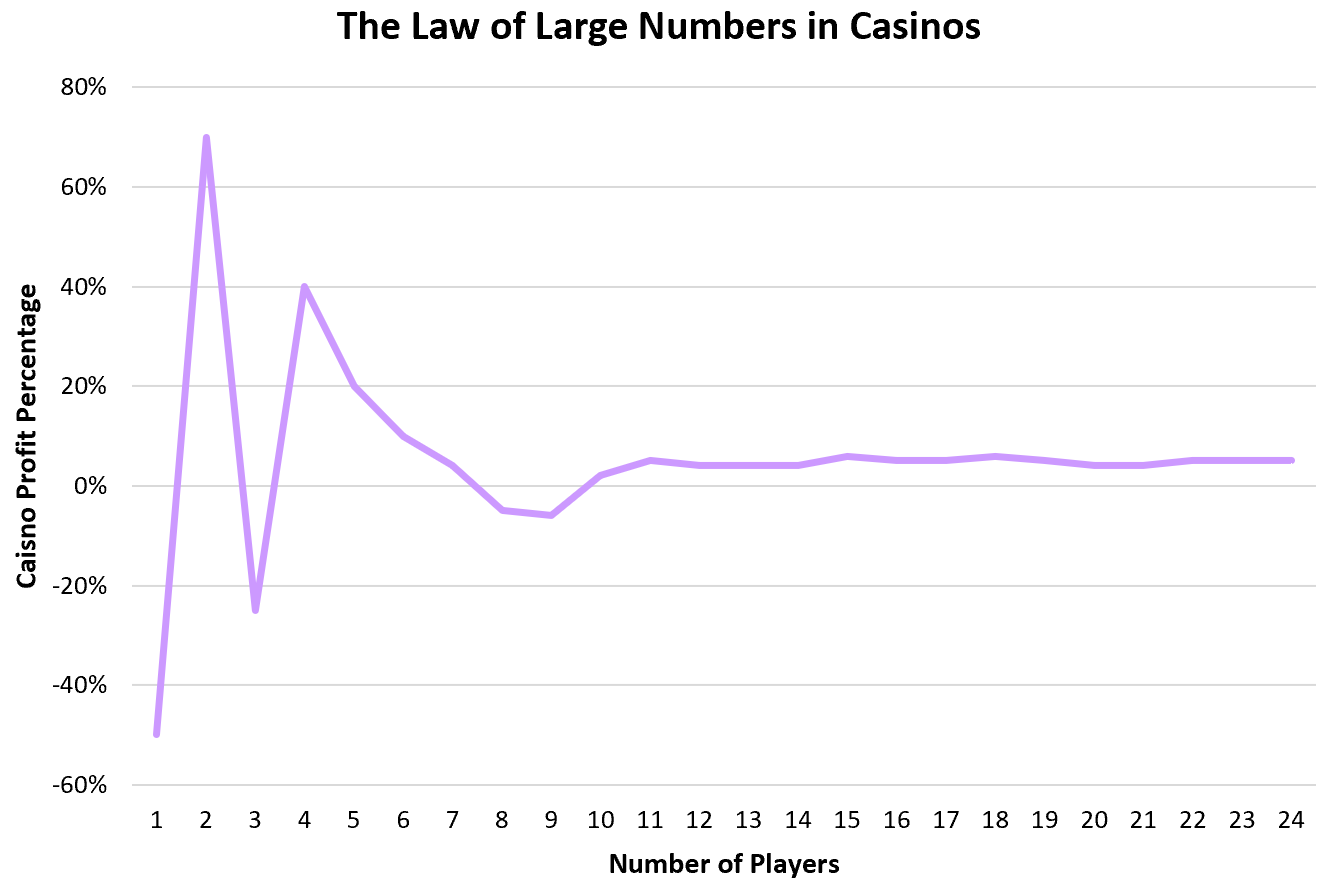
Prawo wielkich liczb w kasynach
Aby niezawodnie generować zyski, kasyna opierają się na prawie wielkich liczb. W przypadku większości gier kasyno wygrywa w około 51-55% przypadków. Oznacza to, że pojedyncze osoby mogą mieć szczęście i od czasu do czasu wygrać przyzwoitą kwotę, ale spośród dziesiątek tysięcy indywidualnych graczy kasyno wygra w oczekiwanych 51-55% przypadków.
Na przykład Jessica może zagrać w kilka gier w kasynie i wygrać 50 dolarów.
Mike mógłby także rozegrać kilka gier i stracić 70 dolarów.
John mógłby rozegrać kilka gier i wygrać 25 dolarów.
Susan mogłaby rozegrać kilka gier i stracić 40 dolarów.
Niektórzy gracze wygrają pieniądze, a inni stracą pieniądze, ale ze względu na sposób, w jaki zaprojektowano gry, kasyna mogą być pewne, że wygrają spośród tysięcy osób.
Prawo wielkich liczb w ubezpieczeniach
Aby zachować rentowność, towarzystwa ubezpieczeniowe również opierają się na prawie wielkich liczb.
Podstawową ideą jest to, że tysiące firm ubezpieczeniowych może zapewnić ubezpieczenie osobom, które płacą co miesiąc określoną składkę, i że tylko niewielki procent ubezpieczonych przez nie osób będzie faktycznie musiał skorzystać z ubezpieczenia, aby pokryć główne, nieoczekiwane wydatki.
Na przykład każdy z 1000 osób mógłby płacić 1000 dolarów rocznie za ubezpieczenie, co wygenerowałoby zysk w wysokości 1 000 000 dolarów dla firmy ubezpieczeniowej.
Jednakże każda z 90 osób może potrzebować otrzymać od firmy ubezpieczeniowej 10 000 dolarów na pokrycie nieoczekiwanych wydatków związanych z różnymi wypadkami, co spowoduje stratę dla firmy ubezpieczeniowej w wysokości 900 000 dolarów.
Ostatecznie firma ubezpieczeniowa osiąga zysk w wysokości 1 000 000 USD – 900 000 USD = 100 000 USD .
Oznacza to, że firma ubezpieczeniowa może spodziewać się dość przewidywalnego zysku średnio na tysiącach osób.
Należy pamiętać, że ten model ekonomiczny działa, ponieważ firma ubezpieczeniowa ubezpiecza dużą liczbę osób . Gdyby ubezpieczyli tylko 10 osób, byłoby to zbyt ryzykowne, ponieważ duży, nieoczekiwany wydatek mógłby zniszczyć firmę.
Dlatego firmy ubezpieczeniowe opierają się na prawie wielkich liczb, aby prognozować swoje zyski w przewidywalny sposób.
Prawo wielkich liczb w energii odnawialnej
Z prawa wielkich liczb korzystają także przedsiębiorstwa zajmujące się energią odnawialną.
Podstawową ideą jest to, że turbiny wiatrowe i panele słoneczne mogą zasilać generatory w celu wytwarzania energii elektrycznej w różnych częściach przedsiębiorstwa. Jednak na zewnątrz nie ma wiatru ani słońca, co oznacza, że turbiny wiatrowe i panele słoneczne nie zawsze są w stanie wytworzyć niezawodną energię dla generatorów elektrycznych.
Sposobem, w jaki przedsiębiorstwa zajmujące się energią odnawialną obchodzą ten problem, jest podłączenie dziesiątek tysięcy turbin wiatrowych lub paneli słonecznych do jednej sieci energetycznej, co znacznie zwiększa prawdopodobieństwo, że te źródła energii będą wytwarzać niezawodną ilość energii. energię dla sieci.
Dużo łatwiej jest też przewidzieć, ile energii wyprodukują te źródła energii, ponieważ inżynierowie mogą po prostu przyjąć oczekiwaną średnią z dziesiątek tysięcy turbin wiatrowych lub paneli słonecznych.
Szczegółowe wyjaśnienie tego zjawiska można znaleźć w artykule w czasopiśmie Scientific American .