Operacje na zbiorach: suma, przecięcie, uzupełnienie i różnica
Zbiór to zbiór elementów.
Zbiór oznaczamy dużą literą, a elementy zbioru definiujemy za pomocą nawiasów klamrowych. Załóżmy na przykład, że mamy zbiór o nazwie „A” z elementami 1, 2, 3. Zapisalibyśmy to w następujący sposób:
ZA = {1, 2, 3}
W tym samouczku wyjaśniono najczęściej używane operacje na zbiorach w prawdopodobieństwie i statystyce.
unia
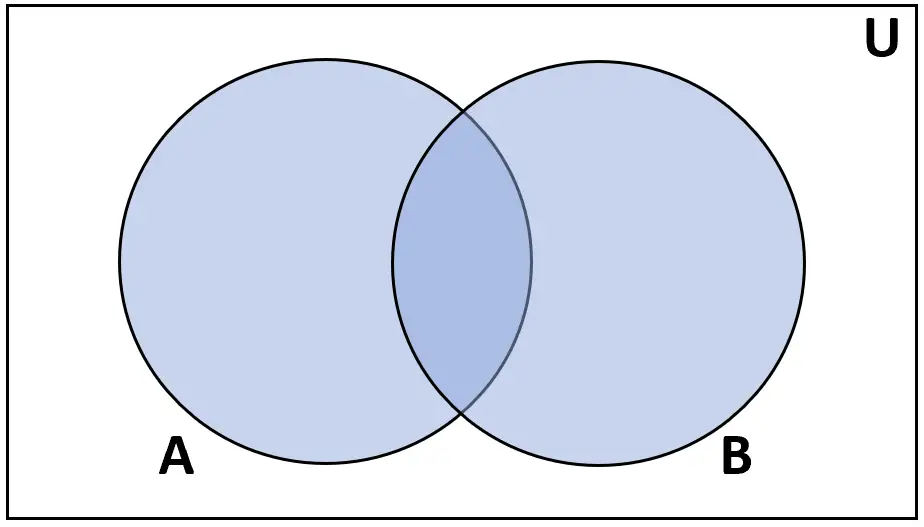
Definicja: Suma zbiorów A i B to zbiór elementów występujących w A lub B.
Ocena: A ∪ B
Przykłady:
- {1, 2, 3} ∪ {4, 5, 6} = {1, 2, 3, 4, 5, 6}
- {1, 2} ∪ {1, 2} = {1, 2}
- {1, 2, 3} ∪ {3, 4} = {1, 2, 3, 4}
Skrzyżowanie
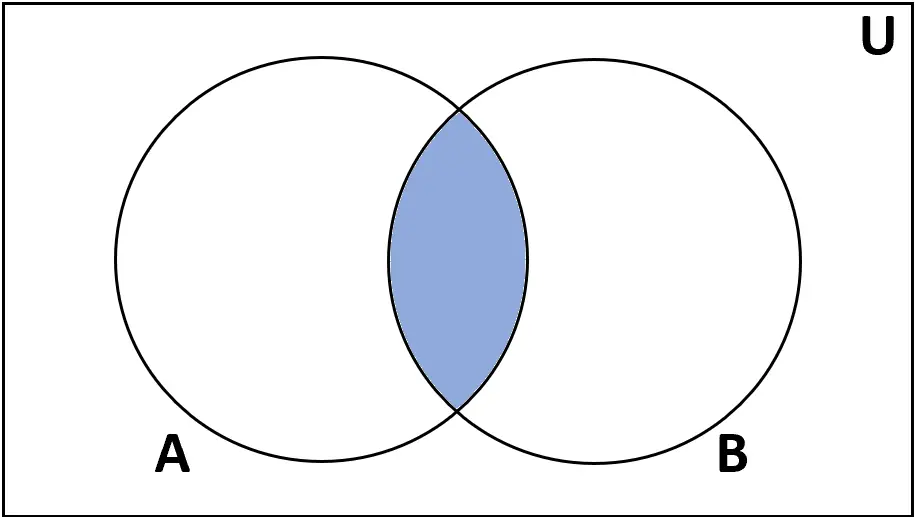
Definicja: Przecięciem zbiorów A i B jest zbiór elementów, które znajdują się zarówno w A, jak i B.
Notacja: A ∩ B
Przykłady:
- {1, 2, 3} ∩ {4, 5, 6} = {∅}
- {1, 2} ∩ {1, 2} = {1, 2}
- {1, 2, 3} ∩ {3, 4} = {3}
Komplement
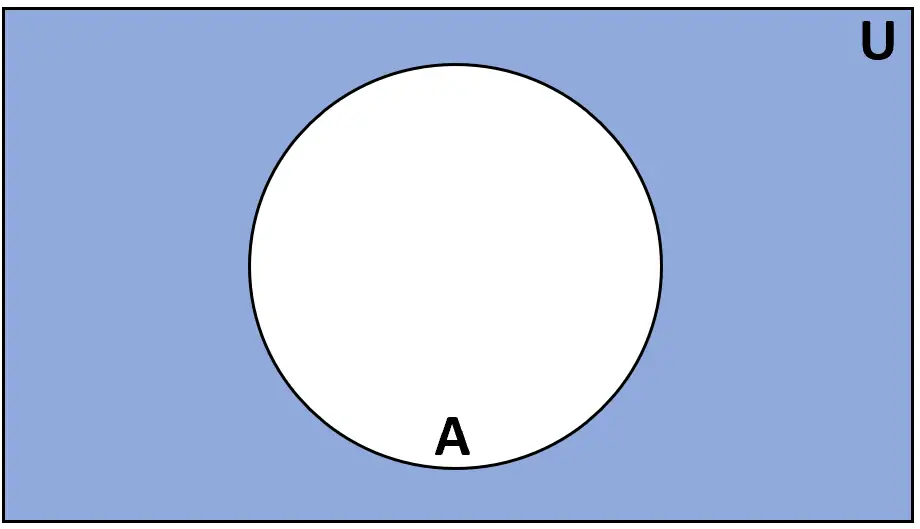
Definicja: Dopełnieniem zbioru A jest zbiór elementów, które znajdują się w zbiorze uniwersalnym U, ale nie należą do A.
Ocena: A’ lub Ac
Przykłady:
- Jeśli U = {1, 2, 3, 4, 5, 6} i A = {1, 2}, to A c = {3, 4, 5, 6}
- Jeśli U = {1, 2, 3} i A = {1, 2}, to A c = {3}
Różnica
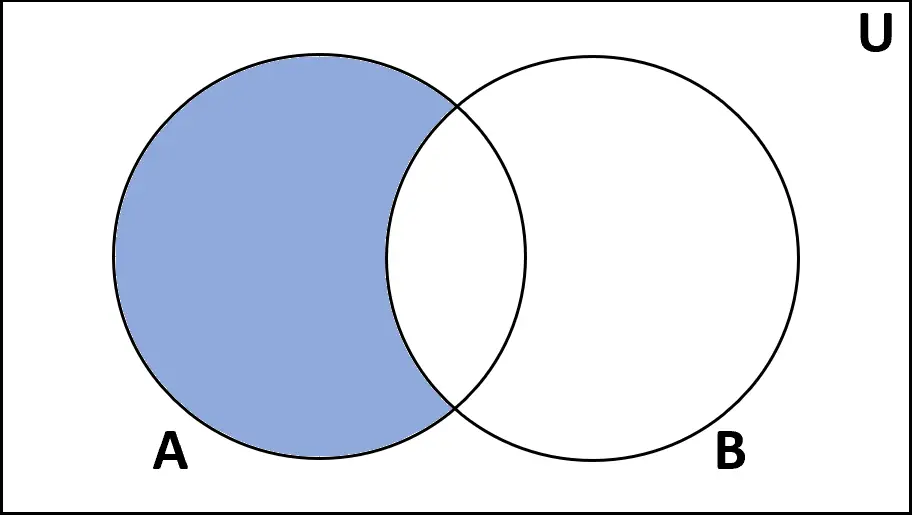
Definicja: Różnica między zbiorami A i B to zbiór elementów, które znajdują się w A, ale nie w B.
Oceny: A–B
Przykłady:
- {1, 2, 3} – {2, 3, 4} = {1}
- {1, 2} – {1, 2} = {∅}
- {1, 2, 3} – {4, 5} = {1, 2, 3}
Różnica symetryczna
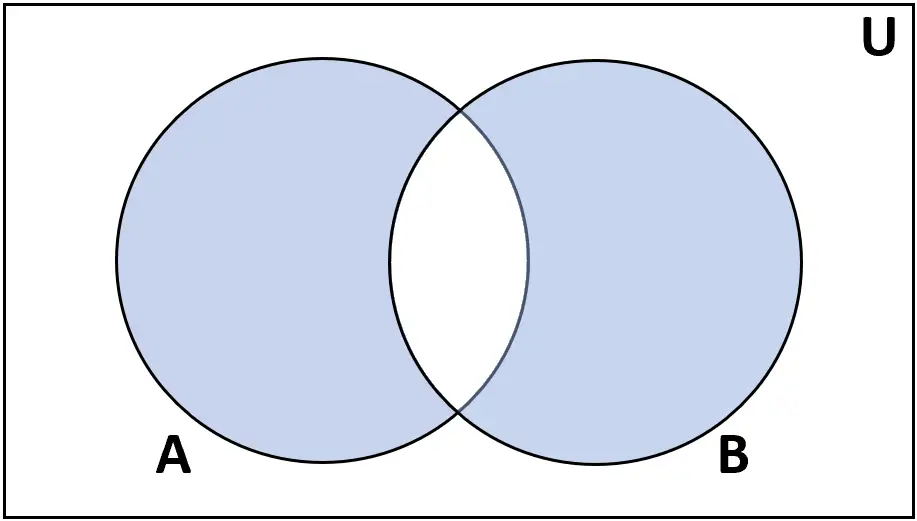
Definicja: Symetryczna różnica zbiorów A i B to zbiór elementów występujących w A lub B, ale nie w obu.
Ocena: AΔB
Przykłady:
- {1, 2, 3} Δ {2, 3, 4} = {1, 4}
- {1, 2} Δ {1, 2} = {∅}
- {1, 2, 3} Δ {4, 5} = {1, 2, 3, 4, 5}
Produkt kartezjański
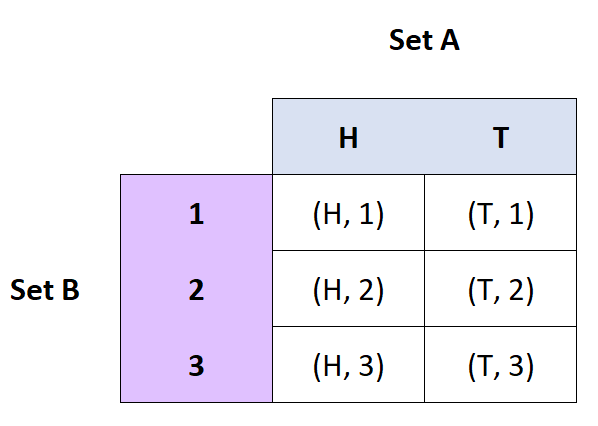
Definicja: Iloczyn kartezjański zbiorów A i B jest zbiorem uporządkowanych par zbiorów A i B.
Ocena: A x B
Przykłady:
- Jeśli A = {H, T} i B = {1, 2, 3}, to A x B = {(H, 1), (H, 2), (H, 3), (T, 1), ( T, 2), (T, 3)}
- Jeśli A = {T, H} i B = {1, 2, 3}, to A x B = {(T, 1), (T, 2), (T, 3), (H, 1), ( H, 2), (H, 3)}