Jak przeprowadzić analizę dwuwymiarową w r (z przykładami)

Termin analiza dwuwymiarowa odnosi się do analizy dwóch zmiennych. Możesz to zapamiętać, ponieważ przedrostek „bi” oznacza „dwa”.

Celem analizy dwuwymiarowej jest zrozumienie związku między dwiema zmiennymi

Istnieją trzy popularne sposoby przeprowadzania analizy dwuwymiarowej:

1. Chmury punktów

2. Współczynniki korelacji

3. Prosta regresja liniowa

Poniższy przykład ilustruje, jak przeprowadzić każdy z tych typów analizy dwuwymiarowej przy użyciu następującego zestawu danych, który zawiera informacje o dwóch zmiennych: (1) godziny spędzone na nauce i (2) wyniki testów uzyskane przez 20 różnych uczniów:

 #create data frame
df <- data. frame (hours=c(1, 1, 1, 2, 2, 2, 3, 3, 3, 3,
                         3, 4, 4, 5, 5, 6, 6, 6, 7, 8),
                 score=c(75, 66, 68, 74, 78, 72, 85, 82, 90, 82,
                         80, 88, 85, 90, 92, 94, 94, 88, 91, 96))

#view first six rows of data frame
head(df)

  hours score
1 1 75
2 1 66
3 1 68
4 2 74
5 2 78
6 2 72

1. Chmury punktów

Możemy użyć następującej składni, aby utworzyć wykres rozrzutu godzin przestudiowanych w funkcji ocen z egzaminu w R:

 #create scatterplot of hours studied vs. exam score
plot(df$hours, df$score, pch= 16 , col=' steelblue ',
     main=' Hours Studied vs. Exam Score ',
     xlab=' Hours Studied ', ylab=' Exam Score ')

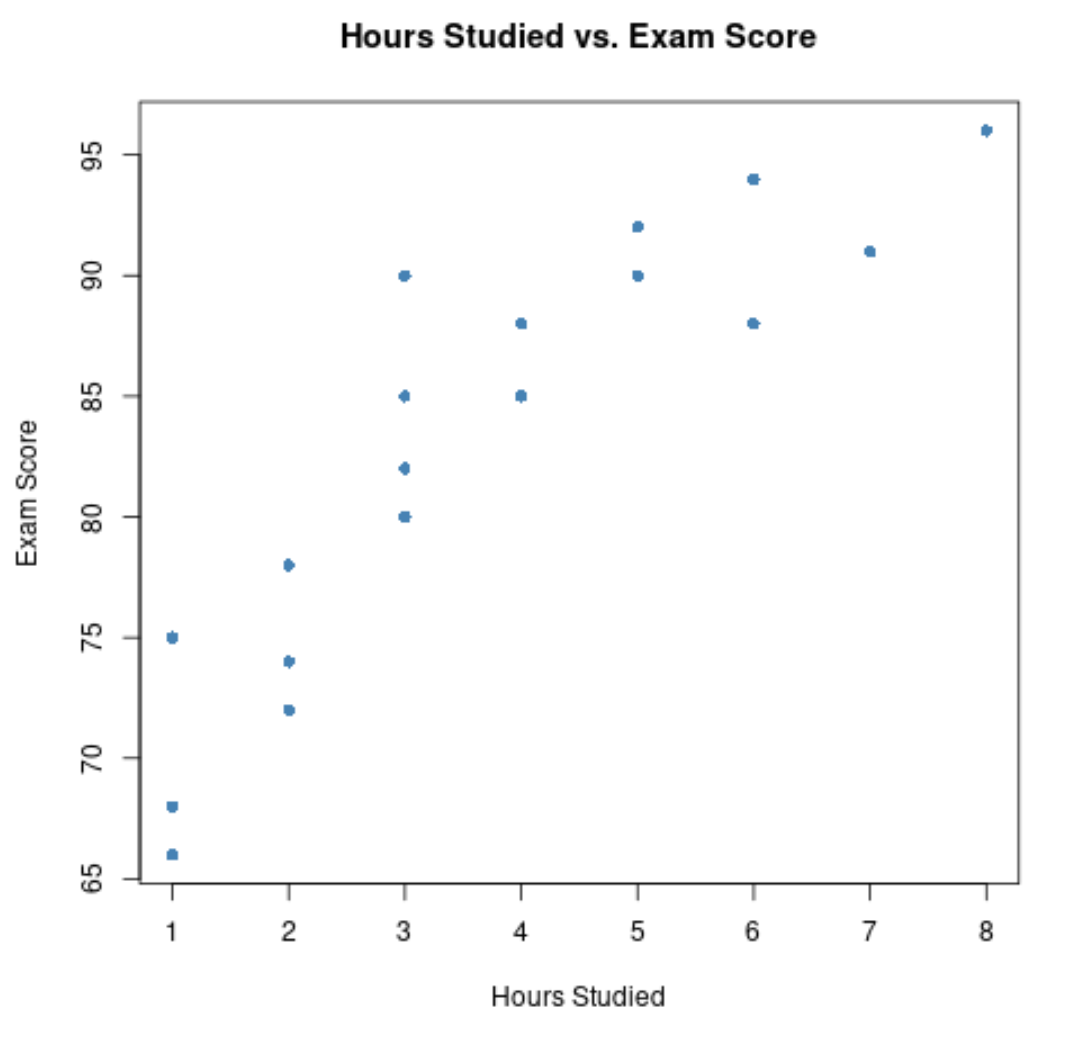
Oś x pokazuje liczbę przepracowanych godzin, a oś y ocenę uzyskaną na egzaminie.

Wykres pokazuje, że istnieje pozytywna zależność między tymi dwiema zmiennymi: wraz ze wzrostem liczby godzin nauki zwiększają się również wyniki egzaminów.

2. Współczynniki korelacji

Współczynnik korelacji Pearsona to sposób na ilościowe określenie liniowej zależności między dwiema zmiennymi.

Możemy użyć funkcji cor() w R, aby obliczyć współczynnik korelacji Pearsona między dwiema zmiennymi:

 #calculate correlation between hours studied and exam score received
cor(df$hours, df$score)

[1] 0.891306

Współczynnik korelacji okazuje się wynosić 0,891 .

Wartość ta jest bliska 1, co wskazuje na silną dodatnią korelację pomiędzy przestudiowanymi godzinami a oceną z egzaminu.

3. Prosta regresja liniowa

Prosta regresja liniowa to metoda statystyczna, której możemy użyć do znalezienia równania prostej, która najlepiej „pasuje” do zbioru danych, a które możemy następnie wykorzystać do zrozumienia dokładnej zależności między dwiema zmiennymi.

Możemy użyć funkcji lm() w R, aby dopasować prosty model regresji liniowej dla przestudiowanych godzin i otrzymanych wyników egzaminów:

 #fit simple linear regression model
fit <- lm(score ~ hours, data=df)

#view summary of model
summary(fit)

Call:
lm(formula = score ~ hours, data = df)

Residuals:
   Min 1Q Median 3Q Max 
-6,920 -3,927 1,309 1,903 9,385 

Coefficients:
            Estimate Std. Error t value Pr(>|t|)    
(Intercept) 69.0734 1.9651 35.15 < 2nd-16 ***
hours 3.8471 0.4613 8.34 1.35e-07 ***
---
Significant. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 4.171 on 18 degrees of freedom
Multiple R-squared: 0.7944, Adjusted R-squared: 0.783 
F-statistic: 69.56 on 1 and 18 DF, p-value: 1.347e-07

Dopasowane równanie regresji okazuje się mieć postać:

Wynik egzaminu = 69,0734 + 3,8471*(godziny nauki)

To mówi nam, że każda dodatkowa godzina nauki wiąże się ze średnim wzrostem wyniku egzaminu o 3,8471 .

Możemy również użyć dopasowanego równania regresji, aby przewidzieć wynik, jaki otrzyma uczeń na podstawie całkowitej liczby przestudiowanych godzin.

Przykładowo student studiujący 3 godziny powinien uzyskać wynik 81,6147 :

• Wynik egzaminu = 69,0734 + 3,8471*(godziny nauki)
• Wynik egzaminu = 69,0734 + 3,8471*(3)
• Wynik egzaminu = 81,6147

Dodatkowe zasoby

Poniższe samouczki zawierają dodatkowe informacje na temat analizy dwuwymiarowej:

Wprowadzenie do analizy dwuwymiarowej
5 przykładów danych dwuwymiarowych w prawdziwym życiu
Wprowadzenie do prostej regresji liniowej