Jak przeprowadzić analizę głównych komponentów w sas-ie

Analiza głównych składowych (PCA) to technika uczenia maszynowego bez nadzoru , która ma na celu znalezienie głównych składowych – liniowych kombinacji zmiennych predykcyjnych – wyjaśniających dużą część zmienności w zbiorze danych.

Najprostszym sposobem wykonania PCA w SAS-ie jest użycie instrukcji PROC PRINCOMP , która wykorzystuje następującą podstawową składnię:

 proc princomp data =my_data out =out_data outstat =stats;
    var var1 var2 var3;
run ;

Oto, co robi każda instrukcja:

• dane : nazwa zbioru danych, który będzie używany dla PCA
• out : nazwa zestawu danych do utworzenia, który zawiera wszystkie oryginalne dane oraz wyniki głównych składników
• outstat : Określa, że należy utworzyć zbiór danych zawierający średnie, odchylenia standardowe, współczynniki korelacji, wartości własne i wektory własne.
• var : zmienne, które mają być użyte dla PCA z wejściowego zbioru danych.

Poniższy przykład pokazuje krok po kroku, jak w praktyce wykorzystać instrukcję PROC PRINCOMP do przeprowadzenia analizy głównych składowych w SAS-ie.

Krok 1: Utwórz zbiór danych

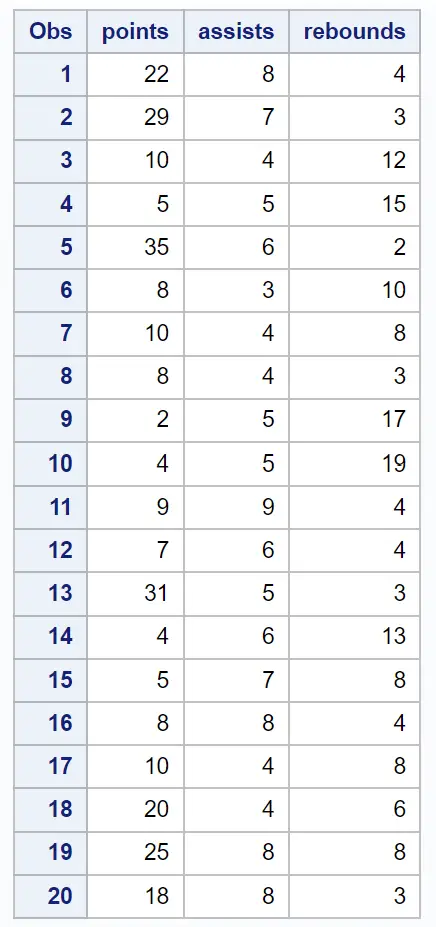
Załóżmy, że mamy następujący zbiór danych zawierający różne informacje na temat 20 koszykarzy:

 /*create dataset*/
data my_data;
    input points assists rebounds;
    datalines ;
22 8 4
29 7 3
10 4 12
5 5 15
35 6 2
8 3 10
10 4 8
8 4 3
2 5 17
4 5 19
9 9 4
7 6 4
31 5 3
4 6 13
5 7 8
8 8 4
10 4 8
20 4 6
25 8 8
18 8 3
;
run ;

/*view dataset*/
proc print data =my_data; 

Krok 2: Wykonaj analizę głównych składowych

Możemy użyć instrukcji PROC PRINCOMP , aby przeprowadzić analizę głównych składowych przy użyciu zmiennych punktów , asyst i odbić ze zbioru danych:

 /*perform principal components analysis*/
proc princomp data =my_data out =out_data outstat =stats;
    var points assists rebounds;
run ;

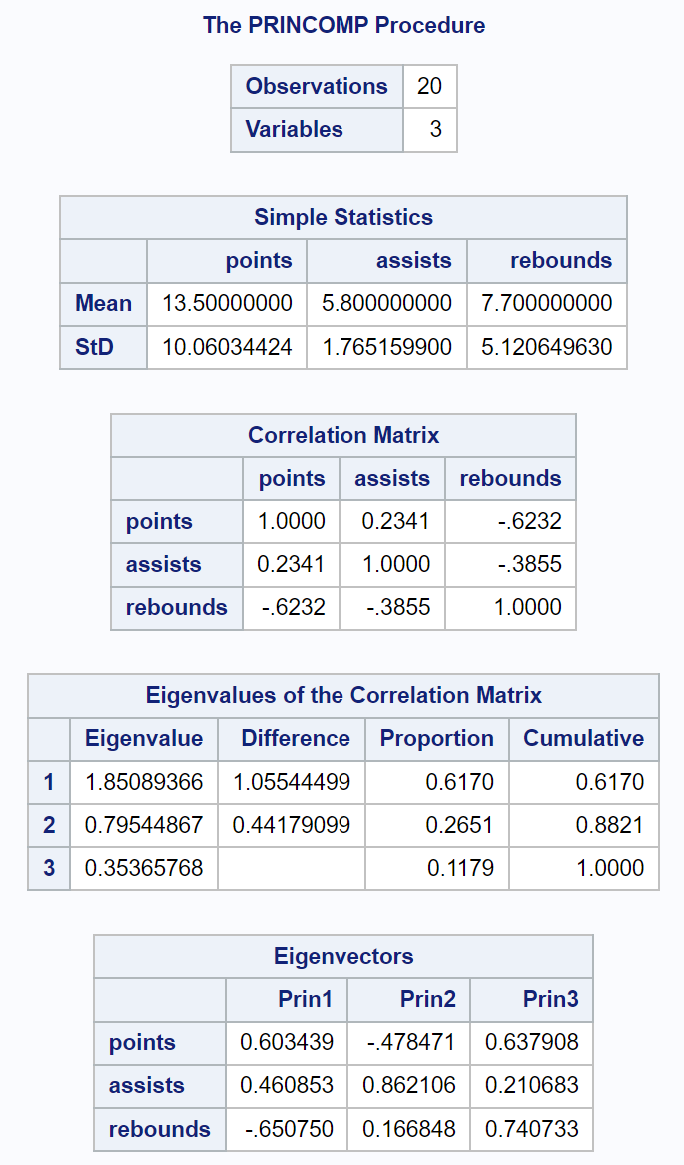
Pierwsza część wyników wyświetla różne statystyki opisowe, w tym średnie i odchylenia standardowe każdej zmiennej wejściowej, macierz korelacji oraz wartości wartości własnych i wektorów własnych:

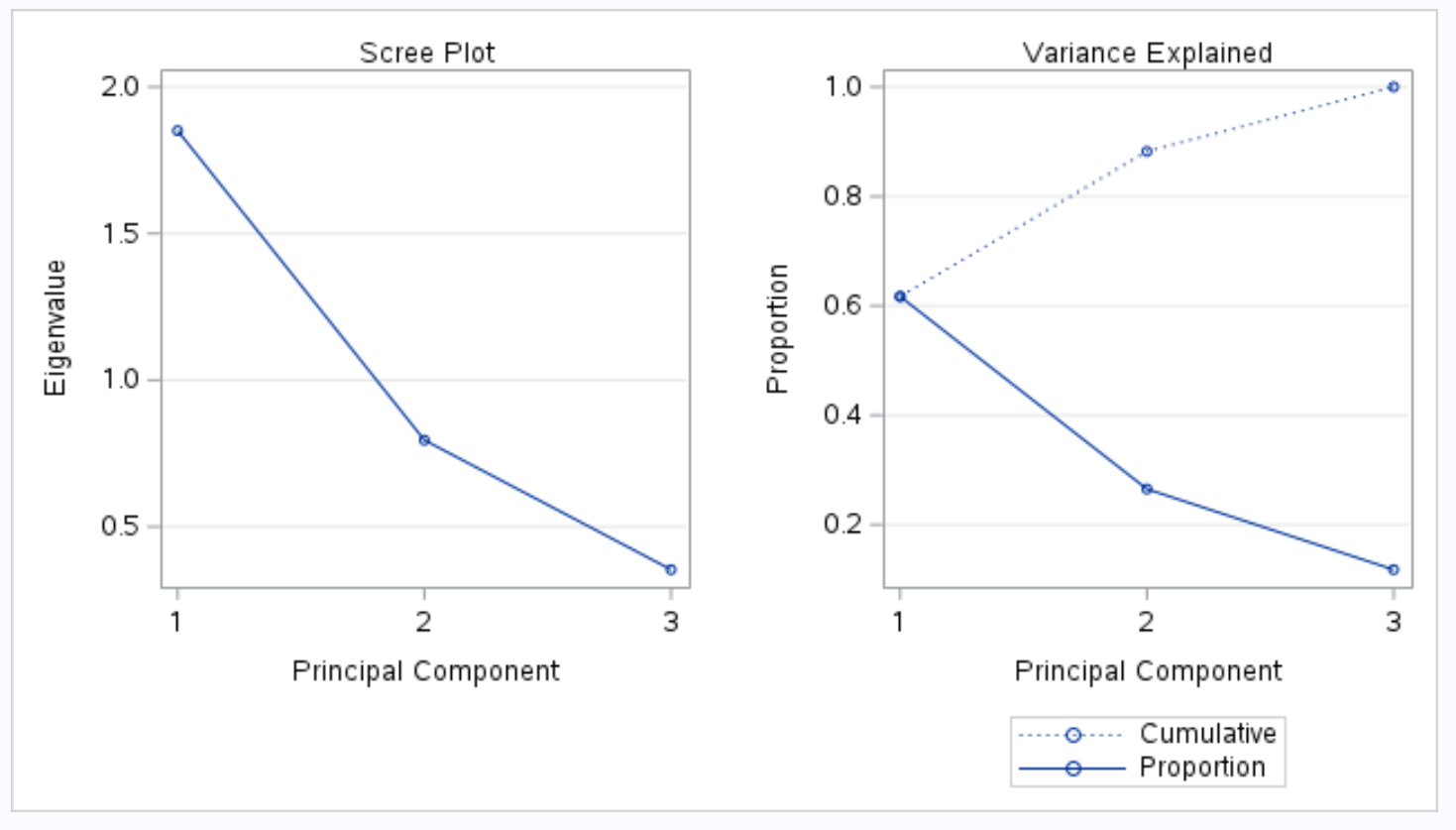
Następna część wyników wyświetla wykres osypiska i wyjaśniony wykres wariancji :

Kiedy przeprowadzamy PCA, często chcemy zrozumieć, jaki procent całkowitej zmienności w zbiorze danych można wyjaśnić każdym głównym składnikiem.

Wynikowa tabela zatytułowana Wartości własne macierzy korelacji pozwala nam dokładnie zobaczyć, jaki procent całkowitej zmienności jest wyjaśniony przez każdy główny składnik:

• Pierwszy główny składnik wyjaśnia 61,7% całkowitej zmienności zbioru danych.
• Drugi główny składnik wyjaśnia 26,51% całkowitej zmienności zbioru danych.
• Trzeci główny składnik wyjaśnia 11,79% całkowitej zmienności zbioru danych.

Należy pamiętać, że wszystkie wartości procentowe sumują się do 100%.

Wykres zatytułowany Wyjaśnienie wariancji pozwala nam następnie zwizualizować te wartości.

Oś x przedstawia główny składnik, a oś y przedstawia procent całkowitej wariancji wyjaśnionej przez każdy pojedynczy główny składnik.

Krok 3: Utwórz biplot, aby zwizualizować wyniki

Aby zwizualizować wyniki PCA dla danego zbioru danych, możemy utworzyć biplot , czyli wykres przedstawiający każdą obserwację w zbiorze danych na płaszczyźnie utworzonej przez pierwsze dwa główne składniki.

Do utworzenia biplotu możemy użyć następującej składni w SAS-ie:

 /*create dataset with column called obs to represent row numbers of original data*/
data biplot_data;
   set out_data;
   obs=_n_;
run ;

/*create biplot using values from first two principal components*/
proc sgplot data =biplot_data;
    scatter x =Prin1 y =Prin2 / datalabel =obs;
run ; 

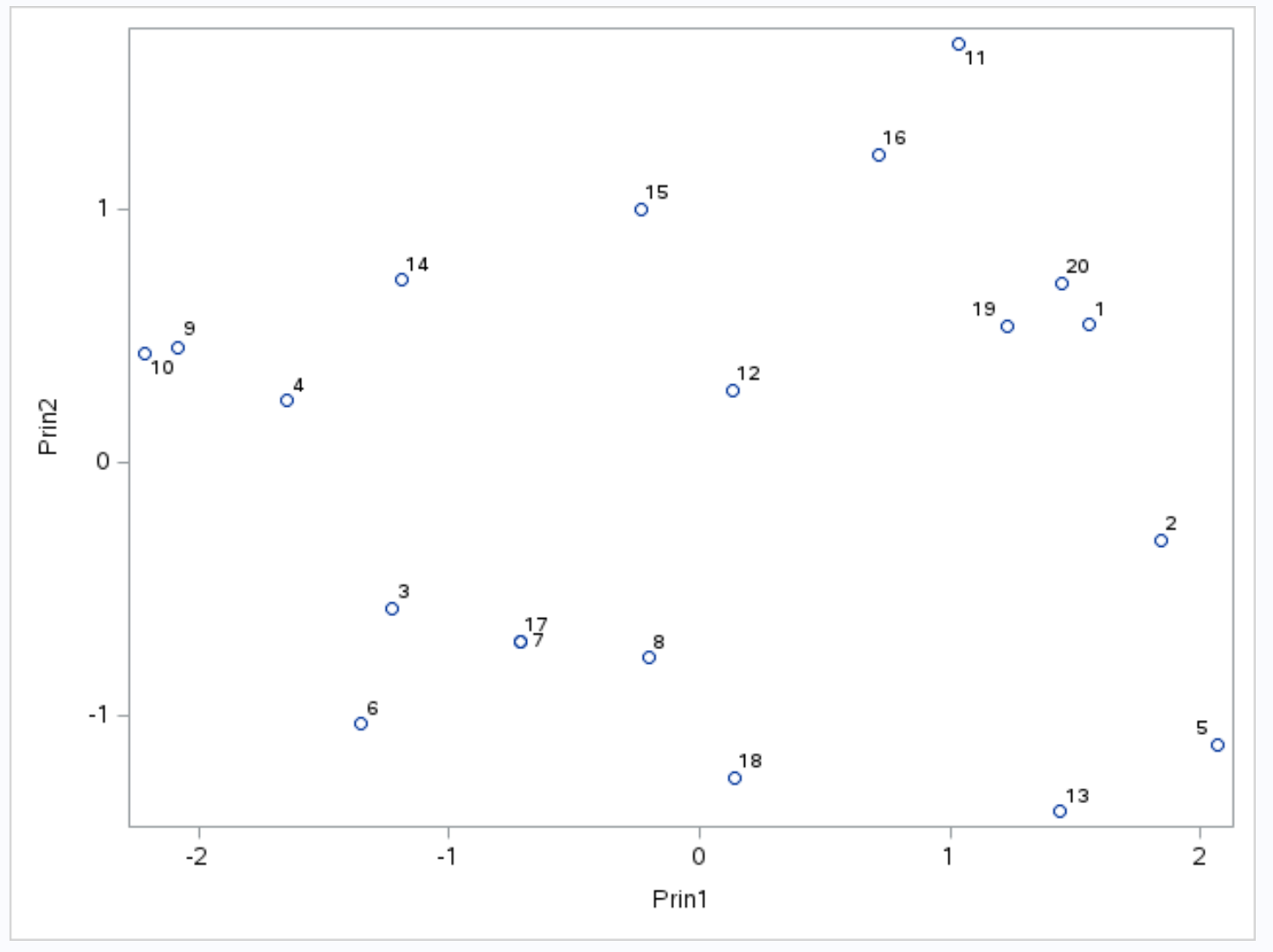
Oś x przedstawia pierwszy główny składnik, oś y przedstawia drugi główny składnik, a poszczególne obserwacje ze zbioru danych są wyświetlane na wykresie w postaci małych okręgów.

Obserwacje umieszczone obok siebie na wykresie mają podobne wartości dla trzech zmiennych: punktów , asyst i zbiórek .

Na przykład po lewej stronie wykresu widać, że obserwacje nr 9 i 10 są bardzo blisko siebie.

Jeśli odniesiemy się do oryginalnego zbioru danych, możemy zobaczyć następujące wartości dla tych obserwacji:

• Obserwacja nr 9 : 2 punkty, 5 asyst, 17 zbiórek
• Obserwacja nr 10 : 4 punkty, 5 asyst, 19 zbiórek

Wartości są podobne dla każdej z trzech zmiennych, co wyjaśnia, dlaczego te obserwacje są tak blisko siebie na biplocie.

W tabeli wyników zatytułowanej Wartości własne macierzy korelacji widzieliśmy również, że pierwsze dwa główne składniki stanowią 88,21% całkowitej zmienności zbioru danych.

Ponieważ odsetek ten jest bardzo wysoki, zasadne jest przeanalizowanie, które obserwacje w biplot są blisko siebie, ponieważ dwa główne elementy tworzące biplot odpowiadają za prawie całą zmienność zbioru danych.

Dodatkowe zasoby

Poniższe samouczki wyjaśniają, jak wykonywać inne typowe zadania w SAS-ie:

Jak wykonać prostą regresję liniową w SAS-ie
Jak wykonać wielokrotną regresję liniową w SAS-ie
Jak przeprowadzić regresję logistyczną w SAS-ie