Wprowadzenie do ancova (analiza wariancji)

ANCOVA oznacza „analizę kowariancji”. Aby zrozumieć, jak działa ANCOVA, warto najpierw zrozumieć ANOVA.

ANOVA _   (analiza wariancji) służy do ustalenia, czy istnieje statystycznie istotna różnica między średnimi trzech lub więcej niezależnych grup.

Załóżmy na przykład, że chcemy wiedzieć, czy technika uczenia się wpływa na wyniki egzaminów danej klasy uczniów. Podzieliliśmy klasę losowo na trzy grupy. Każda grupa stosuje inną technikę nauki przez miesiąc, aby przygotować się do egzaminu. Pod koniec miesiąca wszyscy uczniowie przystępują do tego samego egzaminu.

Aby dowiedzieć się, czy technika uczenia się ma wpływ na wyniki egzaminu, możemy przeprowadzić jednoczynnikową analizę ANOVA, która powie nam, czy istnieje statystycznie istotna różnica między średnimi wynikami trzech grup.

ANCOVA jest rozszerzeniem ANOVA, w którym chcemy określić, czy istnieje statystycznie istotna różnica między trzema lub większą liczbą niezależnych grup po uwzględnieniu jednej lub większej liczby współzmiennych .

Współzmienna to zmienna ciągła, która zmienia się wraz ze zmienną odpowiedzi.

Załóżmy na przykład, że chcemy wiedzieć, czy technika uczenia się ma wpływ na wyniki egzaminu, ale chcemy wziąć pod uwagę ocenę, jaką uczeń ma już na zajęciach . Możemy użyć ich aktualnej oceny jako współzmiennej i wykonać ANCOVA, aby określić, czy istnieje statystycznie istotna różnica między średnimi wynikami egzaminów w trzech grupach.

Dzięki temu możemy sprawdzić, czy technika uczenia się ma wpływ na wyniki egzaminu, po usunięciu wpływu współzmiennej.

Jeśli więc stwierdzimy, że istnieje statystycznie istotna różnica w wynikach egzaminów pomiędzy trzema technikami uczenia się, możemy być pewni, że różnica ta istnieje nawet po uwzględnieniu aktualnej oceny uczniów w klasie (c „to znaczy, jeśli już sobie radzą dobrze lub jeśli już dobrze sobie radzą). nie na zajęciach) .

Założenia ANCOVA

Przed wykonaniem ANCOVA ważne jest, aby upewnić się, że spełnione są następujące założenia:

• Współzmienna(e) i zmienna(e) czynnikowa są niezależne – Współzmienna i zmienna czynnikowa muszą być od siebie niezależne, ponieważ dodanie składnika współzmiennej w modelu ma sens tylko wtedy, gdy współzmienna i zmienna czynnikowa działają niezależnie na zmienna odpowiedzi.
• Współzmienna(e) są danymi ciągłymi. Współzmienne muszą być ciągłe (tj. dane interwałowe lub ilorazowe).
• Homogeniczność wariancji – wariancje pomiędzy grupami powinny być w przybliżeniu równe.
• Niezależność – obserwacje w każdej grupie muszą być niezależne.
• Normalność – dane powinny mieć w przybliżeniu rozkład normalny w każdej grupie.
• Brak skrajnych wartości odstających – w żadnej z grup nie powinny występować skrajne wartości odstające, które mogłyby znacząco wpłynąć na wyniki ANCOVA.

ANCOVA: przykład

Nauczycielka chce wiedzieć, czy trzy różne techniki uczenia się wpływają na wyniki egzaminu, ale chce wziąć pod uwagę aktualną ocenę, jaką uczeń ma już w klasie.

Wykona ANCOVA przy użyciu następujących zmiennych:

• Zmienna czynnikowa: badanie techniczne
• Współzmienna: aktualny wynik
• Zmienna odpowiedzi: wynik egzaminu

Poniższa tabela przedstawia zbiór danych 15 studentów zakwalifikowanych do udziału w badaniu:

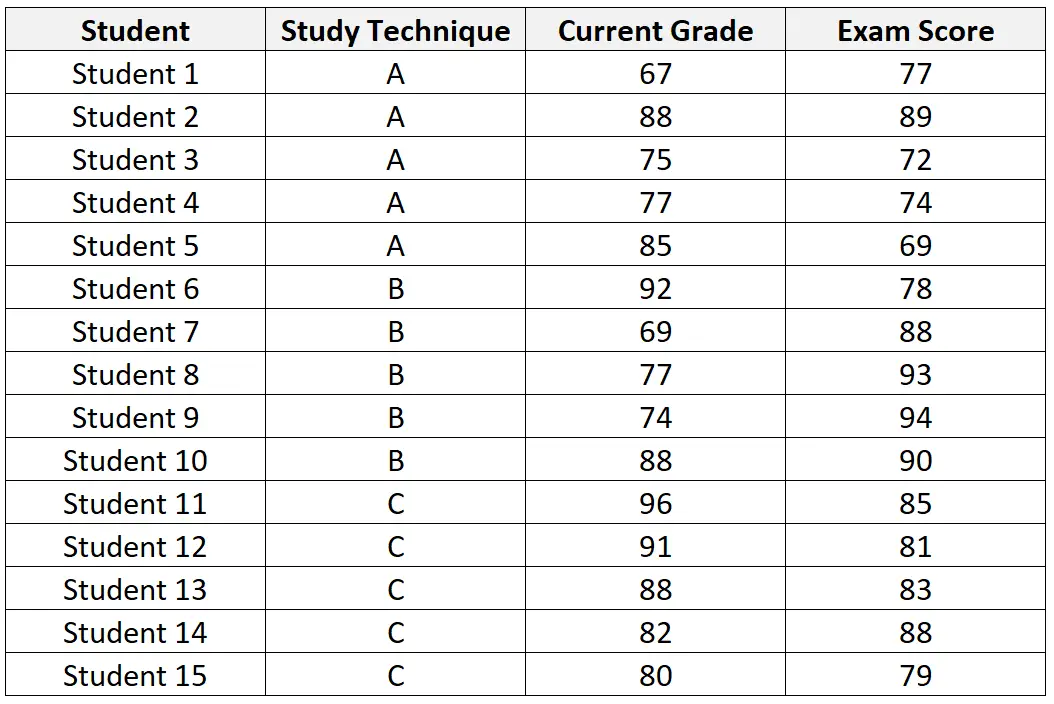
Po wykonaniu ANCOVA na zbiorze danych nauczyciel otrzymuje następujące wyniki:

Wartość p dla techniki badawczej wynosi 0,03155 . Ponieważ wartość ta jest mniejsza niż 0,05, możemy odrzucić hipotezę zerową, że każda z technik badania prowadzi do tej samej średniej oceny z egzaminu, nawet po uwzględnieniu aktualnej oceny studenta z zajęć .

Aby dokładnie określić, które techniki uczenia się dają różne średnie wyniki egzaminu, nauczyciel będzie musiał przeprowadzićtesty post-hoc .

Dodatkowe zasoby

Jak wykonać ANCOVA w programie Excel
Jak wykonać ANCOVA w R
Jak wykonać ANCOVA w Pythonie
Różnice między ANOVA, ANCOVA, MANOVA i MANCOVA