Jak ręcznie wykonać anova z powtarzanymi pomiarami
ANOVA z powtarzanymi pomiarami służy do określenia, czy istnieje statystycznie istotna różnica pomiędzy średnimi z trzech lub więcej grup, w których w każdej grupie pojawiają się ci sami pacjenci.
W tym samouczku wyjaśniono, jak ręcznie wykonać jednokierunkową analizę ANOVA z powtarzanymi pomiarami.
Przykład: Jednokierunkowe powtarzane pomiary ANOVA ręcznie
Naukowcy chcą wiedzieć, czy trzy różne leki powodują różne czasy reakcji. Aby to sprawdzić, mierzą czas reakcji (w sekundach) pięciu pacjentów na każdy lek. Wyniki przedstawiono poniżej:
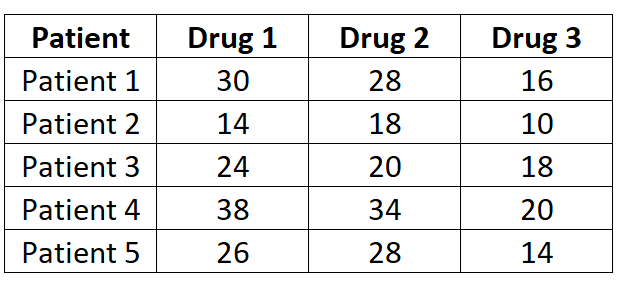
Ponieważ u każdego pacjenta badany jest każdy z trzech leków, użyjemy jednokierunkowej analizy ANOVA z powtarzanymi pomiarami, aby określić, czy średni czas reakcji różni się w zależności od leku.
Aby ręcznie wykonać powtarzane pomiary ANOVA, wykonaj następujące kroki:
Krok 1: Oblicz SST.
Najpierw obliczymy całkowitą sumę kwadratów (SST), którą można obliczyć za pomocą następującego wzoru:
SST = s 2 łącznie (n łącznie -1)
Złoto:
- s 2 suma : wariancja zbioru danych
- n total : całkowita liczba obserwacji w zbiorze danych
W tym przykładzie obliczamy SST w następujący sposób: (64,2667)(15-1) = 899,7
Krok 2: Oblicz SSB
Następnie obliczymy sumę kwadratów (SSB), którą można znaleźć korzystając ze wzoru:
SSB = Σn jot ( x j – x suma ) 2
Złoto:
- Σ : grecki symbol oznaczający „sumę”
- n j : całkowita liczba obserwacji w j- tej grupie
- x j : średnia j -tej grupy
- x suma : średnia wszystkich danych
W tym przykładzie obliczamy SSB w następujący sposób: (5)(26,4-22,533) 2 +(5)(25,6-22,533) 2 + (5)(15,6-22,533) 2 = 362,1
Krok 3: Oblicz SSS.
Następnie obliczymy przedmiotową sumę kwadratów (SSS), którą można znaleźć korzystając ze wzoru:
SSS =(Σr 2 k /c) – (N 2 /rc)
Złoto:
- Σ : grecki symbol oznaczający „sumę”
- r 2 k : kwadratowa suma k- tego pacjenta
- N: suma wszystkich danych
- r: całkowita liczba pacjentów
- c: całkowita liczba grup
W tym przykładzie obliczamy SSS w następujący sposób: ((74 2 + 42 2 + 62 2 + 92 2 + 68 2 )/3) – (338 2 /(5)(3)) = 441,1
Krok 4: Oblicz SES.
Następnie obliczymy sumę kwadratu błędu (SSE), którą można obliczyć korzystając ze wzoru:
SSE = SST – SSB – SSS
W tym przykładzie obliczamy SES w następujący sposób: 899,7 – 362,1 – 441,1 = 96,5
Krok 5: Wypełnij tabelę ANOVA z powtarzanymi pomiarami.
Teraz, gdy mamy już SSB, SSS i SSE, możemy wypełnić tabelę ANOVA z powtarzanymi pomiarami:
| Źródło | Suma kwadratów (SS) | zm | Średnie kwadraty (MS) | F |
|---|---|---|---|---|
| Między | 362.1 | 2 | 181.1 | 15.006 |
| Temat | 441.1 | 4 | 110.3 | |
| Błąd | 96,5 | 8 | 12.1 |
Oto jak obliczyliśmy różne liczby w tabeli:
- df pomiędzy: #grupami – 1 = 3 – 1 = 2
- df temat: #uczestnicy – 1 = 5 – 1 = 4
- Błąd df: df pomiędzy * df temat = 2*4 = 8
- MS wchodzi: SSB / df wchodzi = 362,1 / 2 = 181,1
- Przedmiot stwardnienia rozsianego: Przedmiot SSS / df = 441,1 / 4 = 110,3
- Błąd MS: błąd SSE / df = 96,5 / 8 = 12,1
- F: MS wchodzi / błąd MS = 181,1 / 12,1 = 15,006
Krok 6: Interpretacja wyników.
Statystyka testu F dla tej jednokierunkowej ANOVA z powtarzanymi pomiarami wynosi 15,006 . Aby określić, czy jest to wynik istotny statystycznie, należy porównać go z krytyczną wartością F znalezioną w tabeli rozkładu F o następujących wartościach:
- α (poziom istotności) = 0,05
- DF1 (stopnie swobody licznika) = df pomiędzy = 2
- DF2 (stopnie swobody mianownika) = błąd df = 8
Ustalamy, że wartość krytyczna F wynosi 4,459 .
Ponieważ statystyka testu F w tabeli ANOVA jest większa niż wartość krytyczna F w tabeli rozkładu F, odrzucamy hipotezę zerową. Oznacza to, że mamy wystarczające dowody, aby stwierdzić, że istnieje statystycznie istotna różnica pomiędzy średnim czasem reakcji na leki.