Anova vs regresja: jaka jest różnica?
Dwa powszechnie stosowane modele w statystyce to modele ANOVA i modele regresji.
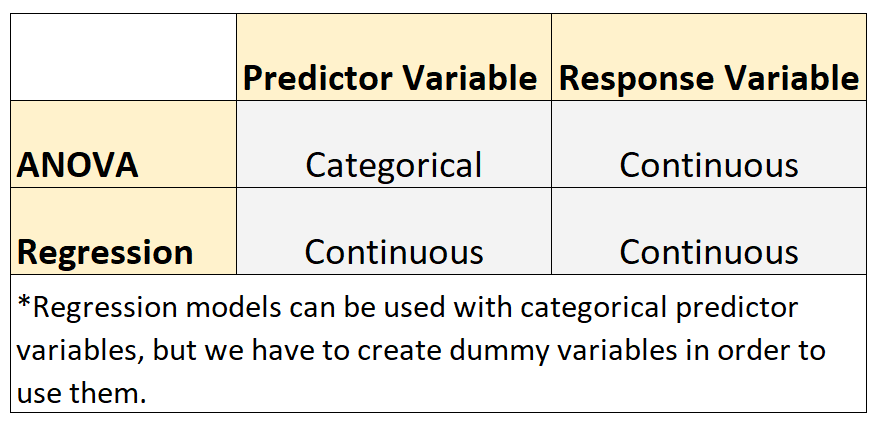
Te dwa typy modeli łączy następujące podobieństwo:
- Zmienna odpowiedzi w każdym modelu jest ciągła. Przykłady zmiennych ciągłych obejmują wagę, wzrost, długość, szerokość, czas, wiek itp.
Jednak te dwa typy modeli mają następującą różnicę :
- Modele ANOVA stosuje się, gdy zmienne predykcyjne są jakościowe. Przykładami zmiennych kategorycznych są poziom wykształcenia, kolor oczu, stan cywilny itp.
- Modele regresji stosuje się, gdy zmienne predykcyjne są ciągłe.*
*Modeli regresji można używać ze zmiennymi predykcyjnymi jakościowymi, ale aby z nich skorzystać, musimy utworzyć zmienne fikcyjne .
Poniższe przykłady pokazują, kiedy w praktyce należy stosować modele ANOVA lub modele regresji.
Przykład 1: Preferowany model ANOVA
Załóżmy, że biolog chce zrozumieć, czy cztery różne nawozy prowadzą do tego samego średniego wzrostu roślin (w calach) w okresie jednego miesiąca. Aby to sprawdzić, stosuje każdy nawóz do 20 roślin i po miesiącu rejestruje wzrost każdej rośliny.
W tym scenariuszu biolog musi zastosować jednokierunkowy model ANOVA do analizy różnic między nawozami, ponieważ istnieje zmienna predykcyjna i jest ona kategoryczna.
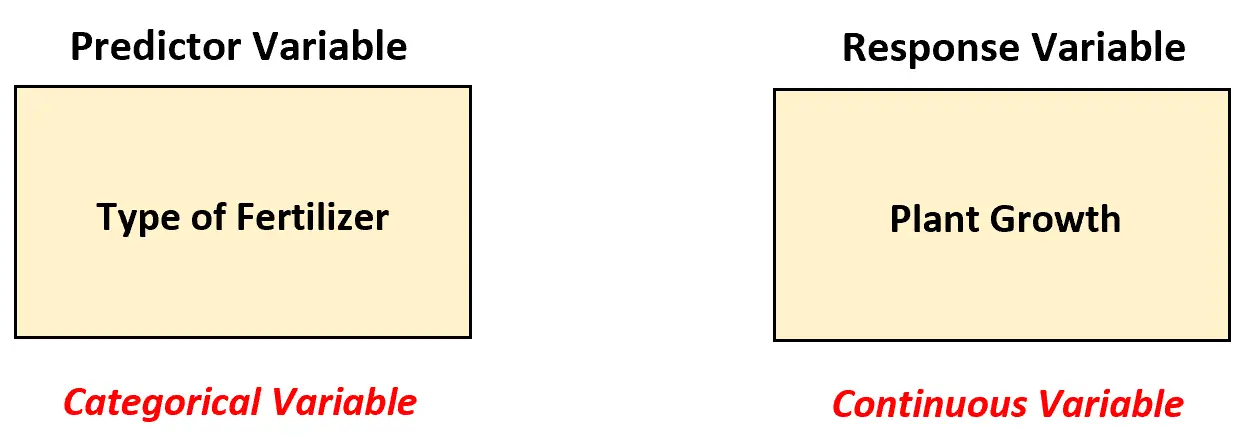
Innymi słowy, wartości zmiennej predykcyjnej można podzielić na następujące „kategorie”:
- Nawóz 1
- Nawóz 2
- Nawóz 3
- Nawóz 4
Jednoczynnikowa ANOVA powie biologowi, czy średni wzrost roślin jest równy w przypadku czterech różnych nawozów.
Przykład 2: Preferowany model regresji
Załóżmy, że agent nieruchomości chce zrozumieć związek między powierzchnią a ceną nieruchomości. Aby przeanalizować tę zależność, zbiera dane dotyczące powierzchni i ceny 200 domów w danym mieście.
W tym scenariuszu pośrednik w obrocie nieruchomościami powinien zastosować prosty model regresji liniowej do analizy związku między tymi dwiema zmiennymi, ponieważ zmienna predykcyjna (powierzchnia kwadratowa) jest ciągła.
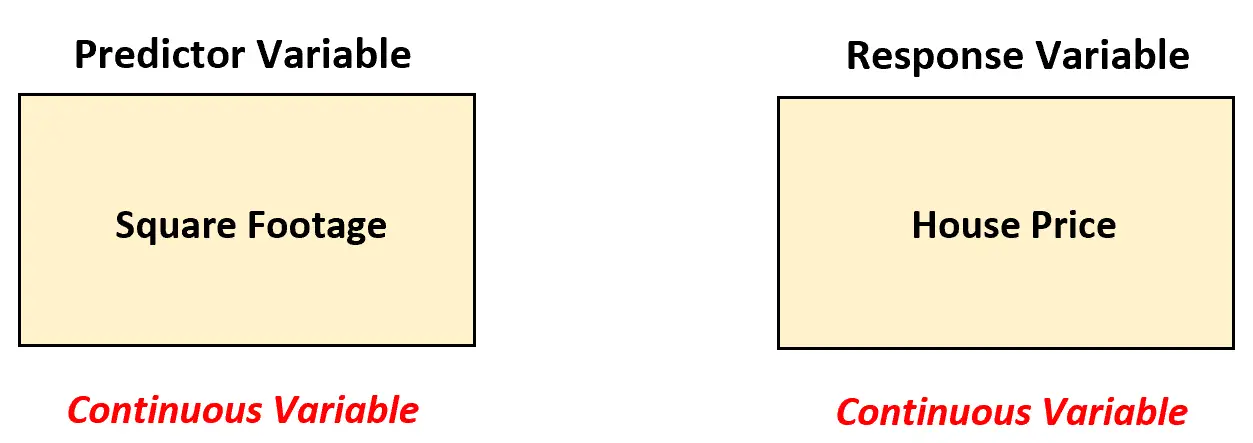
Stosując prostą regresję liniową, agent nieruchomości może dopasować następujący model regresji:
Cena nieruchomości = β 0 + β 1 (powierzchnia kwadratowa)
Wartość β 1 będzie reprezentować średnią zmianę ceny domu związaną z każdą dodatkową stopą kwadratową.
Umożliwi to agentowi nieruchomości ilościowe określenie związku między powierzchnią powierzchni a ceną nieruchomości.
Przykład 3: Model regresji z preferowanymi zmiennymi fikcyjnymi
Załóżmy, że agent nieruchomości chce zrozumieć związek pomiędzy zmiennymi predykcyjnymi „powierzchnia kwadratowa” i „typ domu” (jednorodzinny, mieszkanie, kamienica) ze zmienną odpowiedzi – ceną nieruchomości.
W tym scenariuszu agent nieruchomości może zastosować wielokrotną regresję liniową, konwertując „typ domu” na zmienną fikcyjną, ponieważ obecnie jest to zmienna kategoryczna.
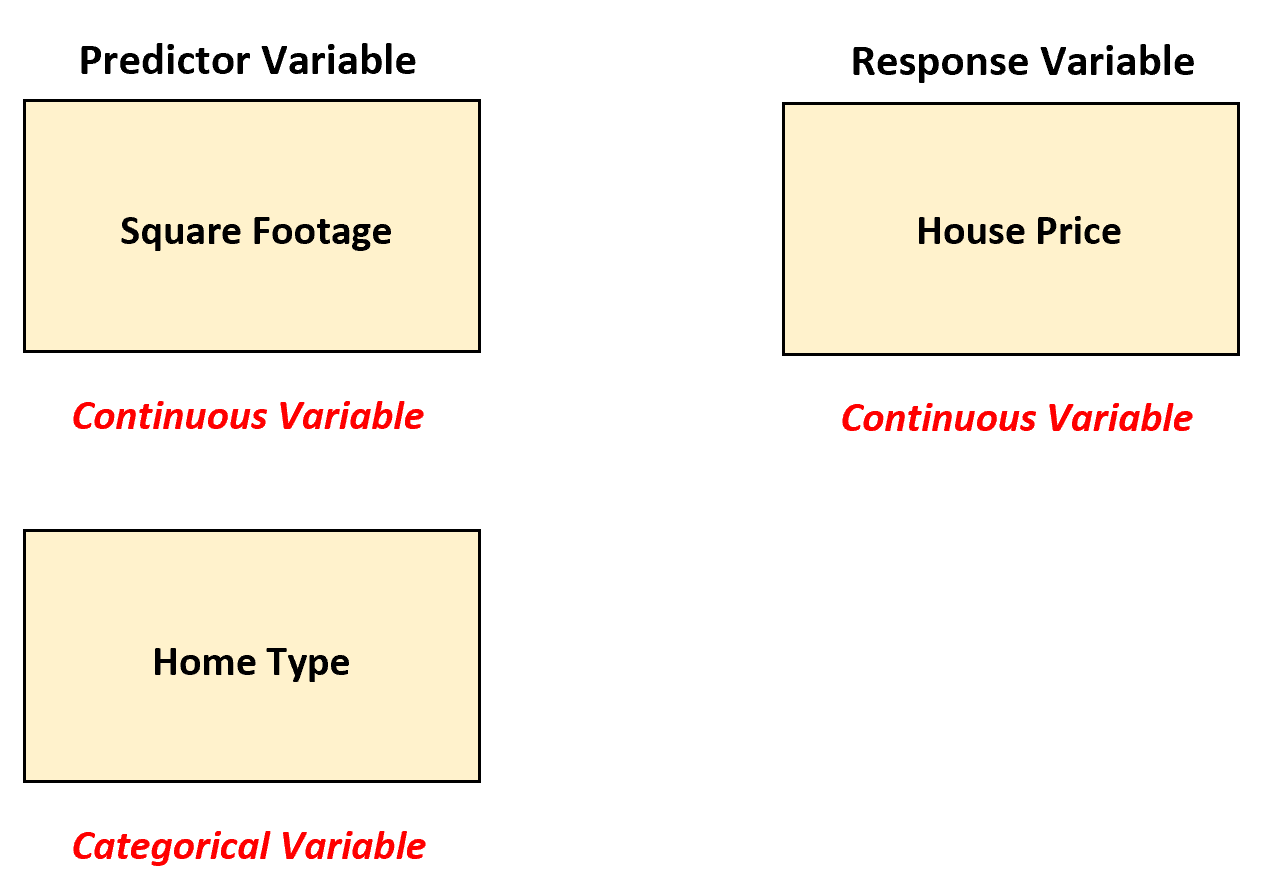
Agent nieruchomości może następnie dopasować następujący model regresji liniowej:
Cena nieruchomości = β 0 + β 1 (powierzchnia kwadratowa) + β 2 (jednorodzinna) + β 3 (mieszkanie)
Oto jak interpretujemy współczynniki modelu:
- β 1 : Średnia zmiana ceny domu związana z jedną dodatkową stopą kwadratową.
- β 2 : Średnia różnica w cenie pomiędzy domem jednorodzinnym a kamienicą, przy założeniu, że powierzchnia użytkowa pozostaje stała.
- β 3 : Średnia różnica w cenie pomiędzy domem jednorodzinnym a mieszkaniem, przy założeniu stałej powierzchni.
Zapoznaj się z poniższymi samouczkami, aby dowiedzieć się, jak tworzyć zmienne fikcyjne w różnych programach statystycznych:
Dodatkowe zasoby
Poniższe samouczki zapewniają szczegółowe wprowadzenie do modeli ANOVA:
Poniższe samouczki zawierają szczegółowe wprowadzenie do modeli regresji liniowej: