Rozkład bernoulliego i rozkład dwumianowy: jaka jest różnica?
Zmienna losowa ma rozkład Bernoulliego , jeśli ma tylko dwa możliwe wyniki: 0 lub 1.
Załóżmy na przykład, że rzucamy raz monetą. Niech p . Oznacza to, że prawdopodobieństwo wyrzucenia reszki wynosi 1- p .
Moglibyśmy więc napisać:
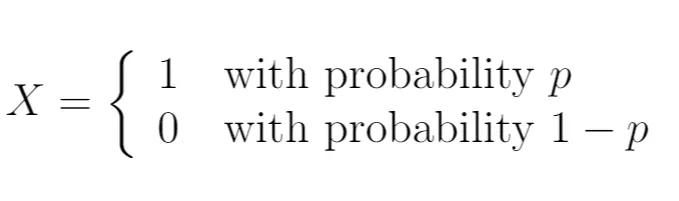
W tym przypadku zmienna losowa X ma rozkład Bernoulliego. Może przyjmować tylko dwie możliwe wartości.
Jeśli teraz rzucimy monetą wiele razy, suma zmiennych losowych Bernoulliego będzie miała rozkład dwumianowy.
Załóżmy na przykład, że rzucamy monetą 5 razy i chcemy poznać prawdopodobieństwo wyrzucenia orła k razy. Wygląda jak zmienna losowa
Jeśli zmienna losowa X ma rozkład dwumianowy, prawdopodobieństwo, że X = k powodzenia można obliczyć za pomocą następującego wzoru:
P(X=k) = n C k * p k * (1-p) nk
Złoto:
- n: liczba prób
- k: liczba sukcesów
- p: prawdopodobieństwo sukcesu w danej próbie
- n C k : liczba sposobów uzyskania k sukcesów w n próbach
Załóżmy na przykład, że rzucamy monetą 3 razy. Możemy użyć powyższego wzoru, aby określić prawdopodobieństwo uzyskania 0 reszek podczas tych 3 rzutów:
P(X=0) = 3 C 0 * 0,5 0 * (1-0,5) 3-0 = 1 * 1 * (0,5) 3 = 0,125
Gdy n = 1 próba, rozkład dwumianowy jest równoważny rozkładowi Bernoulliego.
Ważne notatki
Oto kilka ważnych uwag dotyczących rozkładu Bernoulliego i dwumianu:
1. Zmienna losowa podążająca za rozkładem Bernoulliego może przyjmować tylko dwie możliwe wartości, natomiast zmienna losowa podążająca za rozkładem dwumianowym może przyjmować kilka wartości.
Na przykład w jednym rzucie monetą wypadnie 0 lub 1 reszka. Jednak w serii 5 losowań możemy mieć 0, 1, 2, 3, 4 lub 5 orłów.
2. Aby zmienna losowa miała rozkład dwumianowy, prawdopodobieństwo „sukcesu” w każdej próbie Bernoulliego musi być równe i niezależne.
Na przykład, jeśli zdefiniujemy „sukces” jako lądowanie na orłach, to prawdopodobieństwo sukcesu w każdym rzucie wynosi 0,5, a każdy rzut jest niezależny – wynik jednego rzutu nie wpływa na wynik drugiego.
Dodatkowe zasoby
Wprowadzenie do eksperymentów dwumianowych
Wprowadzenie do rozkładu dwumianowego
Zrozumienie kształtu rozkładu dwumianowego
o autorze
Dr Benjamin Anderson
Cześć, jestem Benjamin i jestem emerytowanym profesorem statystyki, który został oddanym nauczycielem Statorials. Dzięki bogatemu doświadczeniu i wiedzy specjalistycznej w dziedzinie statystyki chętnie dzielę się swoją wiedzą, aby wzmocnić pozycję uczniów za pośrednictwem Statorials. Wiedzieć więcej