Skumulowana częstotliwość bezwzględna
W tym artykule wyjaśniono, czym jest skumulowana częstotliwość bezwzględna i do czego służy. Znajdziesz więc definicję skumulowanej częstotliwości bezwzględnej, sposób uzyskania skumulowanej częstotliwości bezwzględnej ze zbioru danych, a ponadto dwa ćwiczenia rozwiązane krok po kroku.
Co to jest skumulowana częstotliwość bezwzględna?
W statystyce skumulowana częstotliwość bezwzględna jest skumulowaną sumą częstotliwości bezwzględnych. Oznacza to, że skumulowana częstotliwość bezwzględna wartości jest równa częstotliwości bezwzględnej tej wartości plus częstotliwości bezwzględne wszystkich wartości mniejszych od niej.
Zwykle w statystyce wielka litera F z indeksem dolnym i jest używana do przedstawienia skumulowanej częstotliwości bezwzględnej wartości i , więc symbolem skumulowanej częstotliwości bezwzględnej jest Fi .
Logicznie rzecz biorąc, aby zrozumieć, co oznacza skumulowana częstotliwość bezwzględna, należy mieć jasność co do pojęcia częstotliwości bezwzględnej, dlatego przed kontynuowaniem wyjaśnień zaleca się sprawdzenie poniższego artykułu.
Jak obliczyć skumulowaną częstotliwość bezwzględną
Aby obliczyć skumulowaną częstotliwość bezwzględną, należy wykonać następujące kroki:
- Utwórz tabelę ze wszystkimi różnymi wartościami, które pojawiają się w zbiorze danych, to znaczy umieść każdą inną wartość w wierszu tabeli.
- Określa bezwzględną częstotliwość każdej wartości.
- Znajdź skumulowaną częstotliwość bezwzględną każdej wartości, którą oblicza się, dodając częstotliwość bezwzględną samej wartości plus częstotliwości bezwzględne wszystkich mniejszych wartości.
Należy pamiętać, że jeśli zmienna jest ciągła lub istnieje wiele różnych wartości, należy najpierw pogrupować dane w przedziały, a następnie zastosować kroki opisane powyżej, aby znaleźć skumulowaną częstotliwość bezwzględną.
Przykłady skumulowanej częstotliwości bezwzględnej
Aby zobaczyć, jak obliczana jest skumulowana częstotliwość bezwzględna, poniżej znajdują się dwa przykłady z życia wzięte, krok po kroku. W pierwszym przykładzie obliczono skumulowane częstotliwości bezwzględne zmiennej dyskretnej, a w drugim kroku zmiennej ciągłej.
Przykład 1: zmienna dyskretna
- Oceny uzyskane ze statystyki w klasie 30 uczniów przedstawiają się następująco. Jaka jest skumulowana częstotliwość bezwzględna każdej nuty?
![]()
![]()
![]()
Ponieważ wszystkie liczby mogą być tylko liczbami całkowitymi, jest to zmienna dyskretna. Nie jest zatem konieczne grupowanie danych w przedziały.
Aby więc określić skumulowaną częstotliwość bezwzględną, musimy najpierw znaleźć częstotliwość bezwzględną każdej wartości, czyli liczbę wystąpień każdej wartości w próbce statystycznej.

Teraz, gdy znamy częstotliwość bezwzględną, możemy obliczyć skumulowaną częstotliwość bezwzględną. Aby to zrobić, mamy dwie możliwości: albo dodajemy częstotliwość bezwzględną wartości plus wszystkie częstotliwości bezwzględne najmniejszych wartości, albo odwrotnie, dodajemy częstotliwość bezwzględną wartości plus skumulowaną częstotliwość bezwzględną poprzednich wartości . wartość.

W skrócie tabela z bezwzględną skumulowaną częstotliwością ćwiczeń wygląda następująco:

Należy pamiętać, że skumulowana częstotliwość bezwzględna ostatniej wartości zawsze odpowiada całkowitej liczbie danych. W przeciwnym razie oznacza to, że popełniłeś błąd w obliczeniach.
Przykład 2: zmienna ciągła
- Zmierzono wzrost 20 osób i uzyskano wyniki przedstawione poniżej. Dzieli dane na przedziały i oblicza skumulowaną częstotliwość bezwzględną dla każdego przedziału.
![]()
![]()
Rozkład w tym przykładzie jest ciągły, ponieważ mogą występować liczby dziesiętne, dlatego najlepiej jest pogrupować dane w różne przedziały.
Zatem dzielimy dane na przedziały i liczymy, ile razy w każdym przedziale pojawia się liczba, aby otrzymać częstotliwość bezwzględną:

Następnie, aby określić skumulowaną częstotliwość bezwzględną, wystarczy dodać częstotliwości bezwzględne wszystkich poprzednich wartości plus częstotliwość bezwzględną danej wartości:
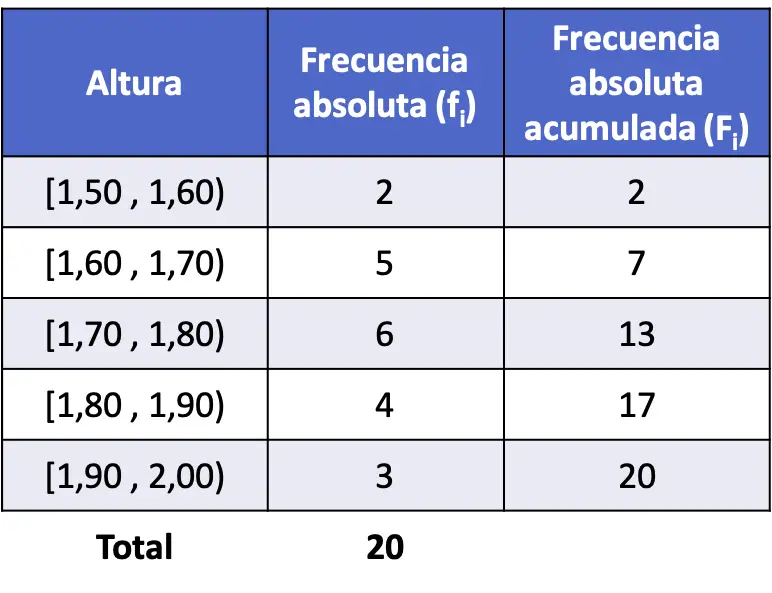
Skumulowana częstotliwość bezwzględna i skumulowana częstotliwość względna
Różnica między skumulowaną częstotliwością bezwzględną a skumulowaną częstotliwością względną odpowiada typowi częstotliwości skumulowanej. Skumulowana częstotliwość bezwzględna jest równa sumie częstotliwości bezwzględnych wartości równych lub niższych, natomiast skumulowana częstotliwość względna jest równoważna częstotliwościom względnym wartości równych lub niższych.
Zatem skumulowana częstotliwość bezwzględna jest obliczana na podstawie częstotliwości bezwzględnej, podczas gdy skumulowana częstotliwość względna jest obliczana na podstawie częstotliwości względnej.
Przykład obliczenia skumulowanej częstotliwości względnej można zobaczyć tutaj: