Binompdf vs binomcdf: różnica (plus przykłady)

Rozkład dwumianowy jest jednym z najczęściej używanych rozkładów we wszystkich statystykach.

Na kalkulatorze TI-84 możesz użyć dwóch funkcji do znalezienia prawdopodobieństw związanych z rozkładem dwumianowym:

• binompdf(n, p, x) : oblicza prawdopodobieństwo, że w ciągu n prób wystąpi dokładnie x sukcesów , przy czym prawdopodobieństwo sukcesu w danej próbie jest równe p .
• binomcdf(n, p, x) : oblicza prawdopodobieństwo, że w n próbach wystąpi x lub mniej sukcesów , przy czym prawdopodobieństwo sukcesu w danej próbie jest równe p .

Dostęp do każdej z tych funkcji można uzyskać w kalkulatorze TI-84, naciskając przycisk 2, a następnie naciskając VARS . Spowoduje to przejście do ekranu DISTR , na którym możesz użyć binompdf() i binomcdf() :

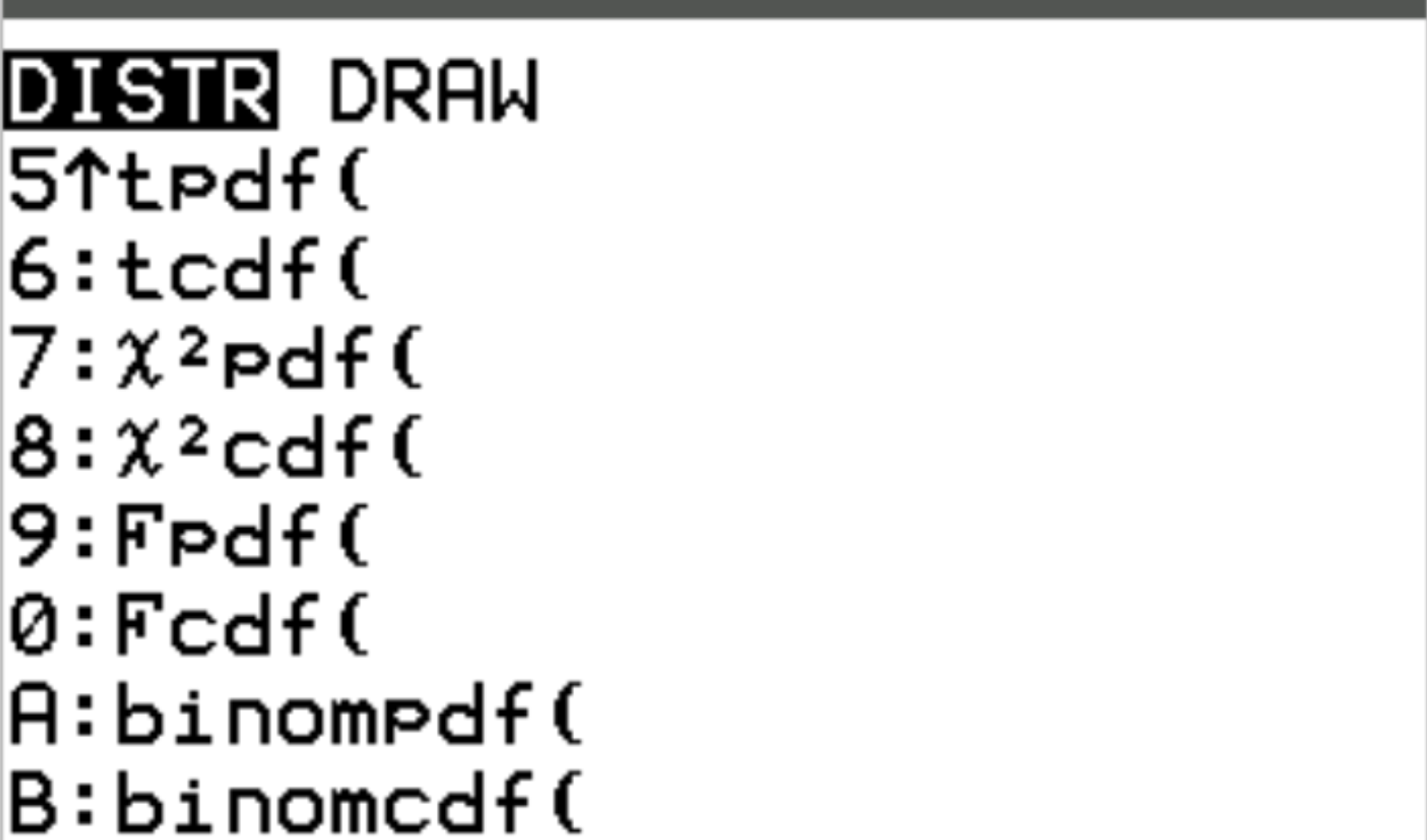
Poniższe przykłady pokazują, jak w praktyce wykorzystać każdą z tych funkcji.

Przykłady: Jak używać Binompdf()

Poniższe przykłady pokazują, jak używać funkcji binompdf() .

Przykład 1: Próby rzutów wolnych

Jessica wykonuje 80% swoich prób rzutów wolnych. Jeśli wykona 10 rzutów wolnych, jakie jest prawdopodobieństwo, że trafi dokładnie 7?

Aby odpowiedzieć na to pytanie, możemy wpisać następującą formułę:

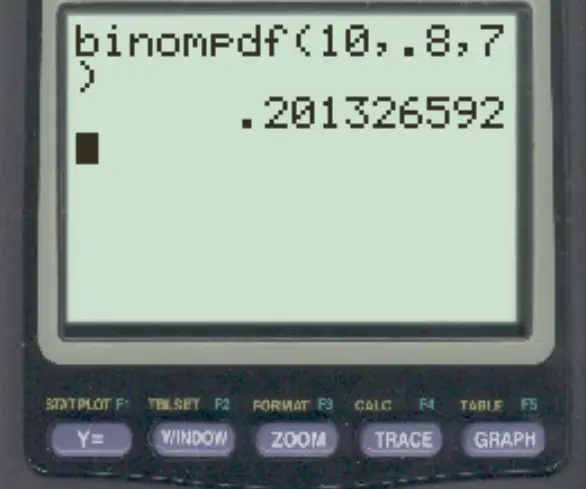
Prawdopodobieństwo, że wypadnie dokładnie 7, wynosi 0,2013 .

Przykład 2: Oszukańcze transakcje

Bank wie, że 3% wszystkich transakcji to oszustwa. Jeżeli danego dnia nastąpi 20 transakcji, jakie jest prawdopodobieństwo, że dokładnie 2 z nich będą fałszywe?

Aby odpowiedzieć na to pytanie, możemy wpisać następującą formułę:

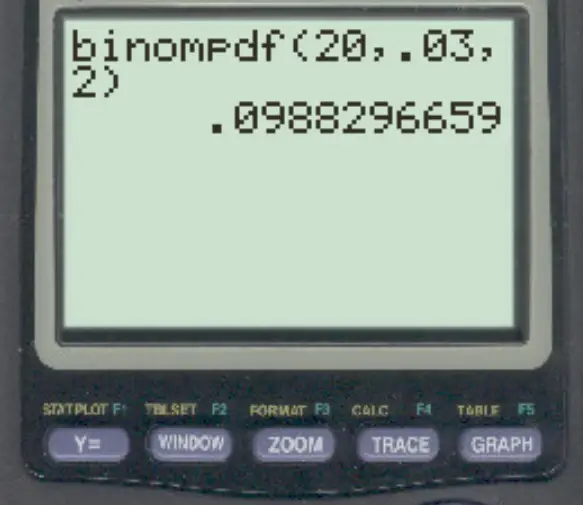
Prawdopodobieństwo, że dokładnie 2 transakcje są fałszywe, wynosi 0,0988 .

Przykłady: Jak używać Binomcdf()

Poniższe przykłady pokazują, jak używać funkcji binomcdf() .

Przykład 1: Próby rzutów wolnych

Jessica wykonuje 50% swoich prób rzutów wolnych. Jeśli wykona 10 rzutów wolnych, jakie jest prawdopodobieństwo, że trafi 7 lub mniej?

Aby odpowiedzieć na to pytanie, możemy wpisać następującą formułę:

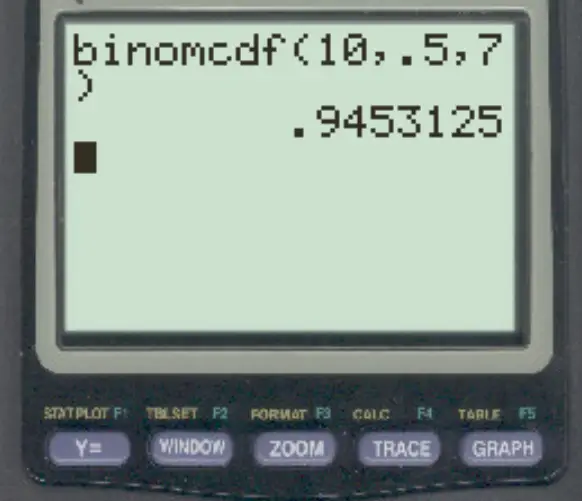
Prawdopodobieństwo, że wykona ona 7 lub mniej rzutów wolnych, wynosi 0,9453 .

Przykład 2: Oszukańcze transakcje

Bank wie, że 3% wszystkich transakcji to oszustwa. Jeśli danego dnia nastąpi 20 transakcji, jakie jest prawdopodobieństwo, że więcej niż 2 transakcje są fałszywe?

Aby odpowiedzieć na to pytanie, możemy wpisać następującą formułę:

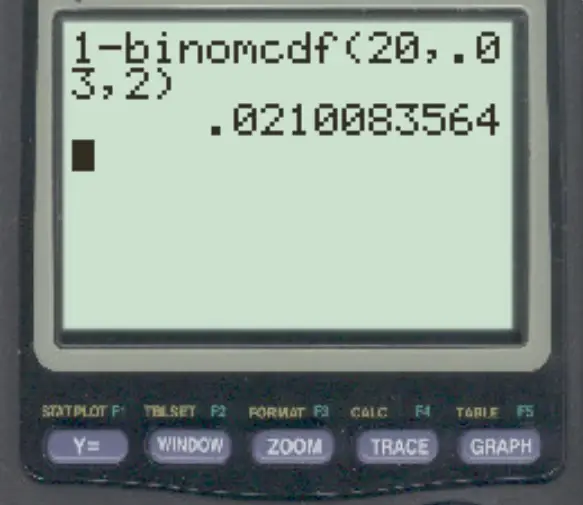
Prawdopodobieństwo, że więcej niż 2 transakcje są fałszywe, wynosi 0,021 .

Dodatkowe zasoby

Kalkulator rozkładu dwumianowego
Jak wykonać test dwumianowy w programie Excel