Jak uruchomić bootstrap w r (z przykładami)

Metoda ładowania początkowego to metoda, której można użyć do oszacowania błędu standardowego dowolnej statystyki i ustalenia przedziału ufności dla tej statystyki.

Podstawowy proces ładowania początkowego jest następujący:

• Pobierz k powtórzonych próbek z zamianą z danego zbioru danych.
• Dla każdej próbki oblicz interesującą statystykę.
• Daje to k różnych szacunków dla danej statystyki, które można następnie wykorzystać do obliczenia błędu standardowego statystyki i utworzenia przedziału ufności dla tej statystyki.

Możemy wykonać bootstrap w R, korzystając z następujących funkcji z biblioteki bootstrap :

1. Wygeneruj próbki bootstrap.

boot(dane, statystyki, R, …)

Złoto:

• dane: wektor, macierz lub blok danych
• statystyka: funkcja generująca statystykę, która ma zostać zainicjowana
• Odp.: Liczba powtórzeń bootstrapu

2. Wygeneruj przedział ufności ładowania początkowego.

boot.ci (obiekt startowy, konf, typ)

Złoto:

• bootobject: Obiekt zwracany przez funkcję boot().
• conf: Przedział ufności do obliczenia. Wartość domyślna to 0,95
• type: Typ przedziału ufności do obliczenia. Opcje obejmują „standard”, „podstawowy”, „stud”, „perc”, „bca” i „all” – domyślnie jest to „all”

Poniższe przykłady pokazują, jak wykorzystać te funkcje w praktyce.

Przykład 1: bootstrap pojedynczej statystyki

Poniższy kod pokazuje, jak obliczyć błąd standardowy dla kwadratu R prostego modelu regresji liniowej:

 set.seed(0)
library (boot)

#define function to calculate R-squared
rsq_function <- function (formula, data, indices) {
  d <- data[indices,] #allows boot to select sample
  fit <- lm(formula, data=d) #fit regression model
  return (summary(fit)$r.square) #return R-squared of model
}
#perform bootstrapping with 2000 replications
reps <- boot(data=mtcars, statistic=rsq_function, R=2000, formula=mpg~disp)

#view results of boostrapping
reps

ORDINARY NONPARAMETRIC BOOTSTRAP


Call:
boot(data = mtcars, statistic = rsq_function, R = 2000, formula = mpg ~ 
    available)


Bootstrap Statistics:
     original bias std. error
t1* 0.7183433 0.002164339 0.06513426

Z wyników możemy zobaczyć:

• Szacowany współczynnik R-kwadrat dla tego modelu regresji wynosi 0,7183433 .
• Błąd standardowy tego oszacowania wynosi 0,06513426 .

Możemy również szybko wizualizować rozkład próbek ładowanych metodą ładowania początkowego:

 plot(reps)

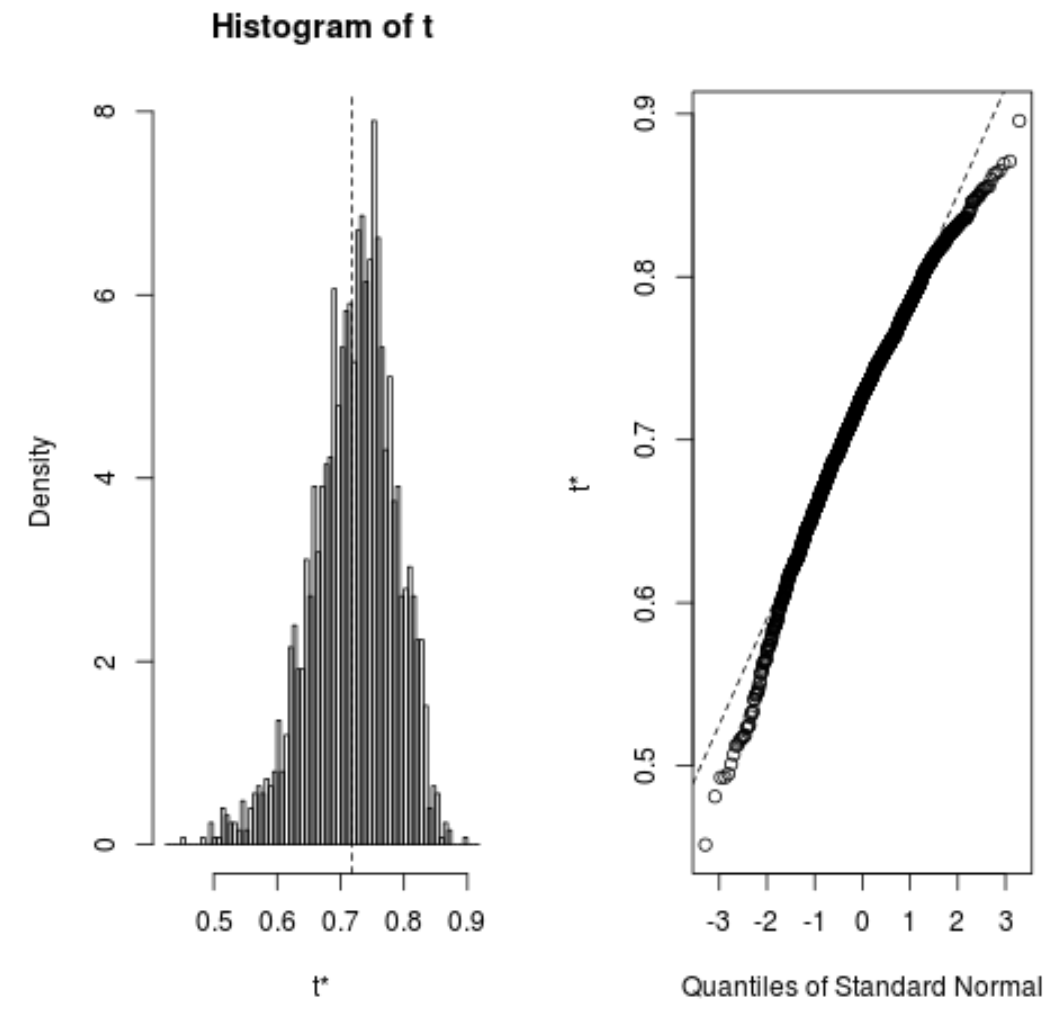
Możemy również użyć poniższego kodu, aby obliczyć 95% przedział ufności dla szacowanego kwadratu R modelu:

 #calculate adjusted bootstrap percentile (BCa) interval
boot.ci(reps, type=" bca ")

CALL: 
boot.ci(boot.out = reps, type = "bca")

Intervals: 
Level BCa          
95% (0.5350, 0.8188)  
Calculations and Intervals on Original Scale

Z wyniku widzimy, że bootstrapowy 95% przedział ufności dla prawdziwych wartości R-kwadrat wynosi (0,5350, 0,8188).

Przykład 2: ładowanie wielu statystyk

Poniższy kod pokazuje, jak obliczyć błąd standardowy dla każdego współczynnika w modelu wielokrotnej regresji liniowej:

 set.seed(0)
library (boot)

#define function to calculate fitted regression coefficients
coef_function <- function (formula, data, indices) {
  d <- data[indices,] #allows boot to select sample
  fit <- lm(formula, data=d) #fit regression model
  return (coef(fit)) #return coefficient estimates of model
}

#perform bootstrapping with 2000 replications
reps <- boot(data=mtcars, statistic=coef_function, R=2000, formula=mpg~disp)

#view results of boostrapping
reps

ORDINARY NONPARAMETRIC BOOTSTRAP


Call:
boot(data = mtcars, statistic = coef_function, R = 2000, formula = mpg ~ 
    available)


Bootstrap Statistics:
       original bias std. error
t1* 29.59985476 -5.058601e-02 1.49354577
t2* -0.04121512 6.549384e-05 0.00527082

Z wyników możemy zobaczyć:

• Oszacowany współczynnik wyrazu wolnego modelu wynosi 29,59985476 , a błąd standardowy tego oszacowania wynosi 1,49354577 .
• Oszacowany współczynnik dla zmiennej predykcyjnej disp w modelu wynosi -0,04121512 , a błąd standardowy tego oszacowania wynosi 0,00527082 .

Możemy również szybko wizualizować rozkład próbek ładowanych metodą bootstrap:

 plot(reps, index=1) #intercept of model
plot(reps, index=2) #disp predictor variable

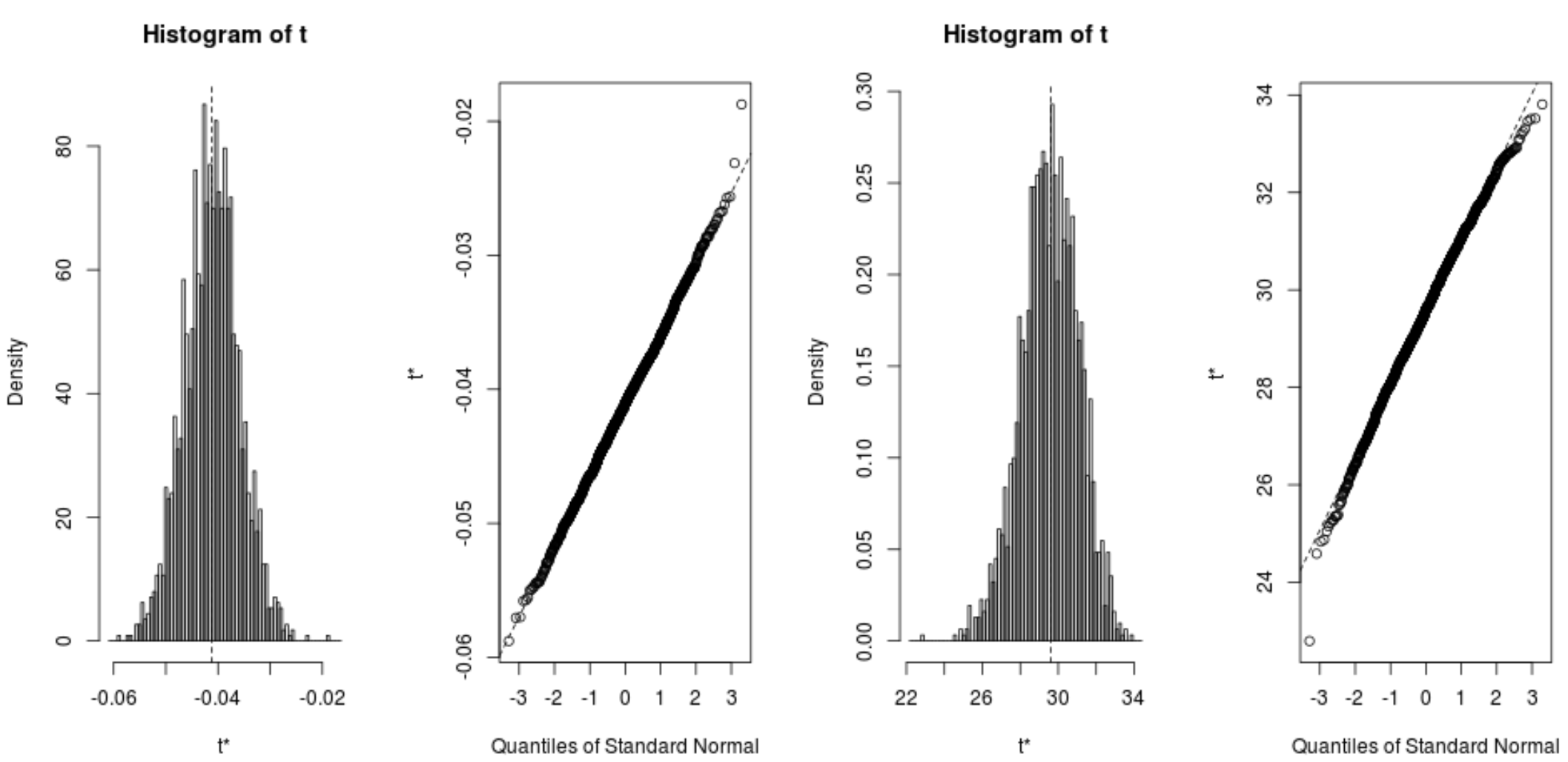
Możemy również użyć poniższego kodu do obliczenia 95% przedziałów ufności dla każdego współczynnika:

 #calculate adjusted bootstrap percentile (BCa) intervals
boot.ci(reps, type=" bca ", index=1) #intercept of model
boot.ci(reps, type=" bca ", index=2) #disp predictor variable

CALL: 
boot.ci(boot.out = reps, type = "bca", index = 1)

Intervals: 
Level BCa          
95% (26.78, 32.66)  
Calculations and Intervals on Original Scale
BOOTSTRAP CONFIDENCE INTERVAL CALCULATIONS
Based on 2000 bootstrap replicates

CALL: 
boot.ci(boot.out = reps, type = "bca", index = 2)

Intervals: 
Level BCa          
95% (-0.0520, -0.0312)  
Calculations and Intervals on Original Scale

Z wyników widać, że bootstrapowe 95% przedziały ufności dla współczynników modelu są następujące:

• IC dla przechwytywania: (26,78, 32,66)
• CI dla disp : (-.0520, -.0312)

Dodatkowe zasoby

Jak wykonać prostą regresję liniową w R
Jak wykonać wielokrotną regresję liniową w R
Wprowadzenie do przedziałów ufności