Jak obliczyć odmienność braya-curtisa w r

Odmienność Braya-Curtisa to sposób pomiaru odmienności między dwoma różnymi miejscami.

Jest często stosowany w ekologii i biologii do ilościowego określenia różnicy między dwoma stanowiskami pod względem gatunków występujących na tych stanowiskach.

Oblicza się go w następujący sposób:

BC _ij = 1 – (2*C _ij ) / (S _ja + S _jot )

Złoto:

• C _ij : Suma najniższych wartości dla gatunku znalezionego w każdym miejscu.
• S _i : Całkowita liczba próbek zliczonych w ośrodku i
• _Sj : Całkowita liczba okazów zliczonych na stanowisku j

Odmienność Braya-Curtisa zawsze mieści się w przedziale od 0 do 1, gdzie:

• Wartość 0 oznacza, że dwa miejsca nie różnią się od siebie. Innymi słowy, mają dokładnie taką samą liczbę gatunków każdego rodzaju.
• 1 wskazuje, że dwa miejsca wykazują całkowitą odmienność. Innymi słowy, nie mają żadnego gatunku tego samego typu.

Załóżmy na przykład, że botanik wychodzi i liczy pięć różnych gatunków roślin (A, B, C, D i E) w dwóch różnych miejscach.

Poniższa tabela podsumowuje zebrane dane:

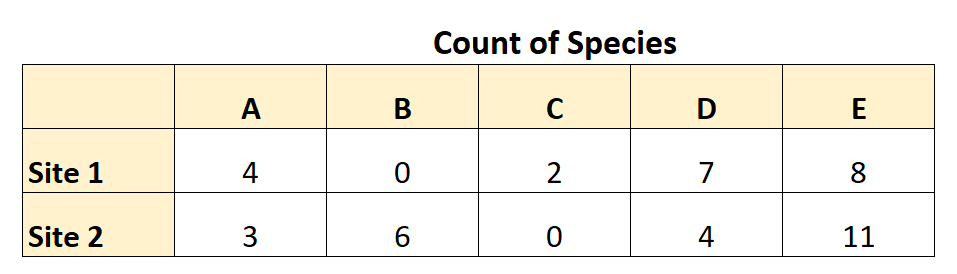
Korzystając z tych danych, może obliczyć odmienność Braya-Curtisa w następujący sposób:

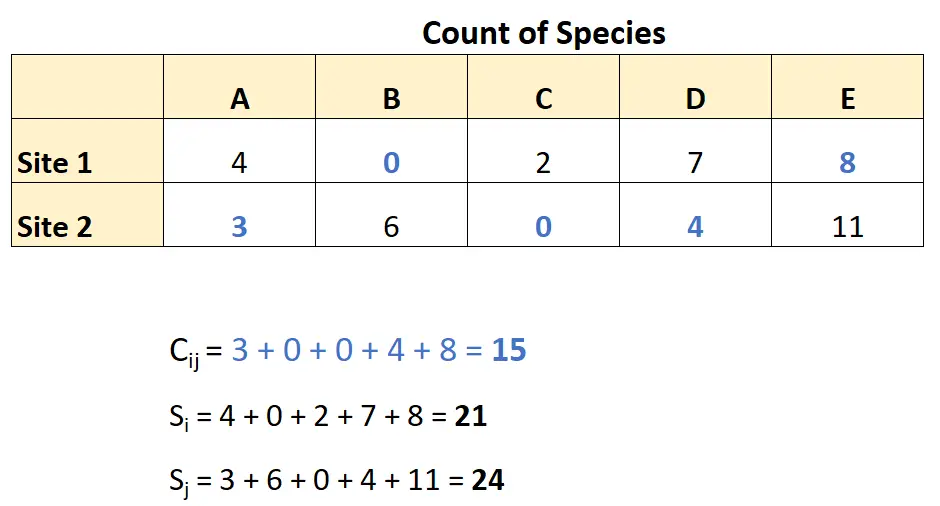
Całkując te liczby we wzorze na odmienność Braya-Curtisa, otrzymujemy:

• BC _ij = 1 – (2*C _ij ) / (S _ja + S _jot )
• BC _ij = 1 – (2*15) / (21 + 24)
• BC _ij = 0,33

Odmienność Braya-Curtisa pomiędzy tymi dwoma miejscami wynosi 0,33 .

Poniższy przykład pokazuje, jak obliczyć odmienność Braya-Curtisa w R.

Przykład: obliczenie odmienności Braya-Curtisa w R

Najpierw utwórzmy następującą ramkę danych w R, aby przechowywać nasze wartości danych:

 #create data frame
df <- data. frame (A=c(4, 3),
                 B=c(0, 6),
                 C=c(2, 0),
                 D=c(7, 4),
                 E=c(8, 11))

#view data frame
df

  A B C D E
1 4 0 2 7 8
2 3 6 0 4 11

Możemy użyć następującego kodu do obliczenia odmienności Braya-Curtisa między dwoma wierszami w ramce danych:

 #calculate Bray–Curtis dissimilarity
sum( apply (df, 2, function (x) abs ( max (x)- min (x)))) / sum ( rowSums (df))

[1] 0.3333333

Bray-Curtis okazuje się być inny i wynosi 0,33 .

Odpowiada to wartości, którą obliczyliśmy wcześniej ręcznie.

Uwaga : ta formuła będzie działać tylko wtedy, gdy każdy wiersz w ramce danych reprezentuje osobną witrynę.

Dodatkowe zasoby

Poniższe samouczki wyjaśniają, jak obliczyć inne metryki podobieństwa w R:

Jak obliczyć podobieństwo Jaccarda w R
Jak obliczyć podobieństwo cosinus w R