Jak używać normalnego cdf w r (z przykładami)

Do pracy z normalnym CDF (funkcją rozkładu skumulowanego) w R można użyć następujących metod:

Metoda 1: Oblicz normalne prawdopodobieństwa CDF

 #calculate probability that random value is less than 1.96 in normal CDF
pnorm(1.96)

#calculate probability that random value is greater than 1.96 in normal CDF
pnorm(1.96, lower.tail = FALSE )

Metoda 2: Wykreśl normalny CDF

 #define sequence of x-values
x <- seq(-4, 4, .01)

#calculate normal CDF probabilities
prob <- pnorm(x)
 
#normal plot CDF
plot(x, prob, type=" l ")

Poniższe przykłady pokazują, jak zastosować te metody w praktyce.

Przykład 1: Oblicz normalne prawdopodobieństwa CDF

Poniższy kod pokazuje, jak obliczyć prawdopodobieństwo, że zmienna losowa przyjmie wartość mniejszą niż 1,96 w standardowym rozkładzie normalnym:

 #calculate probability that random value is less than 1.96 in normal CDF
pnorm(1.96)

[1] 0.9750021

Prawdopodobieństwo, że zmienna losowa przyjmie wartość mniejszą niż 1,96 w standardowym rozkładzie normalnym, wynosi 0,975 .

Prawdopodobieństwo, że zmienna losowa przyjmie wartość większą niż 1,96, możemy również obliczyć, korzystając z argumentu less.tail :

 #calculate probability that random value is greater than 1.96 in normal CDF
pnorm(1.96, lower.tail = FALSE )

[1] 0.0249979

Możemy użyć następującej składni, aby znaleźć prawdopodobieństwo, że zmienna losowa przyjmie wartość pomiędzy dwiema wartościami w standardowym rozkładzie normalnym:

 #calculate probability that random value takes on value between -1.96 and 1.96
pnorm(1.96) - pnorm(-1.96)

[1] 0.9500042

Prawdopodobieństwo, że zmienna losowa przyjmie wartość od -1,96 do 1,96 w standardowym rozkładzie normalnym, wynosi 0,95 .

Przykład 2: Wykreślanie normalnego CDF

Poniższy kod pokazuje, jak wykreślić normalny CDF:

 #define sequence of x-values
x <- seq(-4, 4, .01)

#calculate normal CDF probabilities
prob <- pnorm(x)
 
#normal plot CDF
plot(x, prob, type=" l ") 

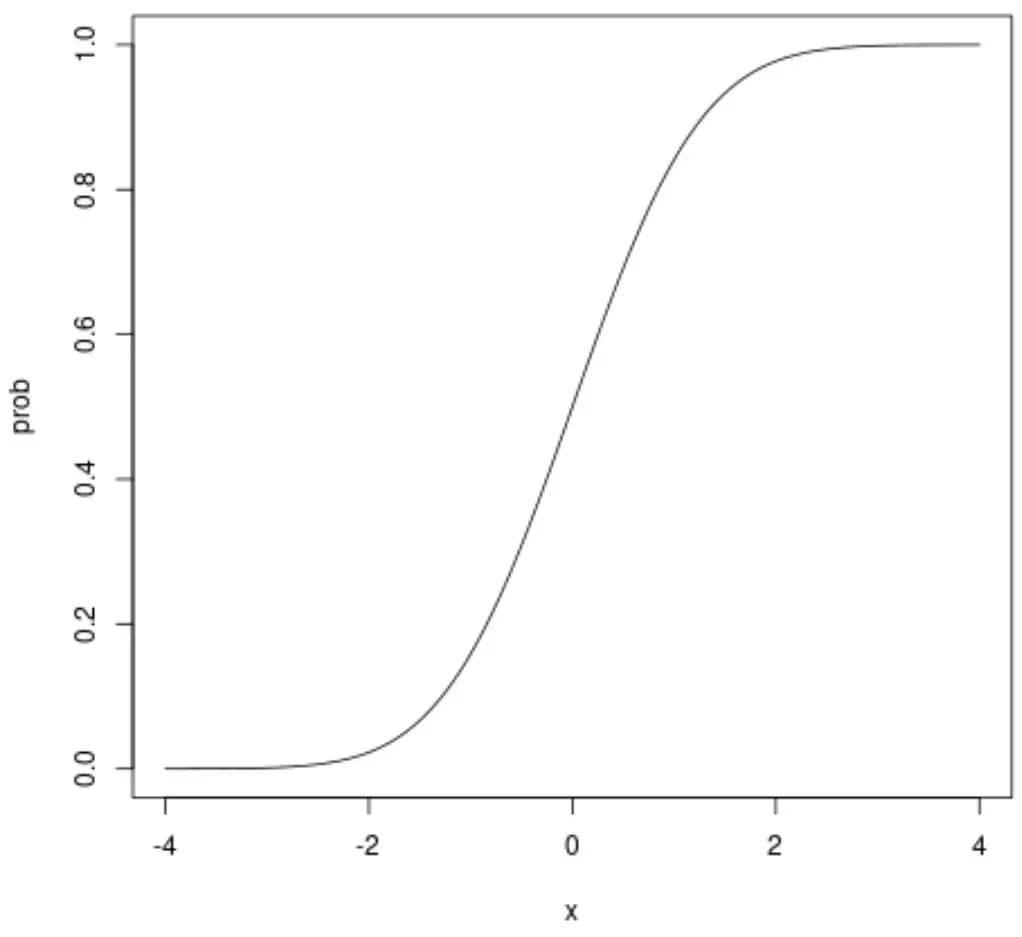
Oś x pokazuje wartości zmiennej losowej zgodnej ze standardowym rozkładem normalnym, a oś y pokazuje prawdopodobieństwo, że zmienna losowa przyjmie wartość mniejszą niż wartość pokazana na osi x.

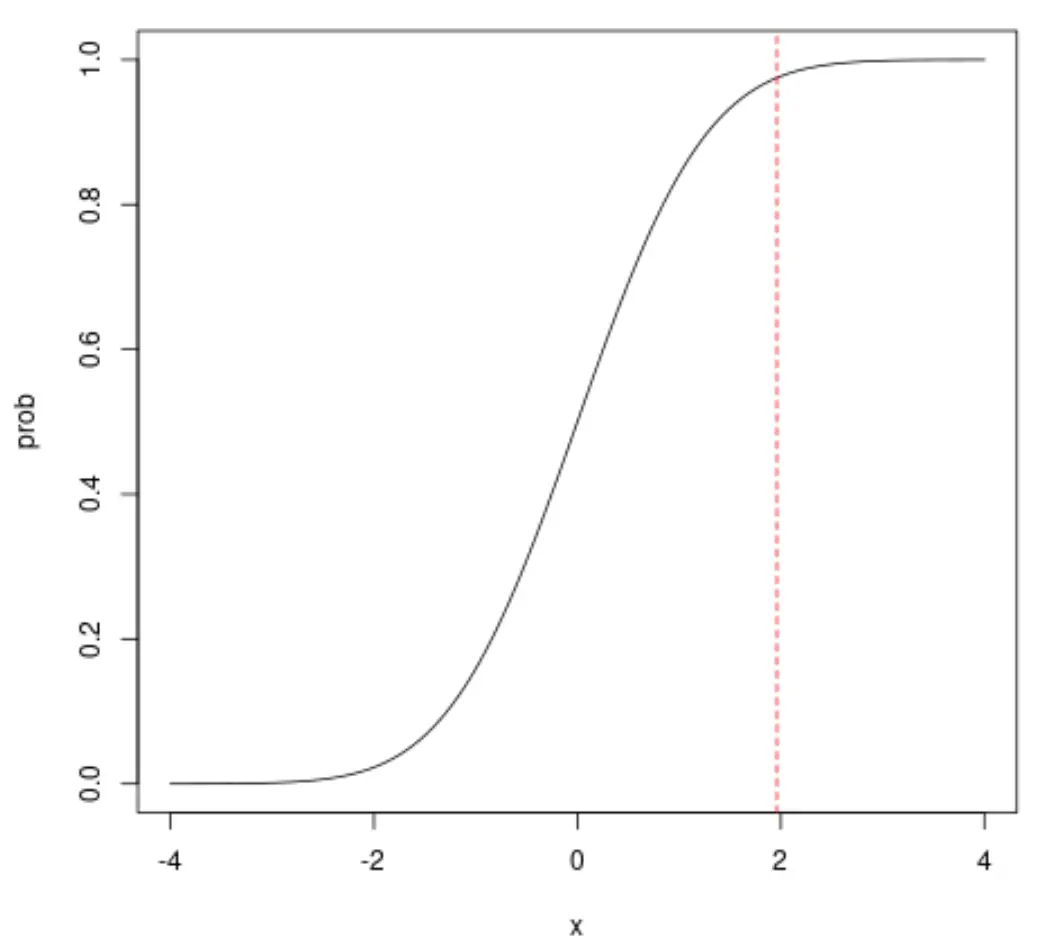
Na przykład, jeśli spojrzymy na x = 1,96, zobaczymy, że skumulowane prawdopodobieństwo, że x jest mniejsze niż 1,96, wynosi około 0,975:

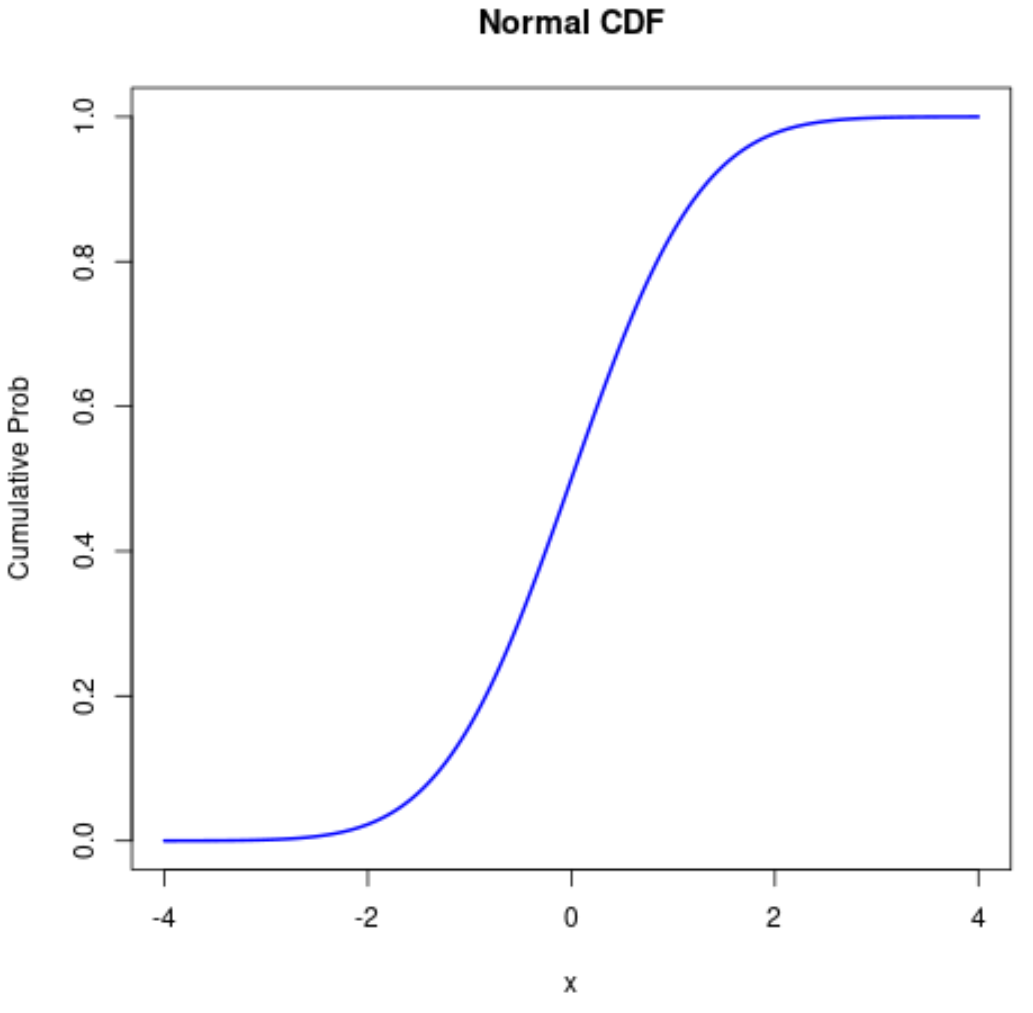
Pamiętaj, że możesz także zmienić estetykę normalnego wykresu CDF:

 #define sequence of x-values
x <- seq(-4, 4, .01)

#calculate normal CDF probabilities
prob <- pnorm(x)
 
#normal plot CDF
plot(x, prob, type=' l ', col=' blue ', lwd= 2 , main=' Normal CDF ', ylab=' Cumulative Prob ') 

Powiązane: Jak używać funkcji seq w R

Dodatkowe zasoby

Poniższe samouczki wyjaśniają, jak wykonywać inne typowe operacje w języku R:

Jak wykreślić rozkład normalny w R
Jak obliczyć wyniki Z w R
Przewodnik po dnorm, pnorm, qnorm i rnorm w R