Centralne twierdzenie graniczne

W tym artykule wyjaśniono, czym jest centralne twierdzenie graniczne (CLT) i do czego służy w statystyce. Znajdziesz tu także jaki jest wzór centralnego twierdzenia granicznego oraz rozwiązany krok po kroku przykład jego zastosowania.

Co to jest centralne twierdzenie graniczne?

W statystyce centralne twierdzenie graniczne , zwane także centralnym twierdzeniem granicznym , stwierdza, że rozkład średnich z próby zbliża się do rozkładu normalnego w miarę wzrostu wielkości próby, niezależnie od rozkładu prawdopodobieństwa populacji.

Oznacza to, że centralne twierdzenie graniczne mówi, że jeśli weźmiemy wystarczająco dużą liczbę próbek, średnią z tych próbek można przybliżyć do rozkładu normalnego.

Ponadto centralne twierdzenie graniczne stwierdza, że średnia próbki będzie zbliżać się do wartości średniej populacji w miarę wzrostu wielkości próby. Pozwala to na przybliżenie parametrów populacji statystycznej. Poniżej zobaczymy, jak to się robi.

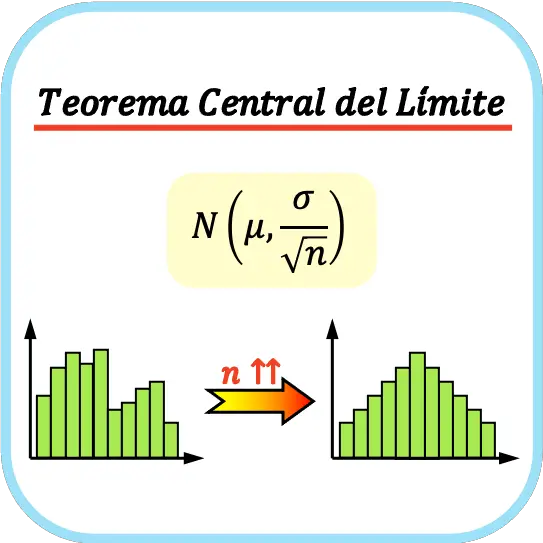
Ogólnie uważa się, że aby zastosować centralne twierdzenie graniczne, wielkość próby musi wynosić co najmniej 30 obserwacji, chociaż zależy to od charakterystyki badanej zmiennej.

Centralne twierdzenie graniczne ma wiele zastosowań, ponieważ rozkład normalny pozwala na wnioskowanie statystyczne, takie jak testowanie hipotez lub przedziały ufności. Na przykład w finansach centralne twierdzenie graniczne służy do analizy zwrotu i ryzyka inwestycji.

Przykład centralnego twierdzenia granicznego

Kiedy już poznaliśmy definicję centralnego twierdzenia granicznego, spójrzmy na przykład, aby w pełni zrozumieć jego znaczenie.

Przykładem centralnego twierdzenia granicznego jest rzut kostką. Rzut kostką ma dyskretny, równomierny rozkład , ponieważ wszystkie wyniki są jednakowo prawdopodobne. Jednak rozkład sumy kilku wyników zbliża się do rozkładu normalnego.

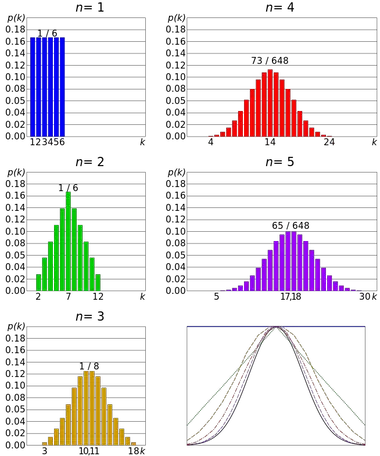
Zatem im więcej rzutów, tym większe prawdopodobieństwo, że kształt rozkładu średnich będzie przypominał wykres rozkładu normalnego.

Wzór centralnego twierdzenia granicznego

Centralne twierdzenie graniczne stwierdza, że jeśli populacja ma średnią μ i odchylenie standardowe σ i pobieramy odpowiednio dużą liczbę próbek (n≥30), to zbiór średnich z próby można aproksymować do rozkładu normalnego ze średnią μ i odchyleniem standardowym σ /√n.

Ponadto , _jeśli X _{1 ,} do rozkładu normalnego określonego wzorem:

Rozwiązane ćwiczenie centralnego twierdzenia granicznego

Abyś mógł w pełni przyswoić sobie tę koncepcję, oto rozwiązane ćwiczenie centralnego twierdzenia granicznego.

• Firma sprzedaje części używane do zastąpienia niektórych elementów zabawek. Moneta ma średnią masę 300 g i odchylenie standardowe 50 g. Jeżeli klient zamówił partię 100 sztuk, jakie jest prawdopodobieństwo, że średnia waga sztuk w partii będzie większa niż 305 g? A jakie jest prawdopodobieństwo, że partia 100 sztuk waży więcej niż 31 kg?

Ponieważ wielkość partii jest duża (n=100), do rozwiązania problemu możemy zastosować centralne twierdzenie graniczne.

Zatem korzystając ze wzoru centralnego twierdzenia granicznego, rozkład średnich z próbki można przybliżyć do rozkładu normalnego o następujących parametrach:

Teraz przeprowadzamy proces wpisywania, abyśmy mogli znaleźć prawdopodobieństwo, o jakie prosi nas ćwiczenie. Aby to zrobić, musimy odjąć średnią od rozkładu, a następnie podzielić przez odchylenie standardowe:

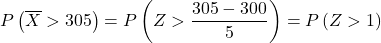tabela rozkładu normalnego :

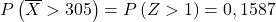
Powtarzamy więc proces pisania, a następnie znajdujemy drugie prawdopodobieństwo, że problem nas zadaje:

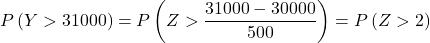
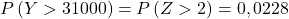➤ Zobacz: Prawo wielkich liczb