Jak zastosować centralne twierdzenie graniczne w kalkulatorze ti-84

Centralne twierdzenie graniczne stwierdza, że rozkład próbkowania średniej próbki jest w przybliżeniu normalny, jeśli wielkość próby jest wystarczająco duża, nawet jeśli rozkład populacji nie jest normalny.

Centralne twierdzenie graniczne stwierdza również, że rozkład próbkowania będzie miał następujące właściwości:

1. Średnia rozkładu próby będzie równa średniej rozkładu populacji:

x = µ

2. Odchylenie standardowe rozkładu próby będzie równe odchyleniu standardowemu populacji podzielonemu przez liczebność próby:

s = σ / √n

Aby znaleźć prawdopodobieństwa związane ze średnią próbki na kalkulatorze TI-84, możemy użyć funkcji normalcdf() o następującej składni:

 normalcdf (lower value, upper value, x , s/√ n )

Złoto:

• x : średnia próbki
• s : odchylenie standardowe próbki
• n : wielkość próbki

Aby uzyskać dostęp do tej funkcji w kalkulatorze TI-84, po prostu naciśnij 2nd , następnie naciśnij VARS i przewiń do normalcdf ( i naciśnij ENTER .

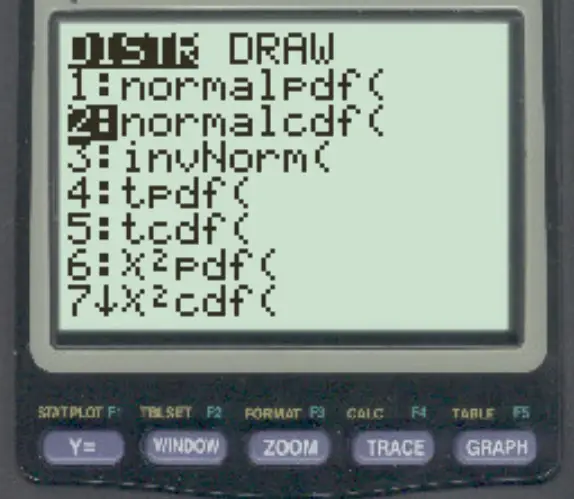
Poniższe przykłady pokazują, jak w praktyce wykorzystać tę funkcję.

Przykład 1: Znajdź prawdopodobieństwo między dwiema wartościami

Rozkład ma średnią 70 i odchylenie standardowe 7. Jeśli wybierzemy losową próbę o wielkości n = 35, znajdź prawdopodobieństwo, że średnia próbki mieści się w przedziale od 68 do 72.

Na TI-84 możemy zastosować następującą składnię:

 normalcdf (68, 72, 70, 7/√ 35 ) 

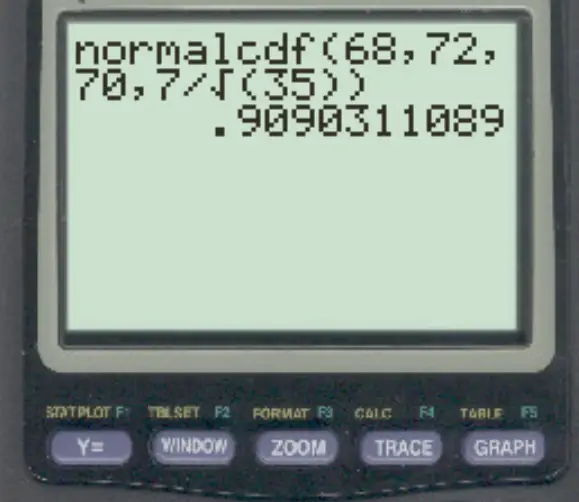
Prawdopodobieństwo, że średnia próbki mieści się w przedziale od 68 do 72, wynosi 0,909 .

Przykład 2: Znajdowanie prawdopodobieństwa większego niż wartość

Rozkład ma średnią 50 i odchylenie standardowe 4. Jeśli wybierzemy losową próbę o wielkości n = 30, znajdź prawdopodobieństwo, że średnia próbki jest większa niż 48.

Na TI-84 możemy zastosować następującą składnię:

 normalcdf (48, E99, 50, 4/√ 30 )

Uwaga: Dostęp do symbolu „E” można uzyskać, naciskając 2 , a następnie naciskając przycisk , .

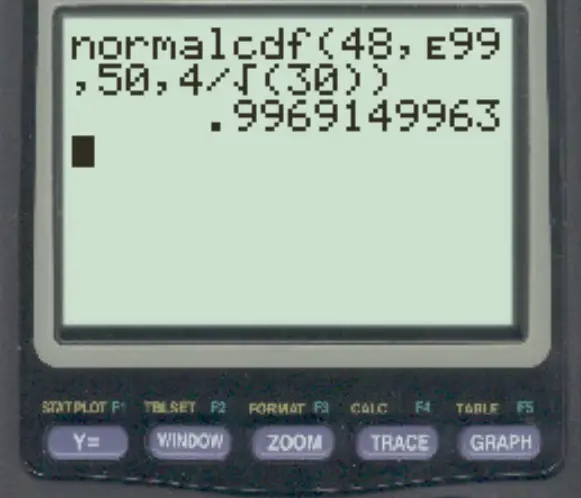
Prawdopodobieństwo, że średnia próbki jest większa niż 48, wynosi 0,9969 .

Przykład 3: Znajdowanie prawdopodobieństwa mniejszego niż wartość

Rozkład ma średnią 20 i odchylenie standardowe 3. Jeśli wybierzemy losową próbę o wielkości n = 40, znajdź prawdopodobieństwo, że średnia próbki jest mniejsza niż 19.

Na TI-84 możemy zastosować następującą składnię:

 normalcdf (-E99, 19, 20, 3/√ 40 ) 

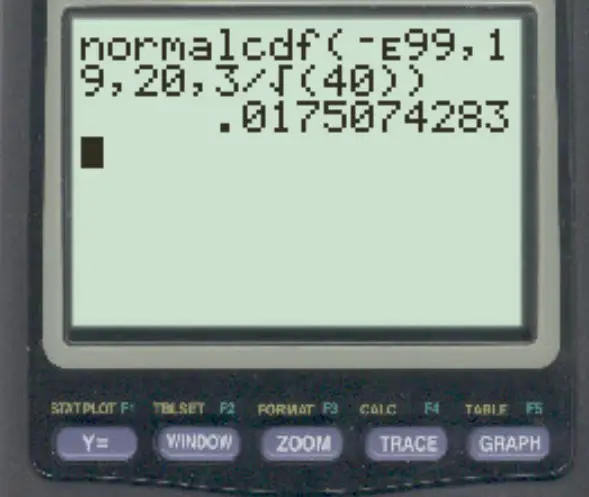
Prawdopodobieństwo, że średnia próbki jest mniejsza niż 19, wynosi 0,0175 .

Dodatkowe zasoby

Wprowadzenie do centralnego twierdzenia granicznego
Kalkulator centralnego twierdzenia granicznego
Jak zastosować centralne twierdzenie graniczne w programie Excel
Centralne twierdzenie graniczne: cztery warunki do spełnienia