Jak zastosować centralne twierdzenie graniczne w r (z przykładami)

Centralne twierdzenie graniczne stwierdza, że rozkład próbkowania średniej próbki jest w przybliżeniu normalny, jeśli wielkość próby jest wystarczająco duża, nawet jeśli rozkład populacji nie jest normalny.

Centralne twierdzenie graniczne stwierdza również, że rozkład próbkowania będzie miał następujące właściwości:

1. Średnia rozkładu próby będzie równa średniej rozkładu populacji:

x = μ

2. Odchylenie standardowe rozkładu próby będzie równe odchyleniu standardowemu rozkładu populacji podzielonemu przez liczebność próby:

s = σ /n

Poniższy przykład pokazuje, jak zastosować centralne twierdzenie graniczne w R.

Przykład: zastosowanie centralnego twierdzenia granicznego w R

Załóżmy, że szerokość skorupy żółwia ma równomierny rozkład o minimalnej szerokości 2 cali i maksymalnej szerokości 6 cali.

Oznacza to, że jeśli wybierzemy losowo żółwia i zmierzymy szerokość jego skorupy, prawdopodobnie będzie on miał również od 2 do 6 cali szerokości .

Poniższy kod pokazuje, jak utworzyć zbiór danych w R zawierający pomiary szerokości pancerza 1000 żółwi, równomiernie rozłożone pomiędzy 2 a 6 cali:

 #make this example reproducible
set. seeds (0)

#create random variable with sample size of 1000 that is uniformly distributed
data <- runif(n=1000, min=2, max=6)

#create histogram to visualize distribution of turtle shell widths
hist(data, col=' steelblue ', main=' Histogram of Turtle Shell Widths ')

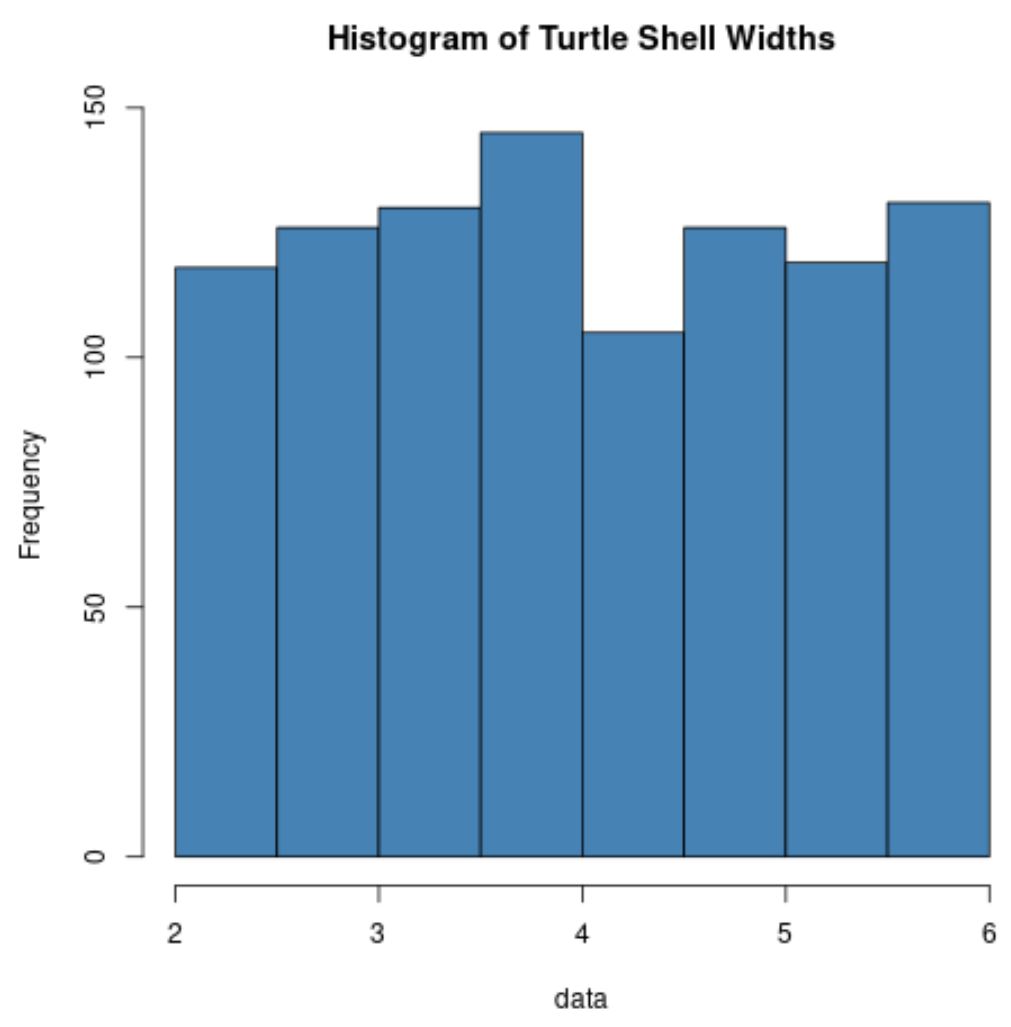
Należy zauważyć, że rozkład szerokości skorupy żółwia zwykle nie jest w ogóle rozłożony.

Teraz wyobraź sobie, że pobieramy losowe próbki 5 żółwi z tej populacji i w kółko mierzymy średnią z próbki.

Poniższy kod pokazuje, jak wykonać ten proces w języku R i utworzyć histogram w celu wizualizacji rozkładu średnich z próbki:

 #create empty vector to hold sample means
sample5 <- c()

#take 1,000 random samples of size n=5
n = 1000
for (i in 1:n){
sample5[i] = mean(sample(data, 5, replace= TRUE ))
}

#calculate mean and standard deviation of sample means
mean(sample5)

[1] 4.008103

sd(sample5)

[1] 0.5171083 

#create histogram to visualize sampling distribution of sample means
hist(sample5, col = ' steelblue ', xlab=' Turtle Shell Width ', main=' Sample size = 5 ') 

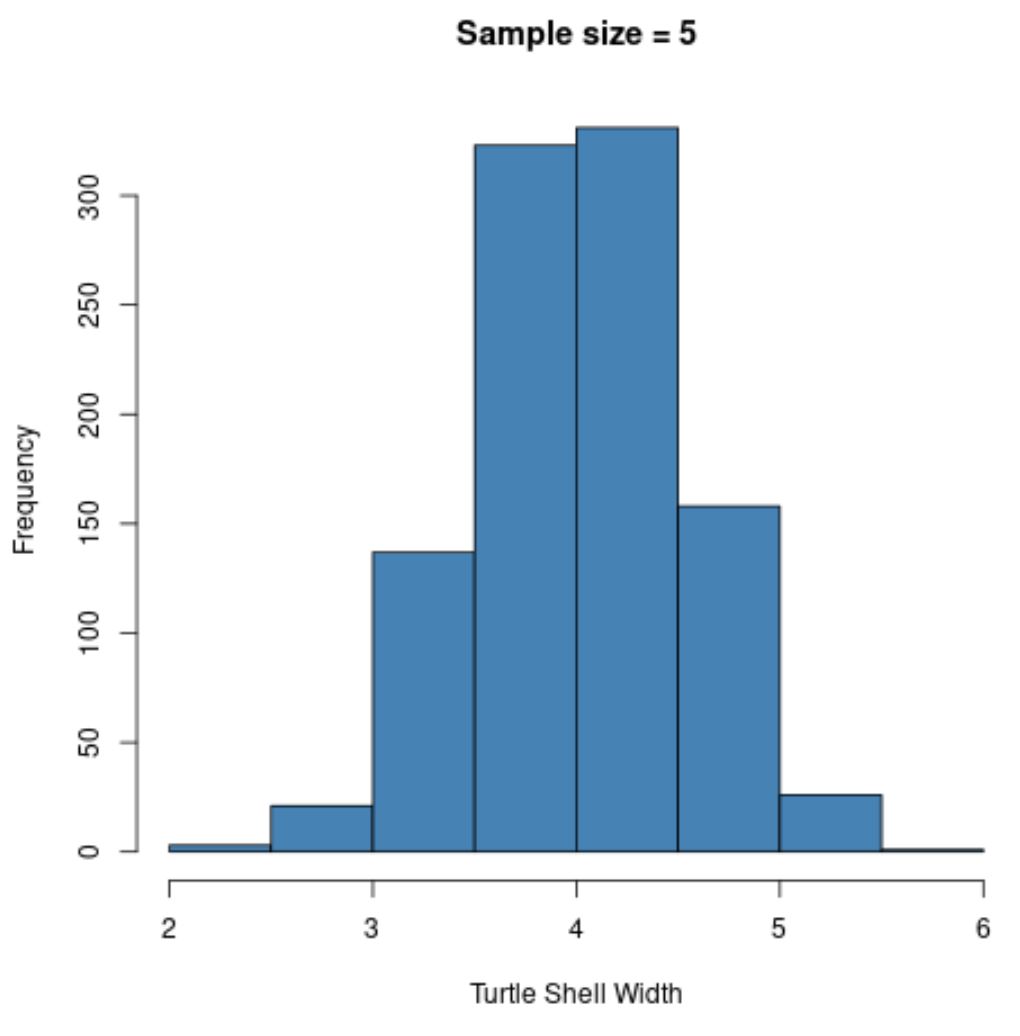
Należy zauważyć, że rozkład próbkowania średnich próbek wydaje się mieć rozkład normalny, nawet jeśli rozkład, z którego pochodzą próbki, nie miał rozkładu normalnego.

Należy również zwrócić uwagę na średnią próbki i odchylenie standardowe próbki dla tego rozkładu próbkowania:

• x̄ : 4,008
• s : 0,517

Załóżmy teraz, że zwiększymy wielkość próbki z n=5 do n=30 i odtworzymy histogram średnich z próbki:

 #create empty vector to hold sample means
sample30 <- c()

#take 1,000 random samples of size n=30
n = 1000
for (i in 1:n){
sample30[i] = mean(sample(data, 30, replace= TRUE ))
}

#calculate mean and standard deviation of sample means
mean(sample30)

[1] 4.000472

sd(sample30)

[1] 0.2003791

#create histogram to visualize sampling distribution of sample means
hist(sample30, col = ' steelblue ', xlab=' Turtle Shell Width ', main=' Sample size = 30 ') 

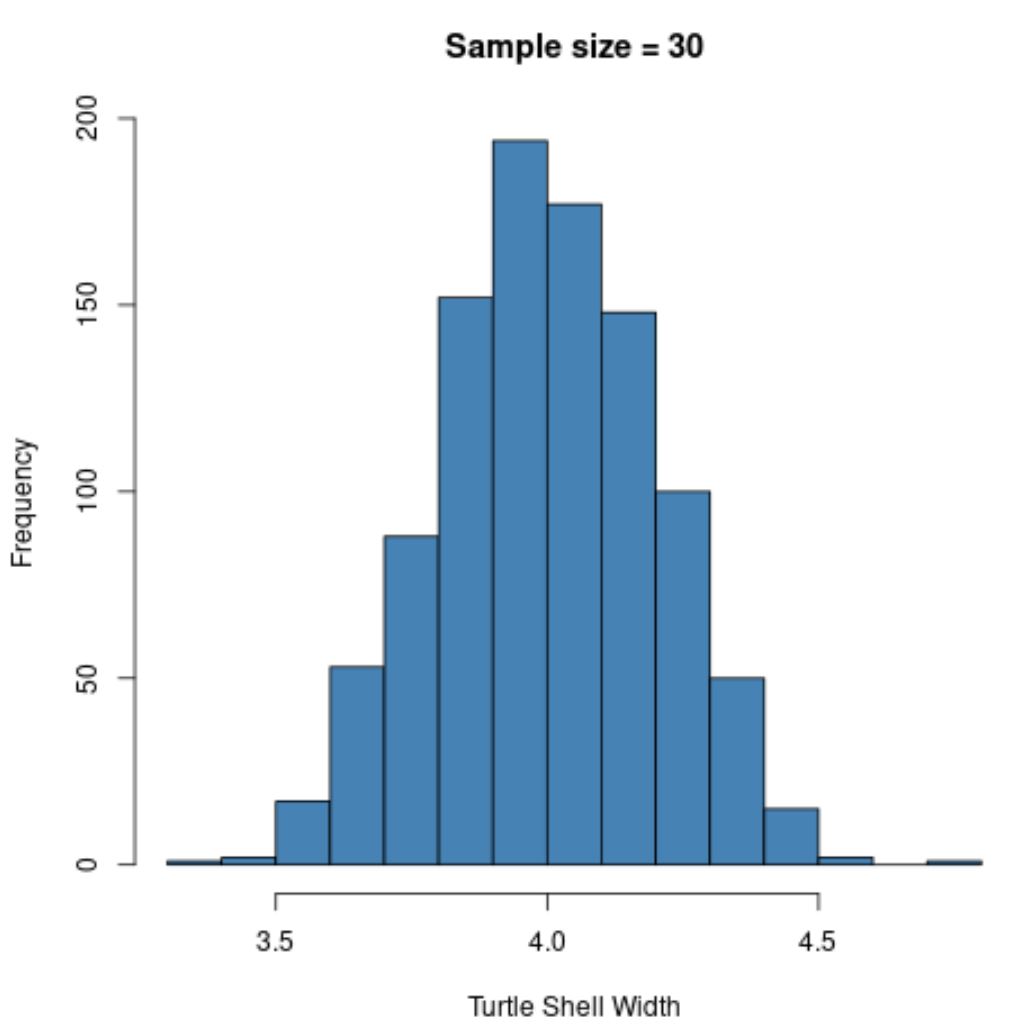
Rozkład próbkowania ma ponownie rozkład normalny , ale odchylenie standardowe próbki jest jeszcze mniejsze:

• s : 0,200

Dzieje się tak, ponieważ użyliśmy większej próby (n=30) w porównaniu z poprzednim przykładem (n=5), więc odchylenie standardowe średnich z próby jest jeszcze mniejsze.

Jeśli będziemy nadal korzystać z coraz większych próbek, odkryjemy, że odchylenie standardowe próbki staje się coraz mniejsze.

To ilustruje centralne twierdzenie graniczne w praktyce.

Dodatkowe zasoby

Poniższe zasoby dostarczają dodatkowych informacji na temat centralnego twierdzenia granicznego:

Wprowadzenie do centralnego twierdzenia granicznego
Kalkulator centralnego twierdzenia granicznego
5 przykładów zastosowania centralnego twierdzenia granicznego w życiu codziennym