Co oznacza wysoka wartość f w anova?
Jednoczynnikową analizę ANOVA stosuje się do określenia, czy średnie trzech lub większej liczby niezależnych grup są równe.
Jednoczynnikowa ANOVA wykorzystuje następujące hipotezy zerowe i alternatywne:
- H 0 : Wszystkie średnie grupowe są równe.
- H A : Przynajmniej jedna średnia grupowa różni się od pozostałych.
Za każdym razem, gdy przeprowadzasz jednokierunkową analizę ANOVA, otrzymasz tabelę podsumowującą, która wygląda następująco:
| Źródło | Suma kwadratów (SS) | zm | Średnie kwadraty (MS) | F | Wartość P |
|---|---|---|---|---|---|
| Leczenie | 192.2 | 2 | 96.1 | 2358 | 0,1138 |
| Błąd | 1100,6 | 27 | 40,8 | ||
| Całkowity | 1292,8 | 29 |
Wartość F w tabeli oblicza się w następujący sposób:
- Wartość F = przetwarzanie średnich kwadratów / błąd średnich kwadratów
Innym sposobem napisania tego jest:
- Wartość F = różnica pomiędzy średnimi próbkami/zmienność w obrębie próbek
Jeśli różnica między średnimi próbek jest duża w porównaniu ze zmiennością w obrębie każdej próbki, wówczas wartość F będzie duża.
Na przykład wartość F w powyższej tabeli oblicza się w następujący sposób:
- Wartość F = 96,1 / 40,8 = 2,358
Aby znaleźć wartość p odpowiadającą tej wartości F, możemy użyć kalkulatora rozkładu F ze stopniami swobody w liczniku = df Leczenie i stopniami swobody w mianowniku = df Błąd.
Na przykład wartość p odpowiadająca wartości F wynoszącej 2,358, licznik df = 2 i mianownik df = 27 wynoszą 0,1138 .
Ponieważ ta wartość p jest nie mniejsza niż α = 0,05, nie możemy odrzucić hipotezy zerowej. Oznacza to, że nie ma statystycznie istotnej różnicy pomiędzy średnimi trzech grup.
Zobacz wartość F analizy ANOVA
Aby uzyskać intuicyjne zrozumienie wartości F w tabeli ANOVA, rozważ następujący przykład.
Załóżmy, że chcemy przeprowadzić jednoczynnikową analizę ANOVA, aby ustalić, czy trzy różne techniki uczenia się dają różne średnie wyniki egzaminu. Poniższa tabela przedstawia wyniki egzaminu 10 uczniów, którzy zastosowali każdą technikę:
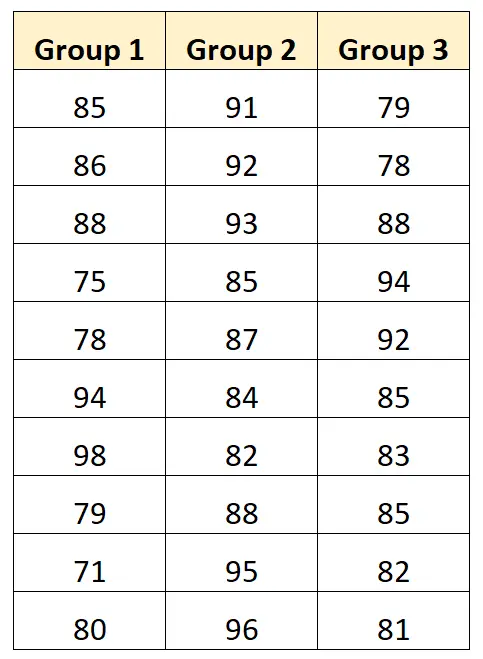
Aby zwizualizować wyniki egzaminu w podziale na grupy, możemy utworzyć następujący wykres:
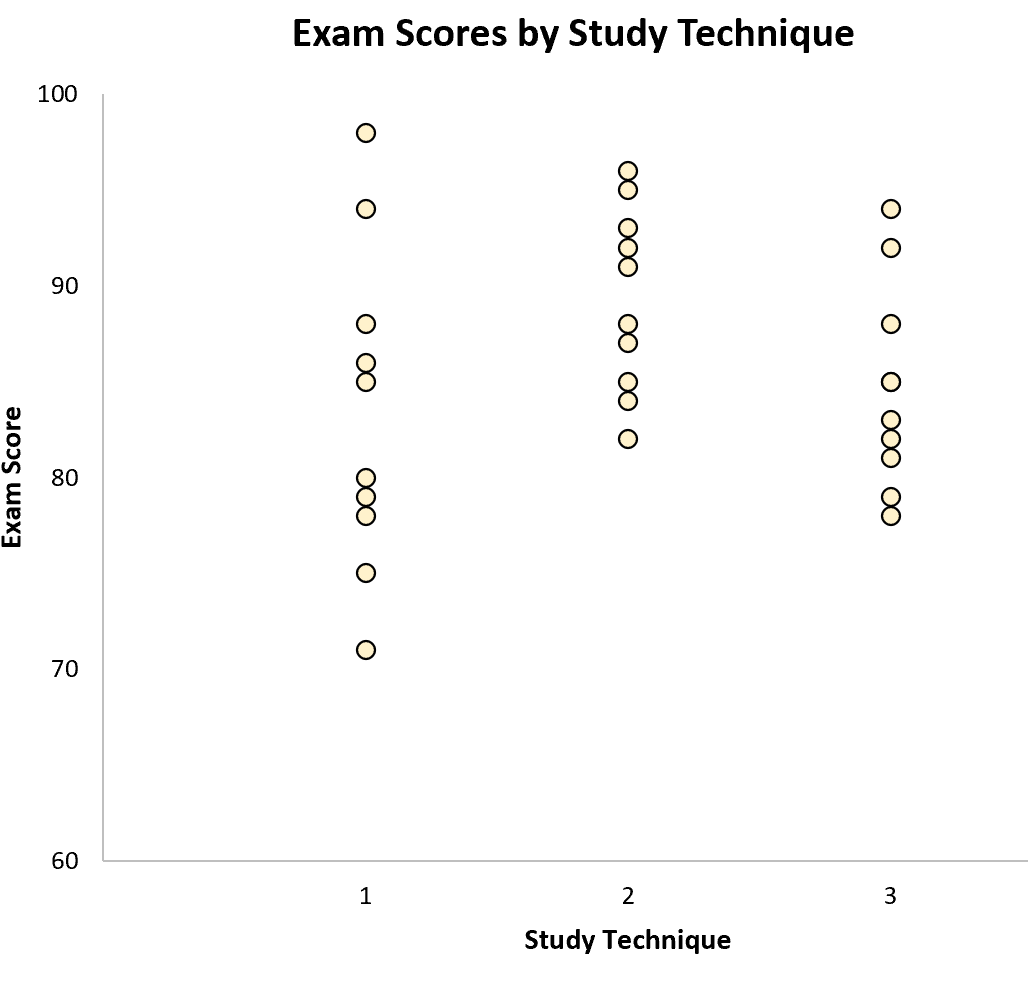
Zmienność w obrębie próbek jest reprezentowana przez rozkład wartości w obrębie każdej pojedynczej próbki:
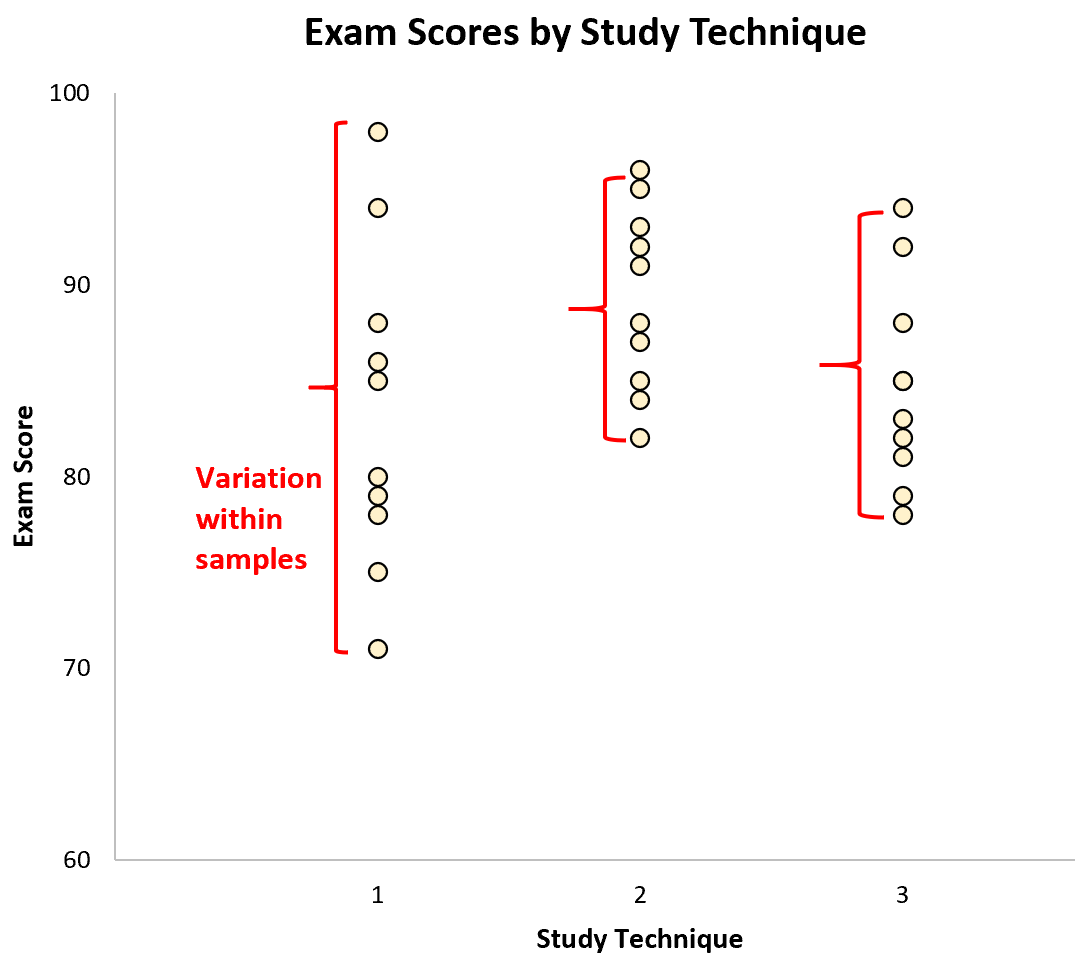
Różnice między próbkami są reprezentowane przez różnice między średnimi próbek:
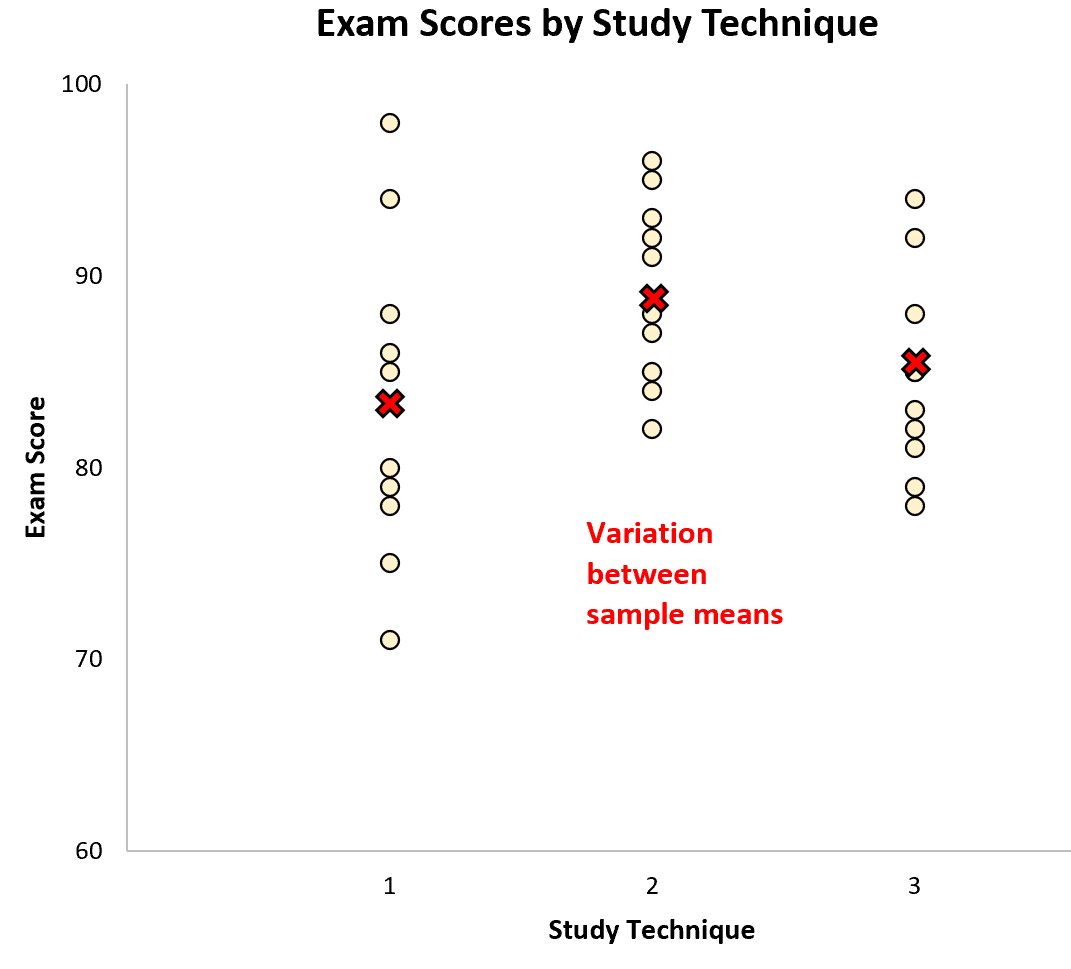
Wykonując jednoczynnikową analizę ANOVA dla tego zbioru danych, stwierdzamy, że wartość F wynosi 2,358 , a odpowiadająca wartość p wynosi 0,1138 .
Ponieważ ta wartość p jest nie mniejsza niż 0,05, nie możemy odrzucić hipotezy zerowej. Oznacza to, że nie mamy wystarczających dowodów, aby stwierdzić, że zastosowana technika badania powoduje statystycznie istotne różnice w średnich wynikach egzaminów.
Innymi słowy, mówi nam to, że różnica między średnimi z próbki nie jest wystarczająco duża w stosunku do zmienności w obrębie próbek, aby odrzucić hipotezę zerową.
Wniosek
Oto krótkie podsumowanie głównych punktów tego artykułu:
- Wartość F w ANOVA oblicza się jako: zmienność pomiędzy średnimi próbek / zmienność w obrębie próbek.
- Im wyższa wartość F w ANOVA, tym większa zmienność między średnimi próbek w stosunku do zmienności w obrębie próbek.
- Im wyższa wartość F, tym niższa odpowiadająca jej wartość p.
- Jeżeli wartość p jest poniżej pewnego progu (np. α = 0,05), możemy odrzucić hipotezę zerową analizy ANOVA i stwierdzić, że istnieje statystycznie istotna różnica pomiędzy średnimi grupowymi.
Dodatkowe zasoby
Jak wykonać jednokierunkową ANOVA w programie Excel
Jak ręcznie wykonać jednokierunkową ANOVA
Jednokierunkowy kalkulator ANOVA