Co to znaczy, że statystyka jest odporna?

Mówi się, że statystyka jest odporna , jeśli nie jest wrażliwa na wartości ekstremalne.

Oto dwa przykłady odpornych statystyk:

• Mediana
• Rozstęp międzykwartylowy

Oto przykłady statystyk, które się nie sprawdzają :

• Średnia
• Odchylenie standardowe
• Czysty

Poniższy przykład ilustruje różnicę między statystykami odpornymi i nieodpornymi.

Przykład: statystyki odporne i nieodporne

Załóżmy, że mamy następujący zbiór danych:

Zbiór danych: 2, 5, 6, 7, 8, 13, 15, 18, 22, 24, 29

Za pomocą kalkulatora lub oprogramowania statystycznego możemy obliczyć wartość następujących statystyk holdingowych dla tego zbioru danych:

• Mediana: 13
• Rozstęp międzykwartylowy: 13,5

Możemy również obliczyć wartość następujących nieodpornych statystyk dla tego zbioru danych:

• Średnia: 13,54
• Odchylenie standardowe: 8,82
• Zasięg: 27

Rozważmy teraz, czy do tego zbioru danych dodano skrajną wartość odstającą:

Zbiór danych: 2, 5, 6, 7, 8, 13, 15, 18, 22, 24, 29, 450

Możemy ponownie obliczyć wartość następujących odpornych statystyk dla tego zbioru danych:

• Mediana: 14
• Rozstęp międzykwartylowy: 15,75

Możemy również obliczyć wartość następujących nieodpornych statystyk dla tego zbioru danych:

• Średnia: 49,92
• Odchylenie standardowe: 126,27
• Zasięg: 448

Zwróć uwagę, jak bardzo zmieniły się statystyki braku oporu, po prostu dodając ekstremalną wartość do zbioru danych:

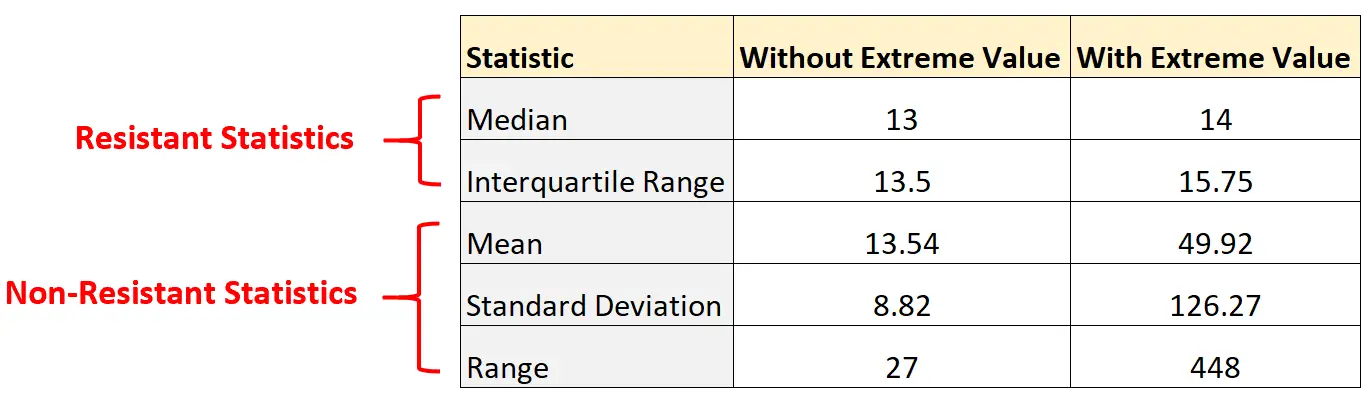
I odwrotnie, statystyki bojowników ruchu oporu prawie się nie zmieniły. Mediana i rozstęp międzykwartylowy zmieniły się jedynie nieznacznie.

Kiedy używać odpornych statystyk

Najczęściej używanymi statystykami do pomiaru środka i rozproszenia wartości w zbiorze danych są odpowiednio średnia i odchylenie standardowe.

Niestety obie te statystyki są wrażliwe na wartości ekstremalne. Jeśli zatem w zbiorze danych występują wartości odstające, średnia i odchylenie standardowe nie będą dokładnie opisywać rozkładu wartości w zbiorze danych.

Zamiast tego zaleca się użycie mediany i rozstępu międzykwartylowego do pomiaru środka i rozproszenia wartości w zbiorze danych, jeśli występują wartości odstające, ponieważ obie te statystyki są solidne .

Dodatkowe zasoby

Jak wartości odstające wpływają na średnią?
Kiedy stosować średnią a kiedy medianę
Kiedy stosować rozstęp międzykwartylowy a odchylenie standardowe