Przykładowa proporcja

W tym artykule wyjaśniono, czym jest proporcja próby w statystyce. W ten sposób dowiesz się, jak obliczyć proporcję próby, jakie jest rozwiązane ćwiczenie, a także jaka jest różnica między proporcją próby a proporcją populacji.

Jaka jest proporcja próbki?

Proporcja próbki to stosunek pomyślnych przypadków w próbie do jej wielkości. Dlatego, aby obliczyć proporcję próby, liczbę sukcesów w próbie należy podzielić przez całkowitą liczbę danych.

Symbol proporcji próbki to

.

W statystyce, przeprowadzając badanie, nie wszystkie dane dotyczące populacji są zwykle znane, dlatego zwykle przeprowadza się badanie na reprezentatywnej próbie, a następnie wyciągnięte wnioski ekstrapoluje się na całą populację. populacja. Zatem proporcja próby służy do oszacowania odsetka całej populacji. Poniżej zobaczymy, jak to się robi.

Przykład wzoru proporcji

Proporcja próby jest równa liczbie pomyślnych przypadków w próbie podzielonej przez wielkość próby. Zatem wzór na obliczenie proporcji próbki jest następujący:

Złoto:

• 

  jest proporcją próbki.

• 

  to liczba pomyślnych przypadków w próbie.

• 

  to całkowita liczba elementów danych w próbie.

Przykładowy przykład obliczenia proporcji

Po zapoznaniu się z definicją proporcji próbki i jej wzorem, w tej sekcji rozwiążemy prosty przykład, abyś mógł zobaczyć, jak obliczana jest proporcja próbki.

• Firma produkuje zabawkę i kupuje jedną z jej części od innej firmy zewnętrznej. Jednak w kupowanych przez niego partiach pojawiają się części wadliwe, dlatego postanawia przeprowadzić badanie statystyczne, aby dowiedzieć się, jaka jest proporcja części w dobrym stanie i proporcja wad. Zamawiasz więc próbkę 1000 sztuk i znajdujesz 138 wadliwych części. Jaki jest udział części w dobrym stanie w próbce? A jaka jest proporcja wadliwych części w próbce?

Liczba nieuszkodzonych części w próbce wynosi 1000 minus liczba wadliwych części:

Aby znaleźć proporcję próbki, stosujemy wzór, który widzieliśmy powyżej:

Udział próbki części w dobrym stanie wynosi zatem 86,2%.

Z drugiej strony proporcja części wadliwych jest równa jeden minus proporcja części dobrych:

Udział próbek wadliwych części wynosi zatem 13,8%.

Proporcja próby i proporcja populacji

Proporcja populacji to odsetek populacji statystycznej. Oznacza to, że proporcja populacji to stosunek przypadków sukcesu badanej populacji do wszystkich elementów wchodzących w skład tej populacji.

Dlatego różnica między proporcją narodową a proporcją populacji polega na tym, że proporcja narodowa to proporcja przypadków większości, w zamian proporcja populacji odnosi się do proporcji przypadków zdarzeń dotyczących wszystkich elementów Populacja.

Aby odróżnić odsetek próby od odsetka populacji, są one oznaczone różnymi symbolami. Symbol proporcji próbki to

, podczas gdy symbolem proporcji populacji jest

.

Ogólnie rzecz biorąc, nie można dokładnie określić proporcji populacji, ponieważ nie wszystkie wartości populacji są zwykle znane. Zamiast tego wartość odsetka ludności szacuje się zwykle przy użyciu przedziału ufności o następującym wzorze:

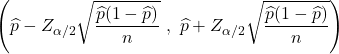
Aby zobaczyć jak szacowana jest proporcja populacji, kliknij poniższy link:

Próbkowanie rozkładu proporcji

Na koniec zobaczymy, na czym polega próbkowanie rozkładu proporcji, ponieważ jest to pojęcie statystyczne związane z proporcją próbkowania.

Zacznijmy od zdefiniowania, czym jest rozkład próbkowania. Rozkład próby to rozkład będący wynikiem uwzględnienia wszystkich możliwych próbek z populacji statystycznej.

Zatem rozkład proporcji próbkowania to rozkład wynikający z obliczenia proporcji każdej możliwej próbki z populacji. Oznacza to, że jeśli przeanalizujemy wszystkie możliwe próbki z populacji i obliczymy proporcję każdej z próbek, obliczony zbiór wartości będzie rozkładem próbkowania proporcji próbek.