Jak obliczyć korelację częściową w programie excel

W statystyce często używamy współczynnika korelacji Pearsona do pomiaru liniowej zależności między dwiema zmiennymi. Czasami jednak chcemy zrozumieć związek między dwiema zmiennymi , kontrolując trzecią zmienną .

Załóżmy na przykład, że chcemy zmierzyć związek między liczbą godzin nauki studenta a oceną z egzaminu końcowego, kontrolując jednocześnie aktualną ocenę studenta z zajęć. W tym przypadku moglibyśmy zastosować częściową korelację do pomiaru związku między przepracowanymi godzinami a oceną końcową z egzaminu.

W tym samouczku wyjaśniono, jak obliczyć częściową korelację w programie Excel.

Przykład: korelacja częściowa w Excelu

Załóżmy, że mamy zbiór danych, który wyświetla następujące informacje dla 10 uczniów:

• Aktualna ocena w klasie
• Godziny spędzone na nauce do egzaminu końcowego
• Końcowy wynik egzaminu

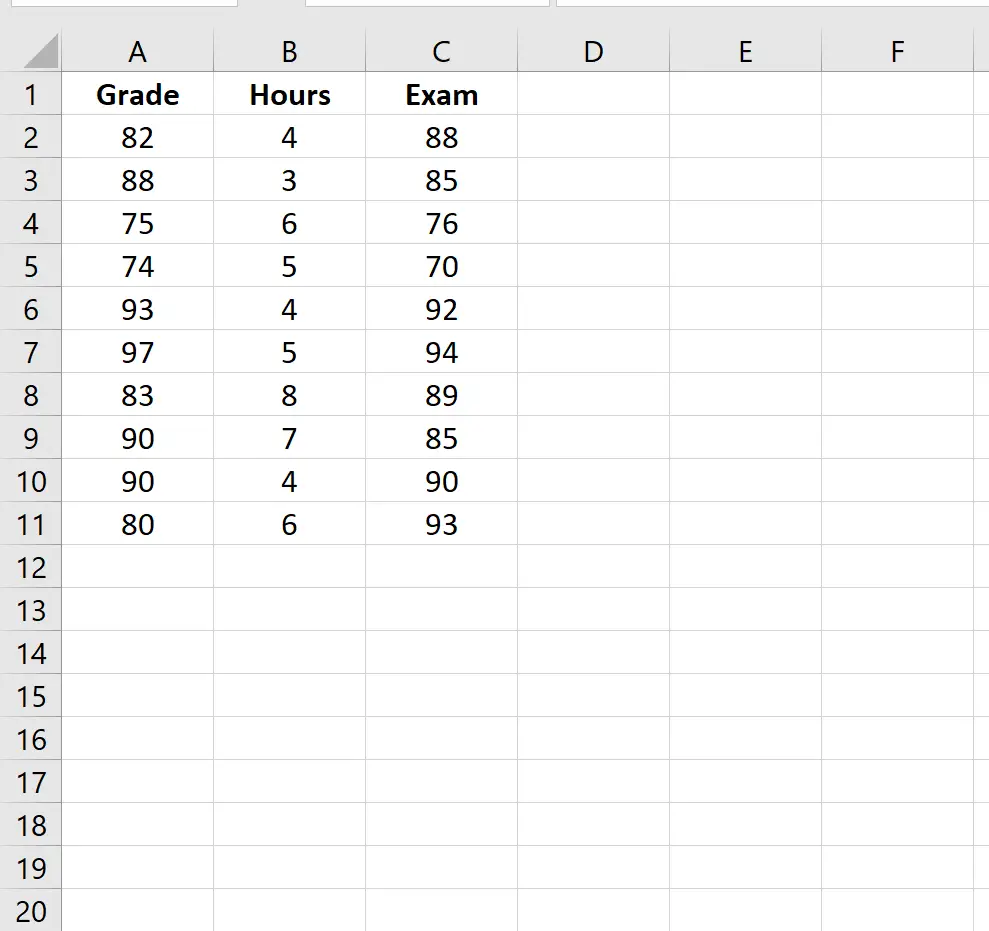
Wykonaj poniższe kroki, aby znaleźć częściową korelację między przestudiowanymi godzinami a oceną z egzaminu, kontrolując jednocześnie aktualną ocenę.

Krok 1: Oblicz korelację każdej pary.

Najpierw obliczymy korelację pomiędzy każdą kombinacją par zmiennych:

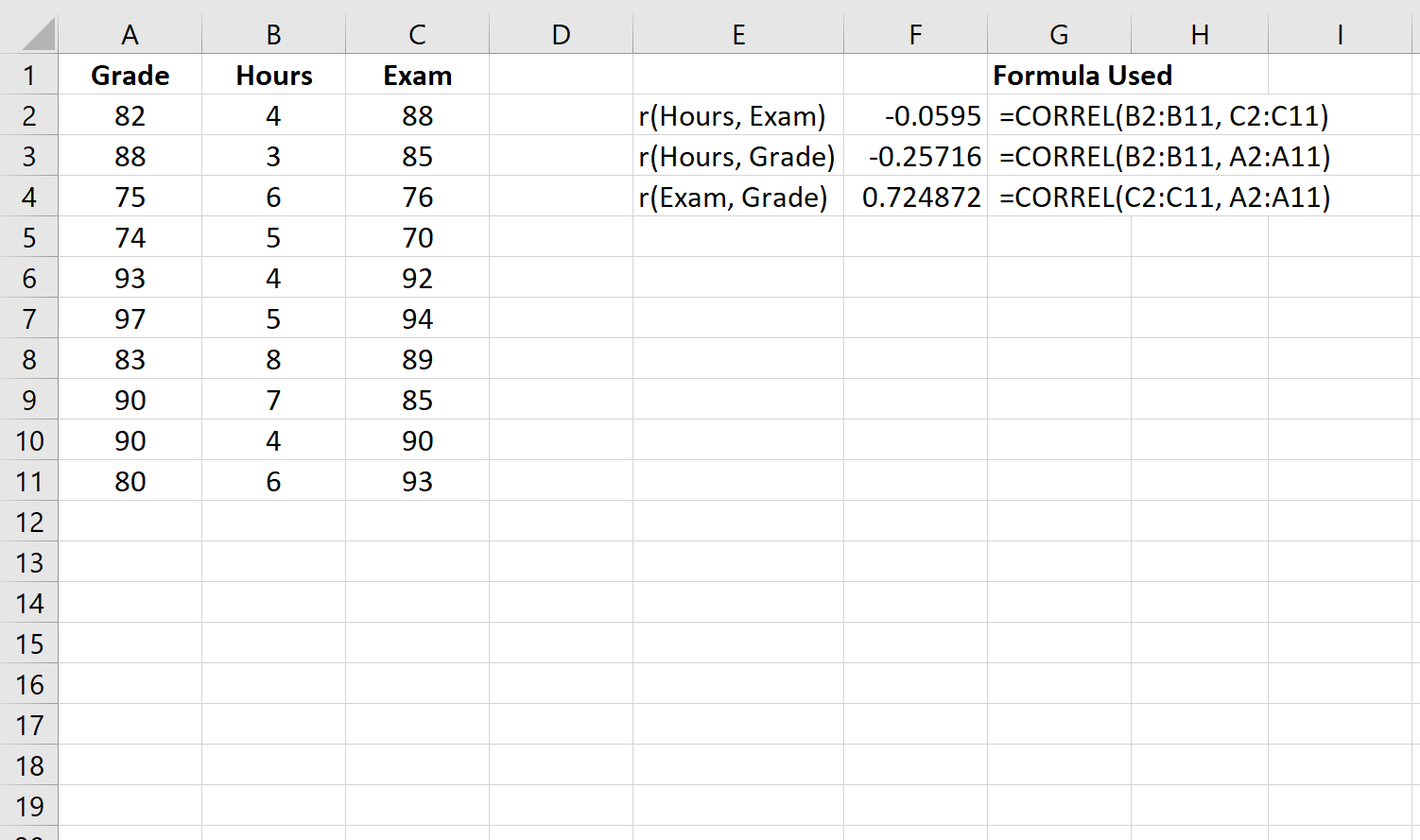
Krok 2: Oblicz częściową korelację między godzinami a wynikiem egzaminu.

Wzór na obliczenie częściowej korelacji pomiędzy zmienną A i zmienną B przy uwzględnieniu zmiennej C jest następujący:

Częściowa korelacja = (r _A,B – r _A,C *r _B,C ) / √((1-r ² _A,B )(1-r ² _B,C ))

Poniższy zrzut ekranu pokazuje, jak użyć tej formuły do obliczenia częściowej korelacji między godzinami a oceną z egzaminu, kontrolując bieżącą ocenę:

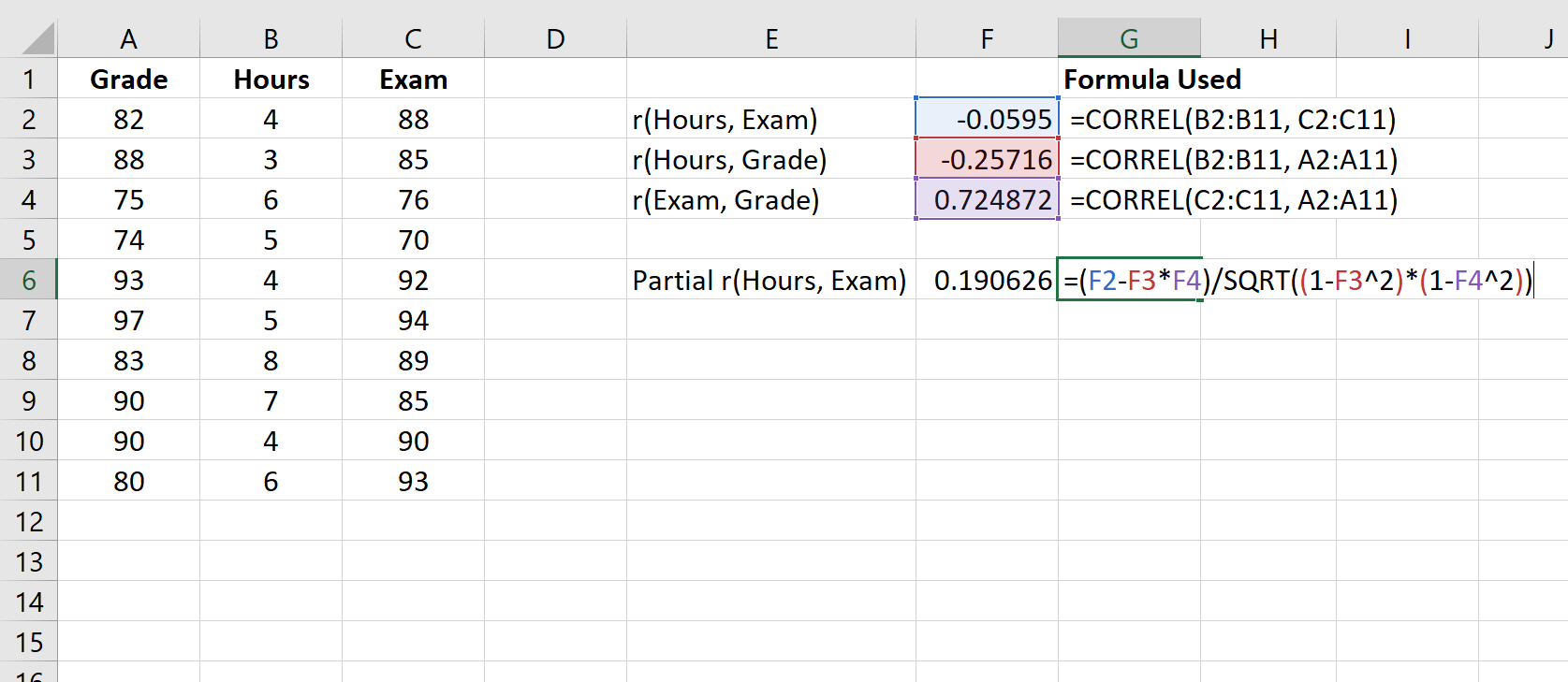
Częściowa korelacja wynosi 0,190626 . Aby określić, czy ta korelacja jest istotna statystycznie, możemy znaleźć odpowiednią wartość p.

Krok 3: Oblicz wartość p korelacji częściowej.

Statystykę testu t można obliczyć w następujący sposób:

t = r√(n-3) / √(1-r ² )

Poniższy zrzut ekranu pokazuje, jak używać tej formuły do obliczenia statystyki testowej i odpowiadającej jej wartości p:

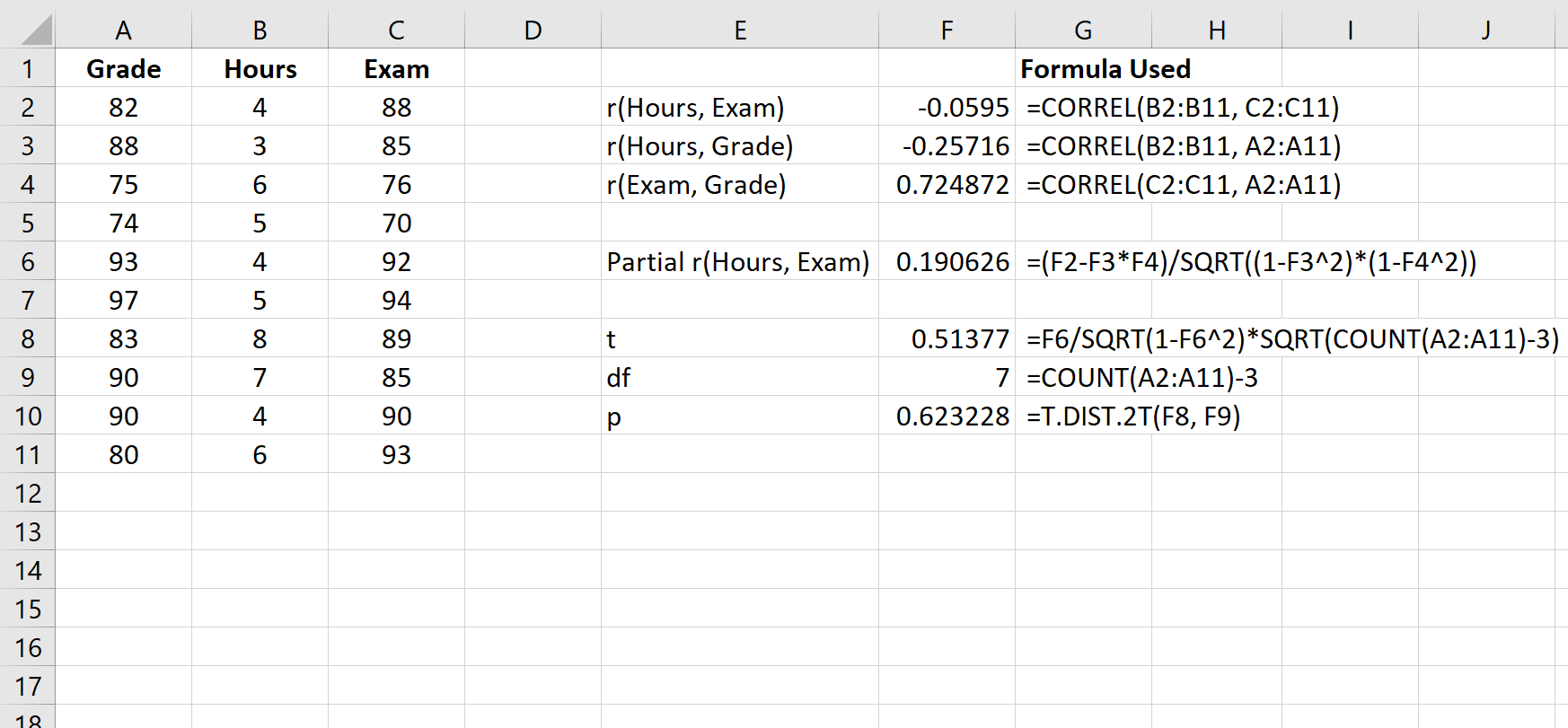
Statystyka testu t wynosi 0,51377 . Całkowita liczba stopni swobody wynosi n-3 = 10-3 = 7 . Odpowiednia wartość p wynosi 0,623228 . Ponieważ wartość ta jest nie mniejsza niż 0,05, oznacza to, że częściowa korelacja pomiędzy godzinami a wynikami egzaminu nie jest istotna statystycznie.