Częściowe najmniejsze kwadraty w r (krok po kroku)

Jednym z najczęstszych problemów, jakie można napotkać w uczeniu maszynowym, jest wieloliniowość . Dzieje się tak, gdy dwie lub więcej zmiennych predykcyjnych w zbiorze danych jest silnie skorelowanych.

Kiedy tak się stanie, model może dobrze dopasować się do zbioru danych uczących, ale może działać słabo na nowym zbiorze danych, którego nigdy nie widział, ponieważ nadmiernie pasuje do zbioru uczącego. zestaw treningowy.

Jednym ze sposobów obejścia tego problemu jest zastosowanie metody zwanej cząstkowymi najmniejszymi kwadratami , która działa w następujący sposób:

• Standaryzacja zmiennych predykcyjnych i odpowiedzi.
• Oblicz M kombinacji liniowych (zwanych „składnikami PLS”) p oryginalnych zmiennych predykcyjnych, które wyjaśniają znaczną ilość zmian zarówno w zmiennej odpowiedzi, jak i zmiennych predykcyjnych.
• Użyj metody najmniejszych kwadratów, aby dopasować model regresji liniowej, używając komponentów PLS jako predyktorów.
• Użyj k-krotnej walidacji krzyżowej , aby znaleźć optymalną liczbę komponentów PLS do utrzymania w modelu.

Ten samouczek zawiera przykład krok po kroku wykonywania częściowych najmniejszych kwadratów w języku R.

Krok 1: Załaduj niezbędne pakiety

Najłatwiejszym sposobem wykonania częściowych najmniejszych kwadratów w R jest użycie funkcji z pakietu pls .

 #install pls package (if not already installed)
install.packages(" pls ")

load pls package
library(pls)

Krok 2: Dopasuj model częściowych najmniejszych kwadratów

W tym przykładzie użyjemy wbudowanego zbioru danych R o nazwie mtcars , który zawiera dane o różnych typach samochodów:

 #view first six rows of mtcars dataset
head(mtcars)

                   mpg cyl disp hp drat wt qsec vs am gear carb
Mazda RX4 21.0 6 160 110 3.90 2.620 16.46 0 1 4 4
Mazda RX4 Wag 21.0 6 160 110 3.90 2.875 17.02 0 1 4 4
Datsun 710 22.8 4 108 93 3.85 2.320 18.61 1 1 4 1
Hornet 4 Drive 21.4 6 258 110 3.08 3.215 19.44 1 0 3 1
Hornet Sportabout 18.7 8 360 175 3.15 3.440 17.02 0 0 3 2
Valiant 18.1 6 225 105 2.76 3,460 20.22 1 0 3 1

W tym przykładzie dopasujemy model częściowych najmniejszych kwadratów (PLS), wykorzystując hp jako zmienną odpowiedzi i następujące zmienne jako zmienne predykcyjne:

• mpg
• wyświetlacz
• gówno
• waga
• sek

Poniższy kod pokazuje, jak dopasować model PLS do tych danych. Zwróć uwagę na następujące argumenty:

• skala=PRAWDA : Mówi R, że każda ze zmiennych w zbiorze danych powinna zostać przeskalowana tak, aby miała średnią 0 i odchylenie standardowe 1. Dzięki temu żadna zmienna predykcyjna nie będzie miała zbyt dużego wpływu na model, jeśli jest mierzona w różnych jednostkach.
• validation=”CV” : Mówi R, aby użył k-krotnej walidacji krzyżowej do oceny wydajności modelu. Zauważ, że domyślnie używa to k=10 fałd. Należy również pamiętać, że zamiast tego można określić „LOOCV”, aby przeprowadzić weryfikację krzyżową Leave-One-Out .

 #make this example reproducible
set.seed(1)

#fit PCR model
model <- plsr(hp~mpg+disp+drat+wt+qsec, data=mtcars, scale= TRUE , validation=" CV ")

Krok 3: Wybierz liczbę komponentów PLS

Po dopasowaniu modelu musimy określić, ile elementów PLS należy zachować.

Aby to zrobić, po prostu spójrz na średni błąd kwadratowy testu (test RMSE) obliczony za pomocą walidacji krzyżowej k:

 #view summary of model fitting
summary(model)

Data: 
	Y dimension: 32 1
Fit method: kernelpls
Number of components considered: 5

VALIDATION: RMSEP
Cross-validated using 10 random segments.
       (Intercept) 1 comp 2 comps 3 comps 4 comps 5 comps
CV 69.66 40.57 35.48 36.22 36.74 36.67
adjCV 69.66 40.41 35.12 35.80 36.27 36.20

TRAINING: % variance explained
    1 comp 2 comps 3 comps 4 comps 5 comps
X 68.66 89.27 95.82 97.94 100.00
hp 71.84 81.74 82.00 82.02 82.03

W rezultacie znajdują się dwie interesujące tabele:

1. WALIDACJA: RMSEP

Ta tabela przedstawia test RMSE obliczony poprzez k-krotną walidację krzyżową. Możemy zobaczyć co następuje:

• Jeśli w modelu użyjemy tylko pierwotnego składnika, RMSE testu wyniesie 69,66 .
• Jeśli dodamy pierwszy składnik PLS, test RMSE spadnie do 40,57.
• Jeśli dodamy drugi składnik PLS, test RMSE spadnie do 35,48.

Widzimy, że dodanie dodatkowych komponentów PLS faktycznie powoduje wzrost RMSE testu. Wydaje się zatem, że optymalne byłoby zastosowanie w ostatecznym modelu jedynie dwóch komponentów PLS.

2. SZKOLENIE: Wyjaśniono % wariancji

Tabela ta podaje procent wariancji zmiennej odpowiedzi wyjaśnionej przez komponenty PLS. Możemy zobaczyć co następuje:

• Używając tylko pierwszej składowej PLS, możemy wyjaśnić 68,66% zmienności zmiennej odpowiedzi.
• Dodając drugi składnik PLS, możemy wyjaśnić 89,27% zmienności zmiennej odpowiedzi.

Należy zauważyć, że nadal będziemy w stanie wyjaśnić większą wariancję, używając większej liczby komponentów PLS, ale widzimy, że dodanie więcej niż dwóch komponentów PLS w rzeczywistości nie zwiększa znacząco procentu wyjaśnionej wariancji.

Test RMSE (wraz z testem MSE i testem R-kwadrat) możemy również zwizualizować w funkcji liczby składowych PLS za pomocą funkcji validationplot() .

 #visualize cross-validation plots
validationplot(model)
validationplot(model, val.type=" MSEP ")
validationplot(model, val.type=" R2 ") 

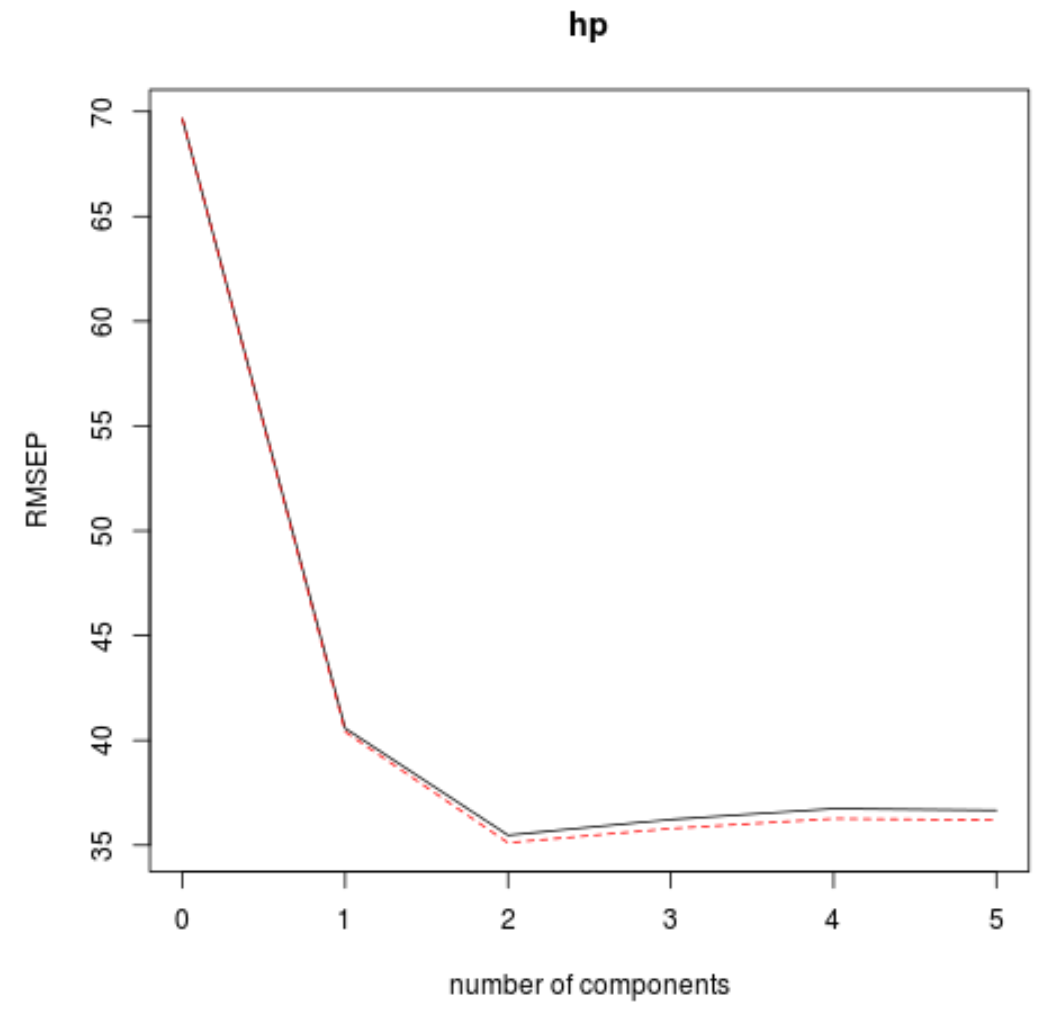
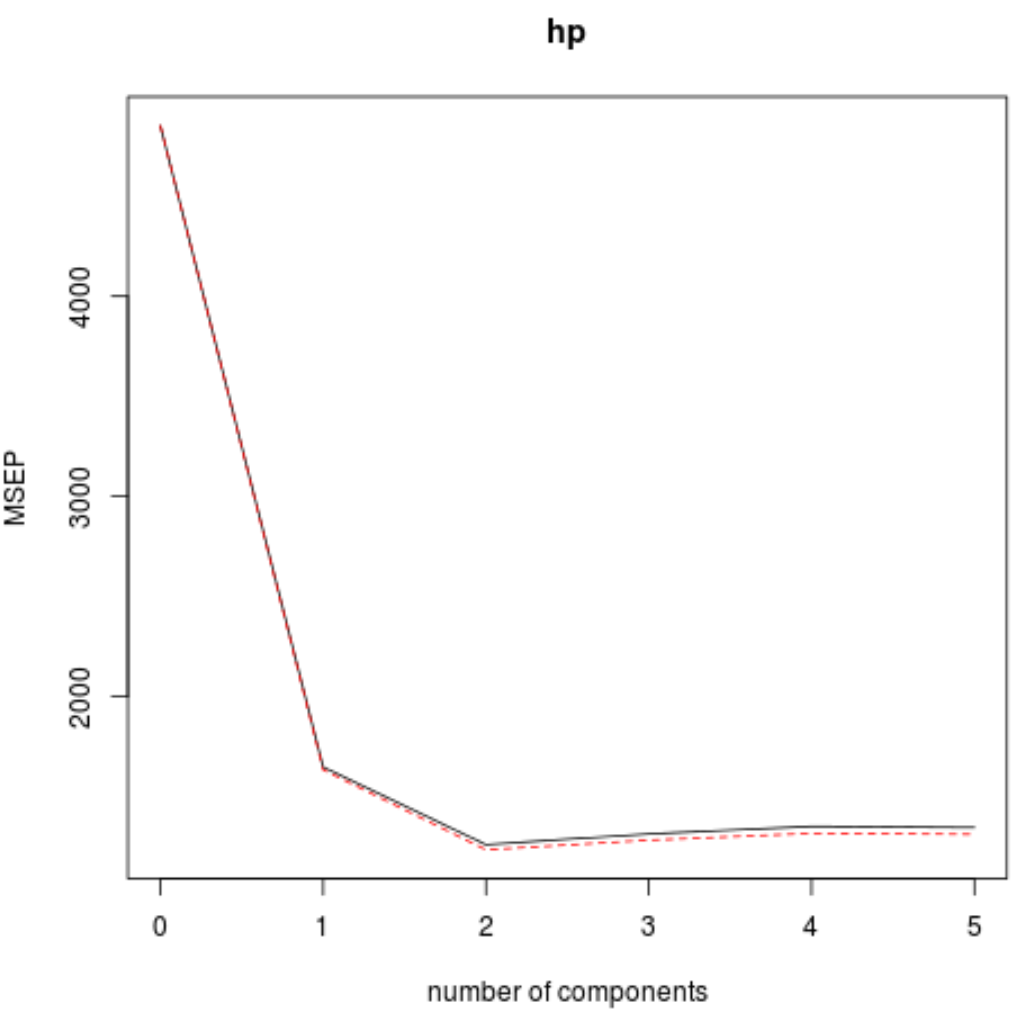
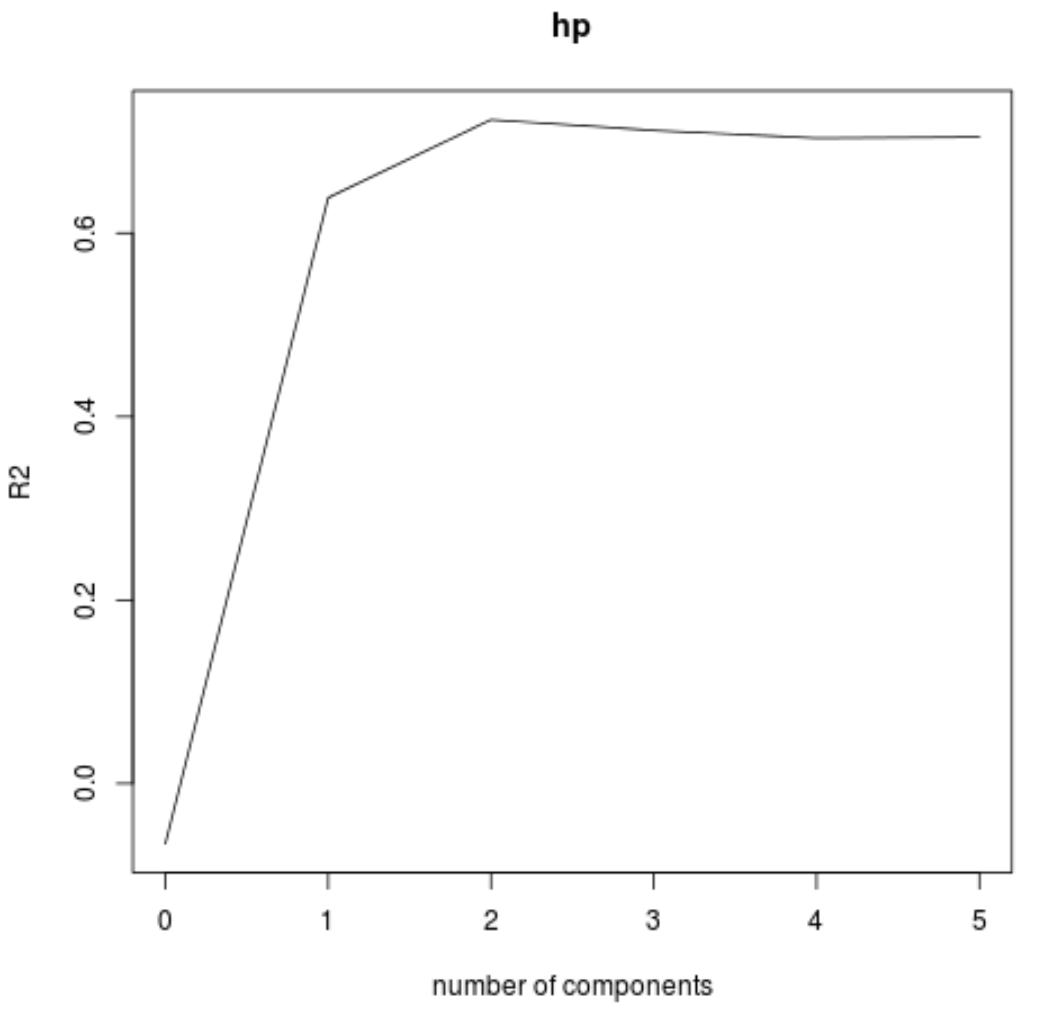
Na każdym wykresie widzimy, że dopasowanie modelu poprawia się po dodaniu dwóch komponentów PLS, ale ma tendencję do pogarszania się, gdy dodajemy więcej komponentów PLS.

Zatem optymalny model obejmuje tylko dwa pierwsze elementy PLS.

Krok 4: Użyj ostatecznego modelu do przewidywania

Możemy wykorzystać ostateczny model z dwoma komponentami PLS do przewidywania nowych obserwacji.

Poniższy kod pokazuje, jak podzielić oryginalny zbiór danych na zbiór uczący i testowy oraz użyć ostatecznego modelu z dwoma komponentami PLS do przewidywania zbioru testowego.

 #define training and testing sets
train <- mtcars[1:25, c("hp", "mpg", "disp", "drat", "wt", "qsec")]
y_test <- mtcars[26: nrow (mtcars), c("hp")]
test <- mtcars[26: nrow (mtcars), c("mpg", "disp", "drat", "wt", "qsec")]
    
#use model to make predictions on a test set
model <- plsr(hp~mpg+disp+drat+wt+qsec, data=train, scale= TRUE , validation=" CV ")
pcr_pred <- predict(model, test, ncomp= 2 )

#calculate RMSE
sqrt ( mean ((pcr_pred - y_test)^2))

[1] 54.89609

Widzimy, że RMSE testu wynosi 54,89609 . Jest to średnie odchylenie pomiędzy przewidywaną wartością KM a obserwowaną wartością KM dla obserwacji zestawu testowego.

Należy zauważyć, że równoważny model regresji głównych składników z dwoma głównymi składnikami dał testowy RMSE wynoszący 56,86549 . Zatem model PLS nieznacznie przewyższał model PCR dla tego zbioru danych.

Pełne wykorzystanie kodu R w tym przykładzie można znaleźć tutaj .