Jak wykonać częściowy test f w programie excel
Częściowy test F służy do określenia, czy istnieje statystycznie istotna różnica między modelem regresji a zagnieżdżoną wersją tego samego modelu.
Model zagnieżdżony to po prostu model zawierający podzbiór zmiennych predykcyjnych w ogólnym modelu regresji.
Załóżmy na przykład, że mamy następujący model regresji z czterema zmiennymi predykcyjnymi:
Y = β 0 + β 1 x 1 + β 2 x 2 + β 3 x 3 + β 4 x 4 + ε
Przykładem modelu zagnieżdżonego może być następujący model z tylko dwoma pierwotnymi zmiennymi predykcyjnymi:
Y = β 0 + β 1 x 1 + β 2 x 2 + ε
Aby ustalić, czy te dwa modele znacząco się różnią, możemy przeprowadzić częściowy test F, który oblicza następującą statystykę testu F:
F = (( Zredukowany RSS – Pełny RSS)/p) / ( Pełny RSS /nk)
Złoto:
- Zredukowany RSS : Pozostała suma kwadratów zredukowanego (tj. „zagnieżdżonego”) modelu.
- RSS pełny : Pozostała suma kwadratów pełnego modelu.
- p: liczba predyktorów usuniętych z pełnego modelu.
- n: całkowita liczba obserwacji w zbiorze danych.
- k: Liczba współczynników (w tym wyraz wolny) w pełnym modelu.
W teście tym wykorzystuje się następujące hipotezy zerowe i alternatywne:
H 0 : Wszystkie współczynniki usunięte z pełnego modelu wynoszą zero.
H A : Co najmniej jeden ze współczynników usuniętych z pełnego modelu jest niezerowy.
Jeśli wartość p odpowiadająca statystyce testu F jest poniżej pewnego poziomu istotności (np. 0,05), to możemy odrzucić hipotezę zerową i stwierdzić, że przynajmniej jeden ze współczynników usuniętych z pełnego modelu jest istotny.
Poniższy przykład pokazuje, jak wykonać częściowy test F w programie Excel.
Przykład: częściowy test F w Excelu
Załóżmy, że w Excelu mamy następujący zestaw danych:
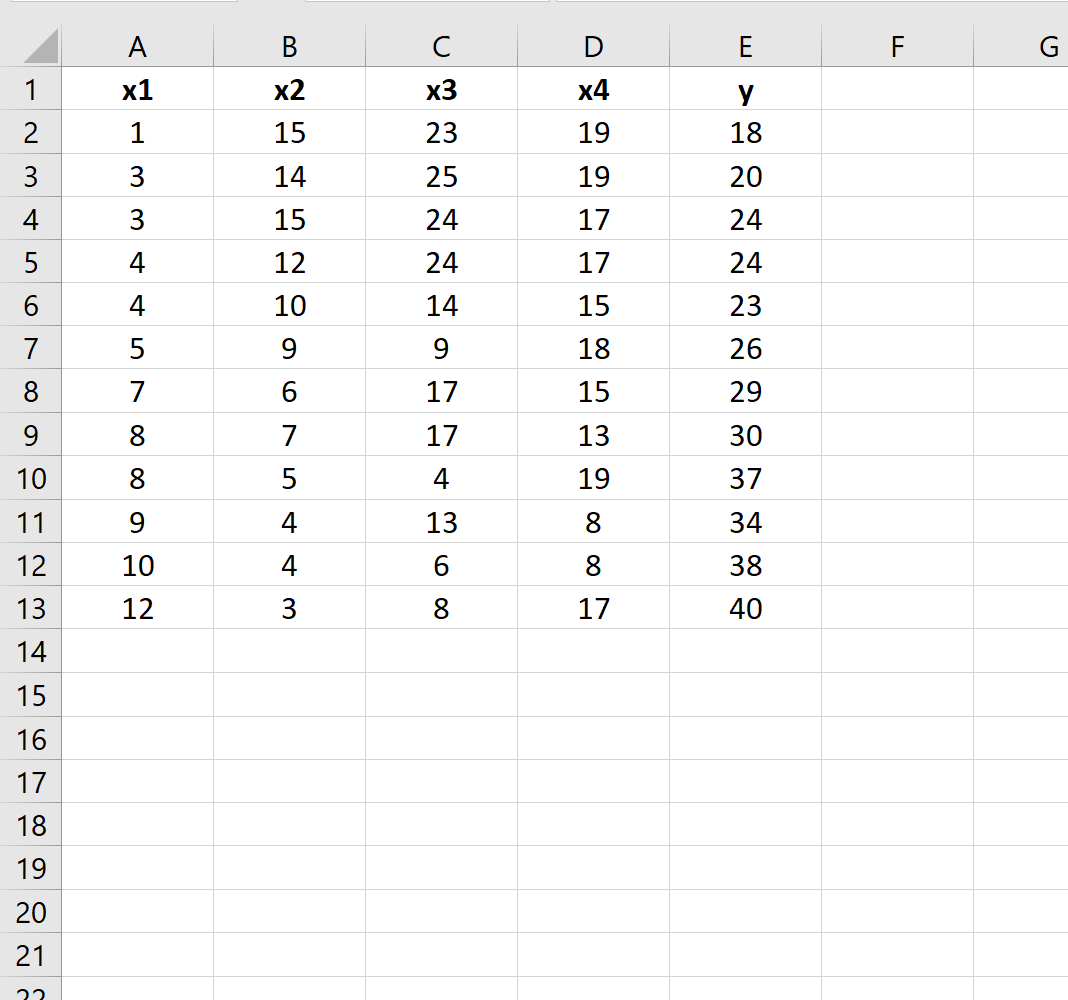
Załóżmy, że chcemy ustalić, czy istnieje różnica między następującymi dwoma modelami regresji:
Model kompletny: y = β 0 + β 1 x 1 + β 2 x 2 + β 3 x 3 + β 4 x 4
Model zredukowany: y = β 0 + β 1 x 1 + β 2 x 2
Dla każdego modelu możemy wykonać wielokrotną regresję liniową w programie Excel, aby uzyskać następujący wynik:
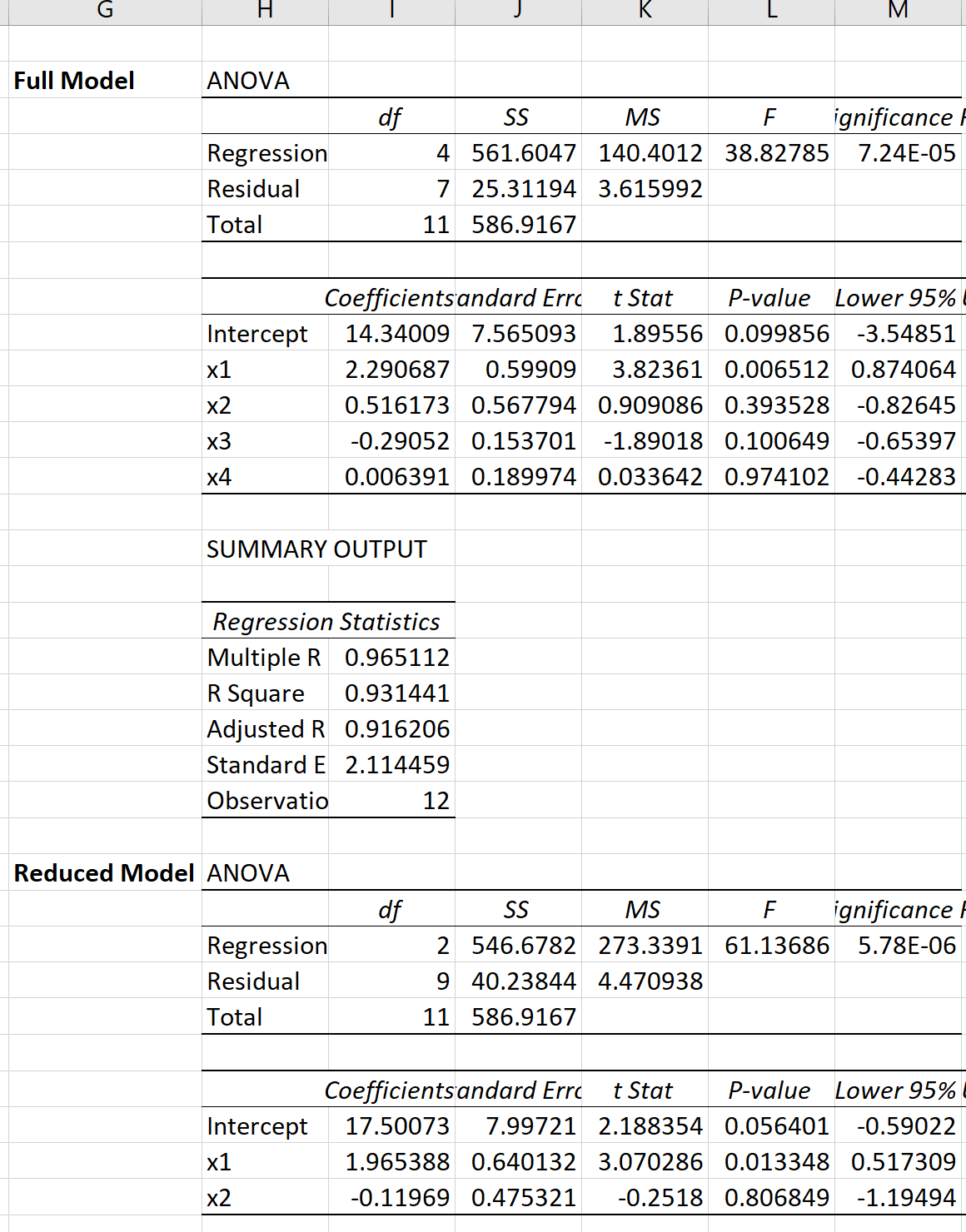
Możemy następnie użyć następującego wzoru do obliczenia statystyki testu F dla częściowego testu F:
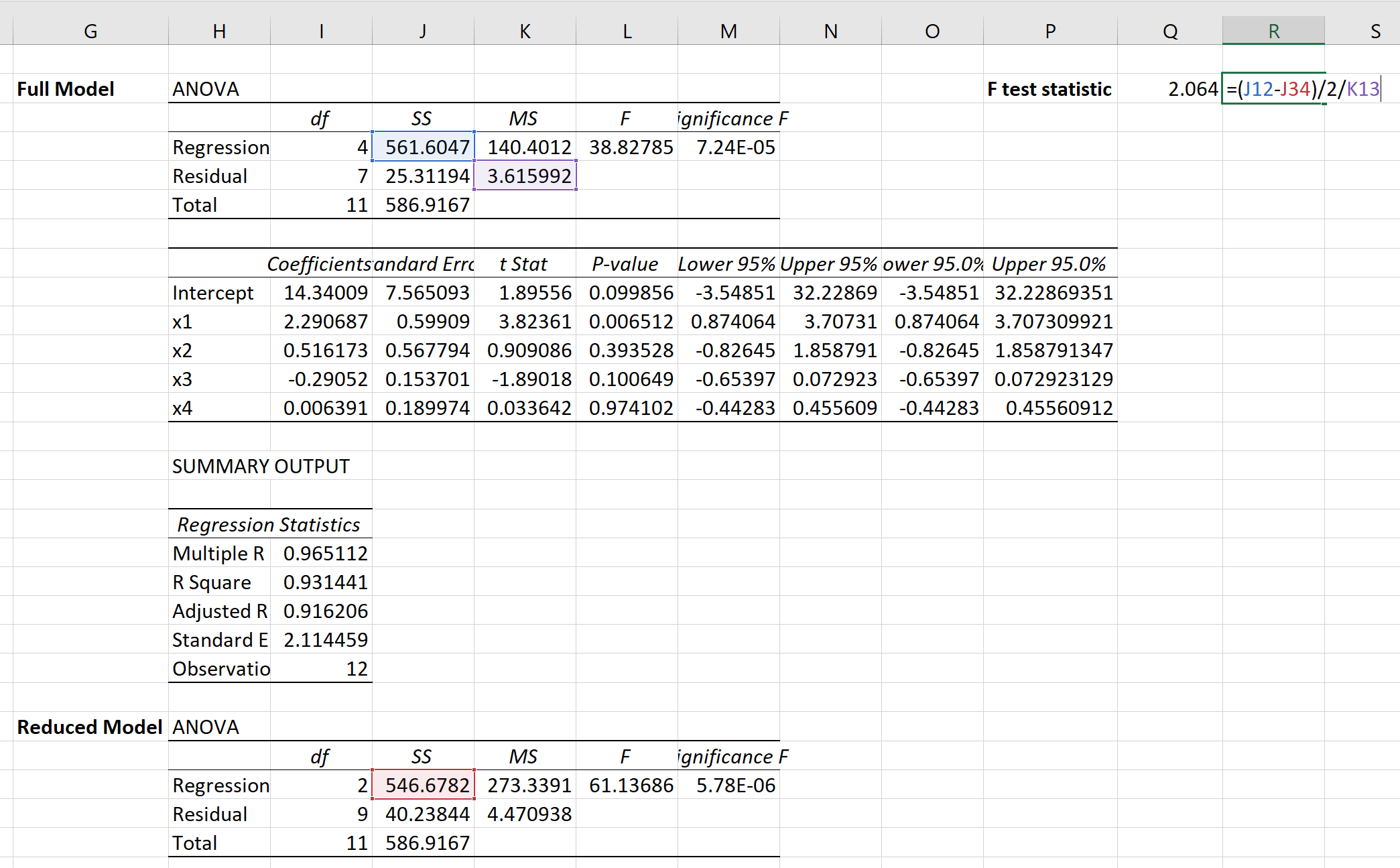
Statystyka testowa okazuje się wynosić 2,064 .
Możemy następnie użyć następującego wzoru do obliczenia odpowiedniej wartości p:
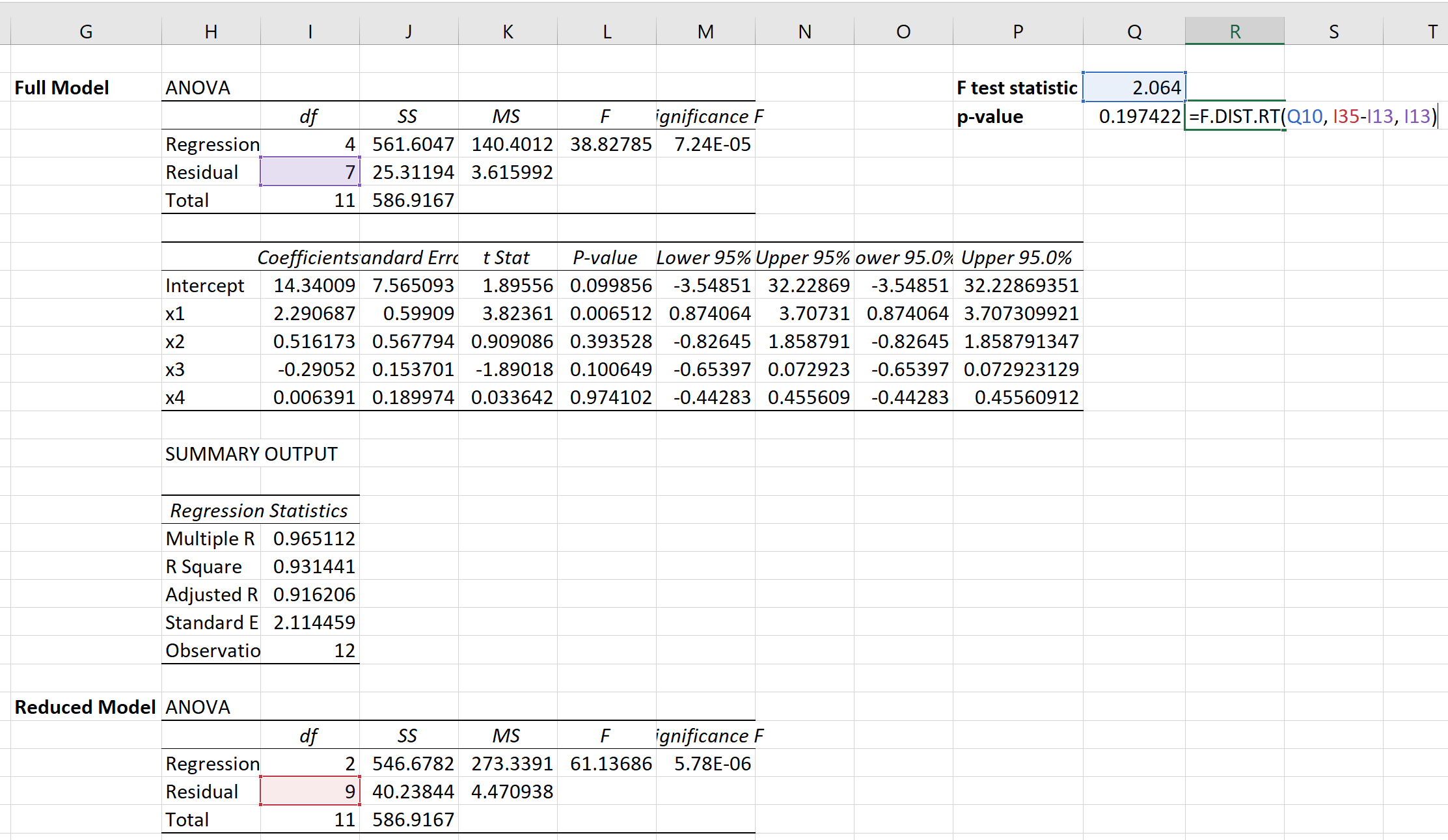
Wartość p wynosi 0,1974 .
Ponieważ ta wartość p jest nie mniejsza niż 0,05, nie uda nam się odrzucić hipotezy zerowej. Oznacza to, że nie mamy wystarczających dowodów, aby stwierdzić, że którakolwiek ze zmiennych predykcyjnych x3 lub x4 jest istotna statystycznie.
Innymi słowy, dodanie x3 i x4 do modelu regresji nie poprawia znacząco dopasowania modelu.
Dodatkowe zasoby
Jak wykonać prostą regresję liniową w programie Excel
Jak wykonać wielokrotną regresję liniową w programie Excel
Jak obliczyć błąd standardowy regresji w programie Excel
o autorze
Dr Benjamin Anderson
Cześć, jestem Benjamin i jestem emerytowanym profesorem statystyki, który został oddanym nauczycielem Statorials. Dzięki bogatemu doświadczeniu i wiedzy specjalistycznej w dziedzinie statystyki chętnie dzielę się swoją wiedzą, aby wzmocnić pozycję uczniów za pośrednictwem Statorials. Wiedzieć więcej