Częstotliwość bezwzględna
W tym artykule wyjaśniono znaczenie częstotliwości bezwzględnej w statystyce. W ten sposób dowiesz się, jak uzyskać częstotliwość bezwzględną zbioru danych, dwa rozwiązane ćwiczenia, a ponadto różnice w stosunku do innych typów częstotliwości statystycznych.
Jaka jest częstotliwość bezwzględna?
W statystyce częstotliwość bezwzględna oznacza, ile razy dana wartość pojawia się w zbiorze danych. Mówiąc najprościej, częstotliwość bezwzględna to liczba powtórzeń wyniku.
Na przykład, jeśli siedem osób w ankiecie odpowiedziało, że ich ulubionym kolorem jest czerwony, wówczas bezwzględna częstotliwość występowania koloru czerwonego wynosi 7.
Dlatego suma częstotliwości bezwzględnych wszystkich wartości jest równa całkowitej liczbie danych w próbie statystycznej.
Ogólnie rzecz biorąc, litera f z indeksem dolnym i jest używana do przedstawienia częstotliwości bezwzględnej wartości i , więc symbolem częstotliwości bezwzględnej jest fi .
Jak obliczyć częstotliwość bezwzględną
Aby uzyskać częstotliwości bezwzględne zbioru danych, należy wykonać następujące kroki:
- Jeśli zmienna jest dyskretna, utwórz tablicę ze wszystkich różnych wartości występujących w zbiorze danych, czyli umieść każdą inną wartość w wierszu tabeli.
- Jeśli zmienna jest ciągła, pogrupuj dane w przedziały i utwórz tabelę ze wszystkimi przedziałami.
- Policz, ile razy dana wartość pojawia się w zbiorze danych i zapisz wynik w tabeli częstości.
- Powtórz poprzedni krok dla każdej innej wartości w przykładowych danych.
Przykłady częstotliwości bezwzględnej
Kiedy już zapoznamy się z definicją częstotliwości bezwzględnej i teorią jej obliczania, zobaczymy dwa przykłady, abyś wiedział, jak to się robi. W pierwszym przykładzie wyznaczymy częstotliwości bezwzględne zmiennej dyskretnej, a w drugim przykładzie zmiennej ciągłej, ponieważ procedura różni się nieznacznie w zależności od przypadku.
Przykład 1: zmienna dyskretna
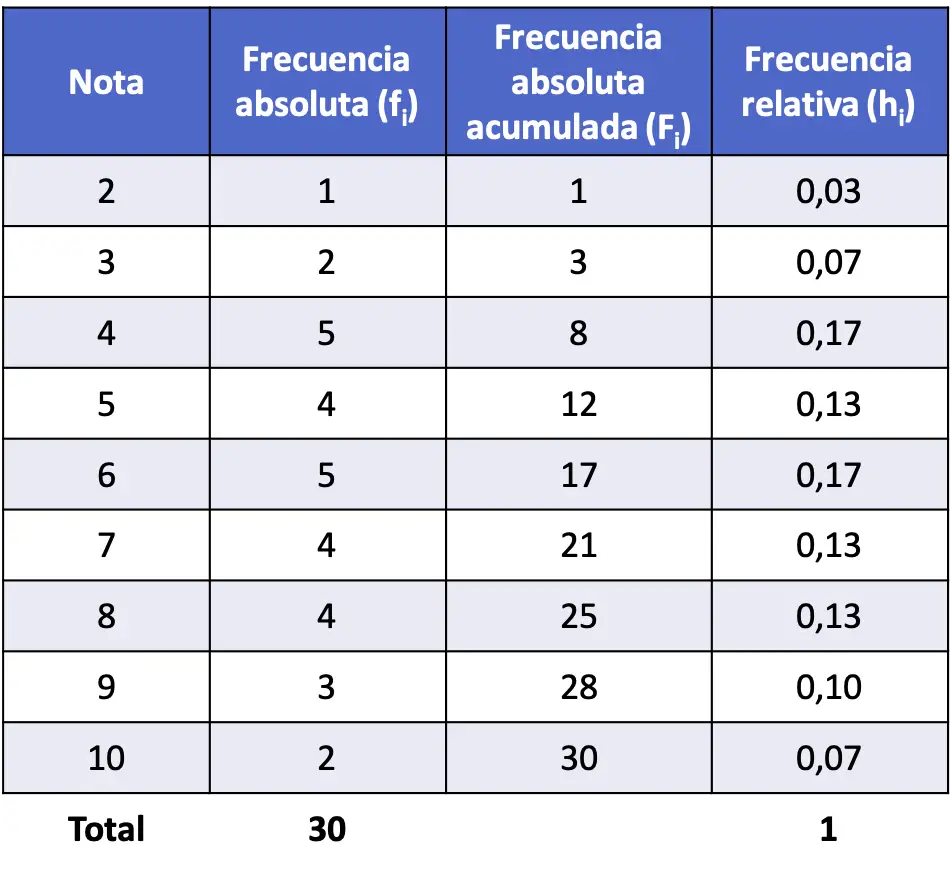
- Oceny uzyskane ze statystyki w klasie 30 uczniów przedstawiają się następująco. Jaka jest bezwzględna częstotliwość każdej nuty?
![]()
![]()
![]()
W tym przypadku jest to zmienna dyskretna, ponieważ mogą występować tylko liczby całkowite, więc nie ma potrzeby grupowania ich w przedziały.
Policz więc, ile razy pojawia się każda wartość i zapisz ją w tabeli częstości:

Należy zauważyć, że suma wszystkich częstotliwości bezwzględnych jest równa całkowitej liczbie punktów danych. Jeśli ta zasada nie będzie przestrzegana, oznacza to, że zapomniałeś policzyć niektóre dane.
Przykład 2: zmienna ciągła
- Zmierzono wzrost 20 osób i uzyskano wyniki podane poniżej. Podziel dane na przedziały i znajdź bezwzględną częstotliwość każdego przedziału.
![]()
![]()
Dane w tej próbie mają rozkład ciągły, ponieważ liczby mogą być dziesiętne. Dlatego musimy pogrupować dane w interwały, w tym przypadku zrobimy interwały o szerokości 10 dziesiątych.
Zatem liczymy liczbę danych w każdym przedziale i przedstawiamy częstotliwości bezwzględne w tabeli:

Częstotliwość bezwzględna i skumulowana częstotliwość bezwzględna
Jak sama nazwa wskazuje, skumulowana częstotliwość bezwzględna to inny rodzaj częstotliwości stosowany w statystyce i powiązany z częstotliwością bezwzględną.
Skumulowana częstotliwość bezwzględna wartości jest równa sumie częstotliwości bezwzględnej samej wartości plus częstotliwości bezwzględnych wszystkich poprzednich wartości.
Jako przykład możesz zobaczyć poniżej obliczenie skumulowanych częstotliwości bezwzględnych pierwszego ćwiczenia rozwiązanego powyżej:

Częstotliwość bezwzględna i częstotliwość względna
W statystyce częstotliwość względna to inny rodzaj częstotliwości niż dwie przedstawione powyżej, ponieważ reprezentuje procent każdej wartości w porównaniu do całości. Dlatego w tej sekcji zobaczymy różnicę między tymi dwoma koncepcjami.
Różnica między częstotliwością bezwzględną a częstotliwością względną polega na tym, że częstotliwość bezwzględna to bezwzględna liczba wartości w próbce, podczas gdy częstotliwość względna to proporcja każdej wartości do całości.
Dlatego częstotliwość względną oblicza się, dzieląc częstotliwość bezwzględną przez całkowitą liczbę danych.