Częstotliwość (statystyka)

W tym artykule wyjaśniono, czym jest pojęcie częstotliwości w statystyce. W ten sposób znajdziesz definicję częstotliwości w statystykach, różne istniejące rodzaje częstotliwości i wreszcie, jak utworzyć tabelę częstości.

Co to jest częstotliwość w statystykach?

W statystykach częstotliwość oznacza, ile razy dana wartość pojawia się w zbiorze danych. Mówiąc najprościej, częstotliwość to liczba powtórzeń wartości w próbce statystycznej.

Na przykład, jeśli w ankiecie pięć osób odpowiedziało, że ich ulubionym kolorem jest niebieski, to częstotliwość występowania koloru niebieskiego wynosi 5.

Ogólnie rzecz biorąc, w statystyce litera f z indeksem i jest używana do przedstawienia częstotliwości wartości i , więc symbolem częstotliwości jest _fi .

Suma wszystkich częstotliwości daje całkowitą liczbę danych w próbce. Dlatego w każdym badaniu statystycznym zawsze obowiązuje następujący wzór:

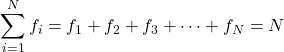
Złoto

jest częstotliwością wartości

I

to całkowita liczba obserwacji.

Rodzaje częstotliwości w statystyce

W statystykach różne typy częstotliwości są następujące:

• Częstotliwość bezwzględna : odpowiada liczbie wystąpień danej wartości w próbce statystycznej.
• Skumulowana częstotliwość bezwzględna : Obliczana poprzez dodanie częstotliwości bezwzględnej wartości oraz częstotliwości bezwzględnych wszystkich mniejszych wartości.
• Częstotliwość względna : jest to częstotliwość bezwzględna podzielona przez całkowitą liczbę danych.
• Skumulowana częstotliwość względna : równa sumie częstotliwości względnej danej wartości oraz częstotliwości względnych wszystkich niższych wartości.

W poniższej sekcji możesz zobaczyć, jak obliczany jest każdy typ częstotliwości.

Tabela częstotliwości

Zazwyczaj w statystyce obliczenia częstotliwości próbki danych podsumowuje się w tabeli częstości. Poniżej znajduje się przykład krok po kroku, dzięki czemu możesz zobaczyć, jak to zrobić.

• Oceny uzyskane z przedmiotu statystyka w klasie 30 uczniów przedstawiają się następująco. Utwórz tabelę częstości zbioru danych.

Ponieważ wszystkie liczby mogą być tylko liczbami całkowitymi, jest to zmienna dyskretna. Nie jest zatem konieczne grupowanie danych w przedziały.

Musimy zatem skonstruować tabelę, w której każda inna wartość będzie wierszem. Ponadto musimy znaleźć częstotliwość bezwzględną każdej wartości. W tym celu wystarczy policzyć, ile razy dana wartość pojawia się w próbce danych.

Należy pamiętać, że suma wszystkich częstotliwości bezwzględnych jest równa całkowitej liczbie danych. Jeśli zasada ta nie będzie przestrzegana, oznacza to, że zapomniałeś podać pewnych informacji.

Teraz, gdy znamy częstotliwość bezwzględną, musimy znaleźć skumulowaną częstotliwość bezwzględną. Do tego obliczenia mamy dwie możliwości: albo dodajemy częstotliwość bezwzględną wartości plus wszystkie częstotliwości bezwzględne najmniejszych wartości, albo odwrotnie, dodajemy częstotliwość bezwzględną wartości plus skumulowaną częstotliwość bezwzględną poprzedniej wartości.

Skumulowana częstotliwość bezwzględna ostatniej wartości zawsze odpowiada całkowitej liczbie danych. Możesz skorzystać z tej sztuczki, aby sprawdzić, czy obliczenia są prawidłowe.

Następnie musimy określić częstotliwość względną, którą obliczamy dzieląc częstotliwość bezwzględną przez całkowitą liczbę punktów danych (30):

Należy pamiętać, że suma wszystkich częstotliwości względnych zawsze wynosi 1, w przeciwnym razie oznacza to, że niektóre obliczenia w tabeli częstości są błędne.

Na koniec wystarczy wyodrębnić skumulowaną częstotliwość względną. Aby to zrobić, należy dodać częstotliwość względną danej wartości plus wszystkie poprzednie częstotliwości względne lub, co sprowadza się do tego samego, poprzednią skumulowaną częstotliwość względną:

Krótko mówiąc, tabela częstotliwości ze wszystkimi częstotliwościami problematycznych danych wygląda następująco: