Częstotliwość względna

W tym artykule dowiesz się, czym jest częstotliwość względna w statystyce, jak uzyskać częstotliwość względną oraz dwa rozwiązane krok po kroku ćwiczenia dotyczące częstotliwości względnej.

Co to jest częstotliwość względna?

W statystyce częstotliwość względna jest miarą wskazującą, ile razy dana wartość pojawia się w próbce danych w postaci proporcji lub wartości procentowej. Dokładniej, częstotliwość względna jest równa częstotliwości bezwzględnej podzielonej przez całkowitą liczbę danych.

Na przykład, jeśli częstotliwość bezwzględna wartości wynosi 15 i łącznie istnieje 100 punktów danych, częstotliwość względna tej wartości wynosi 0,15 (15/100 = 0,15).

Ogólnie rzecz biorąc, symbol h _i jest używany do przedstawienia częstotliwości względnej. Chociaż w społeczności statystycznej nadal nie ma konsensusu, możesz zobaczyć względną częstotliwość reprezentowaną przez inny symbol.

Jak obliczyć częstotliwość względną

Częstotliwość względna jest równa częstotliwości bezwzględnej podzielonej przez całkowitą liczbę danych. Dlatego, aby obliczyć częstotliwość względną, należy najpierw znaleźć częstotliwość bezwzględną, a następnie podzielić ją przez całkowitą liczbę obserwacji.

Zatem wzór na częstotliwość względną jest następujący:

Złoto:

• 

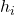
  jest częstotliwością względną.

• 

  jest częstotliwością bezwzględną.

• 

  to całkowita liczba danych.

Z drugiej strony, aby obliczyć częstotliwość względną w procentach , czyli częstotliwość względną wyrażoną w procentach, wystarczy pomnożyć poprzedni wzór przez 100:

Przykłady częstotliwości względnej

Po zapoznaniu się z definicją częstotliwości względnej poniżej znajdują się dwa przykłady z życia wzięte, dzięki którym możesz zobaczyć, jak obliczany jest ten typ częstotliwości. W pierwszym przykładzie wyznaczana jest częstotliwość względna zmiennej dyskretnej, a w drugim przykładzie zmiennej ciągłej.

Przykład 1: zmienna dyskretna

• Oceny uzyskane z przedmiotu statystyka w klasie 30 uczniów przedstawiają się następująco. Jaka jest względna częstotliwość każdej nuty?

Zmienna w tym ćwiczeniu jest dyskretna, ponieważ dane mogą być tylko liczbami całkowitymi; dlatego nie ma potrzeby grupowania danych w interwały.

Aby znaleźć częstotliwość względną, musimy najpierw określić częstotliwość bezwzględną. Dlatego konstruujemy tabelę częstości i obliczamy częstotliwość bezwzględną dla każdej innej wartości:

Teraz, gdy obliczyliśmy częstotliwość bezwzględną, możemy obliczyć częstotliwość względną. Aby to zrobić, po prostu podziel każdą częstotliwość bezwzględną przez całkowitą liczbę danych (30):

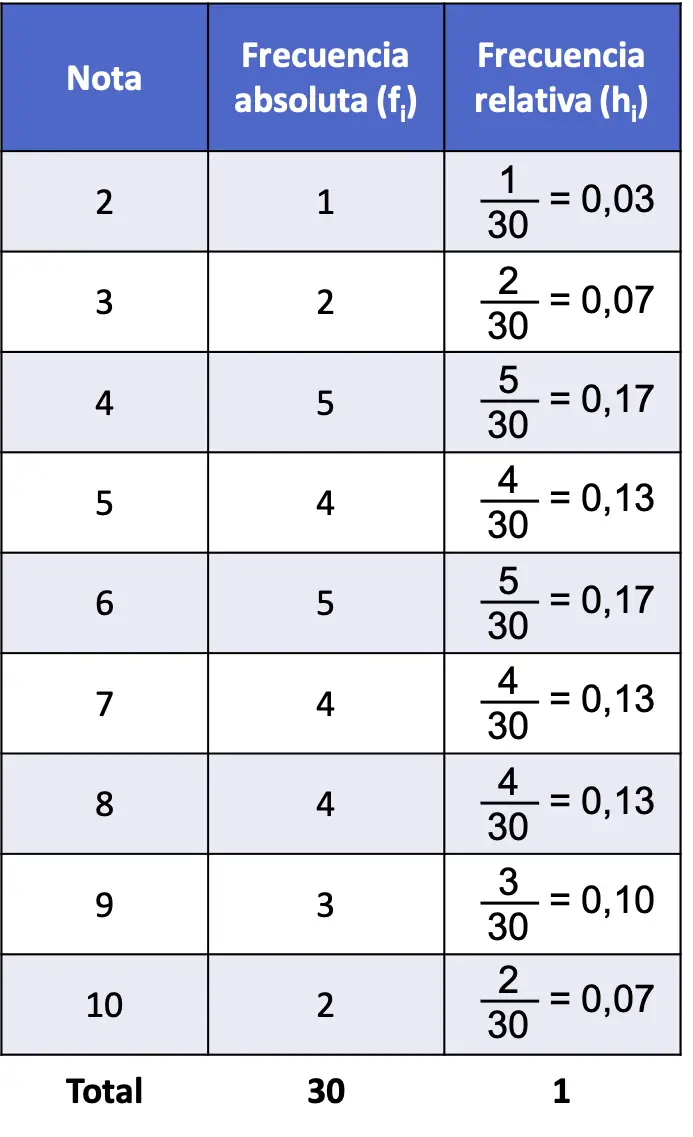
Zatem tabela częstości problemu z częstotliwością bezwzględną i częstotliwością względną jest następująca:

Należy pamiętać, że suma wszystkich częstotliwości względnych zawsze daje 1, w przeciwnym razie oznacza to, że niektóre obliczenia są błędne.

Przykład 2: zmienna ciągła

• Zmierzono wzrost 20 osób i uzyskano wyniki podane poniżej. Podziel dane na przedziały i znajdź względną częstotliwość każdego przedziału.

Dane w tej próbie statystycznej należą do zmiennej ciągłej, ponieważ są dziesiętne i dlatego zmienna może przyjmować dowolną wartość. Zatem przed wykonaniem obliczeń częstotliwości najpierw pogrupujemy dane w przedziały o amplitudzie 10 dziesiątych.

Następnie tworzymy tabelę częstości z częstotliwością bezwzględną każdego przedziału:

Kiedy już znajdziemy częstotliwość bezwzględną, możemy uzyskać częstotliwość względną każdego przedziału, dzieląc jego częstotliwość bezwzględną przez całkowitą liczbę danych (20):

Skumulowana częstotliwość względna

Jak sama nazwa wskazuje, skumulowana częstotliwość względna to inny rodzaj częstotliwości używany w statystykach i obliczany na podstawie częstotliwości względnej.

Dokładniej, skumulowana częstotliwość względna wartości jest równa sumie częstotliwości względnej samej wartości plus częstotliwości względnych wszystkich mniejszych wartości.

Aby można było zobaczyć, w jaki sposób uzyskiwana jest skumulowana częstotliwość względna, skumulowana częstotliwość względna zbioru danych w pierwszym przykładzie została obliczona poniżej: