Czy przyczynowość implikuje korelację? (3 przykłady)

Powszechnie wiadomo, że korelacja nie oznacza związku przyczynowego .

Dla prostego przykładu, gdybyśmy co roku zbierali dane na temat całkowitej liczby absolwentów szkół średnich i całkowitego spożycia pizzy w Stanach Zjednoczonych, odkrylibyśmy, że te dwie zmienne są silnie skorelowane:

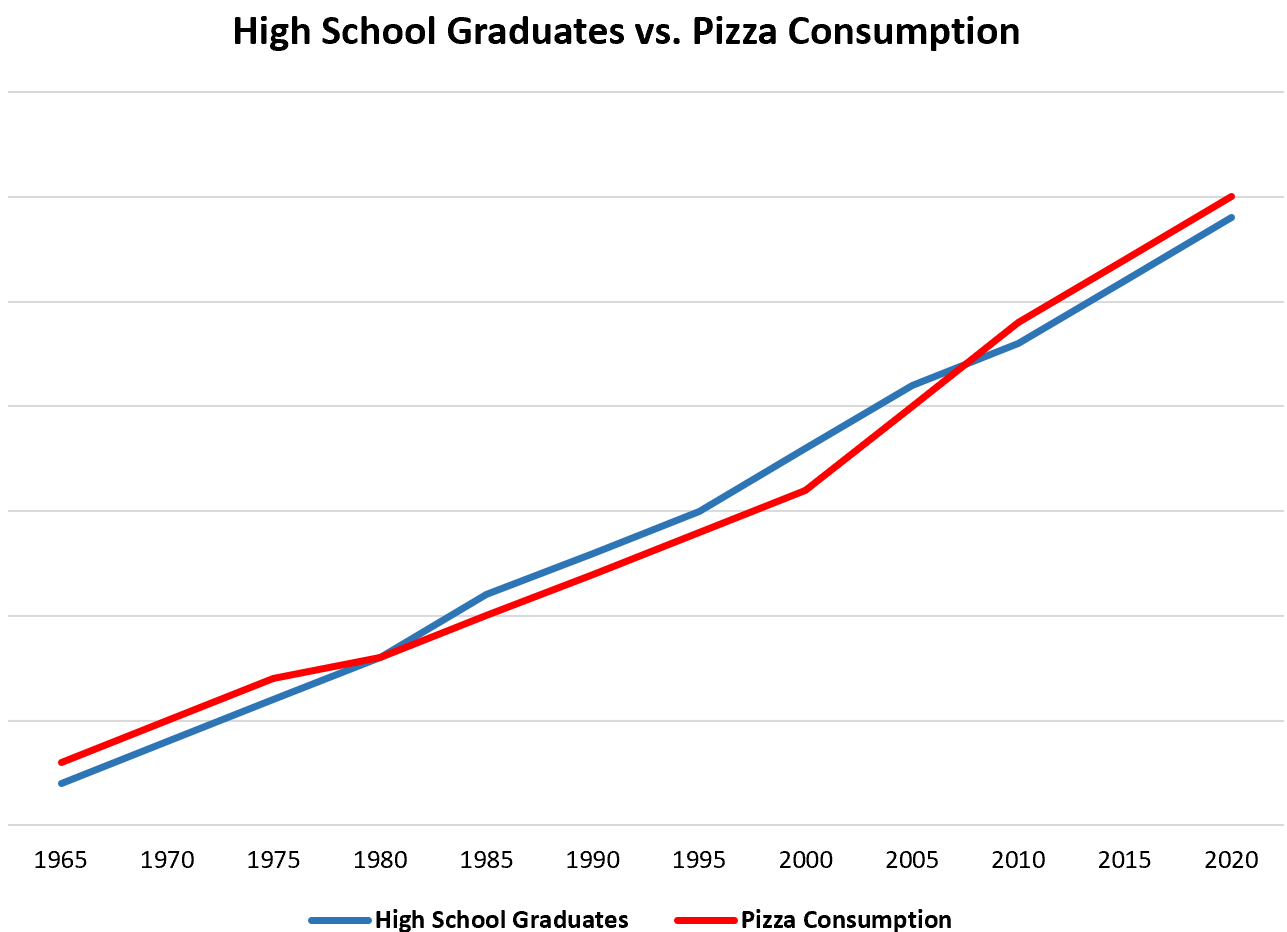
Nie oznacza to jednak, że wzrost liczby absolwentów szkół średnich prowadzi do wzrostu spożycia pizzy.

Najbardziej prawdopodobnym wyjaśnieniem jest to, że populacja Stanów Zjednoczonych z biegiem czasu wzrosła, co oznacza, że wraz ze wzrostem populacji wzrasta liczba osób z dyplomem szkoły średniej i całkowita ilość spożywanej pizzy.

Ale co ze stwierdzeniem przeciwnym: czy przyczynowość implikuje korelację?

Jeśli jedna zmienna powoduje inną zmienną, czy to koniecznie oznacza, że te dwie zmienne będą skorelowane?

Krótka odpowiedź: nie.

Poniższe przykłady pokazują dlaczego.

Przykład 1: zależność kwadratowa

Załóżmy, że zmienna X powoduje, że zmienna Y przyjmuje wartość równą X ² .

Na przykład:

• Jeśli X = -10, to Y = -10 ² = 100
• Jeśli X = 0, to Y = 0 ² = 0
• Jeśli X = 10, to Y = 10 ² = 100

I tak dalej.

Jeśli narysujemy zależność pomiędzy X i Y, będzie ona wyglądać następująco:

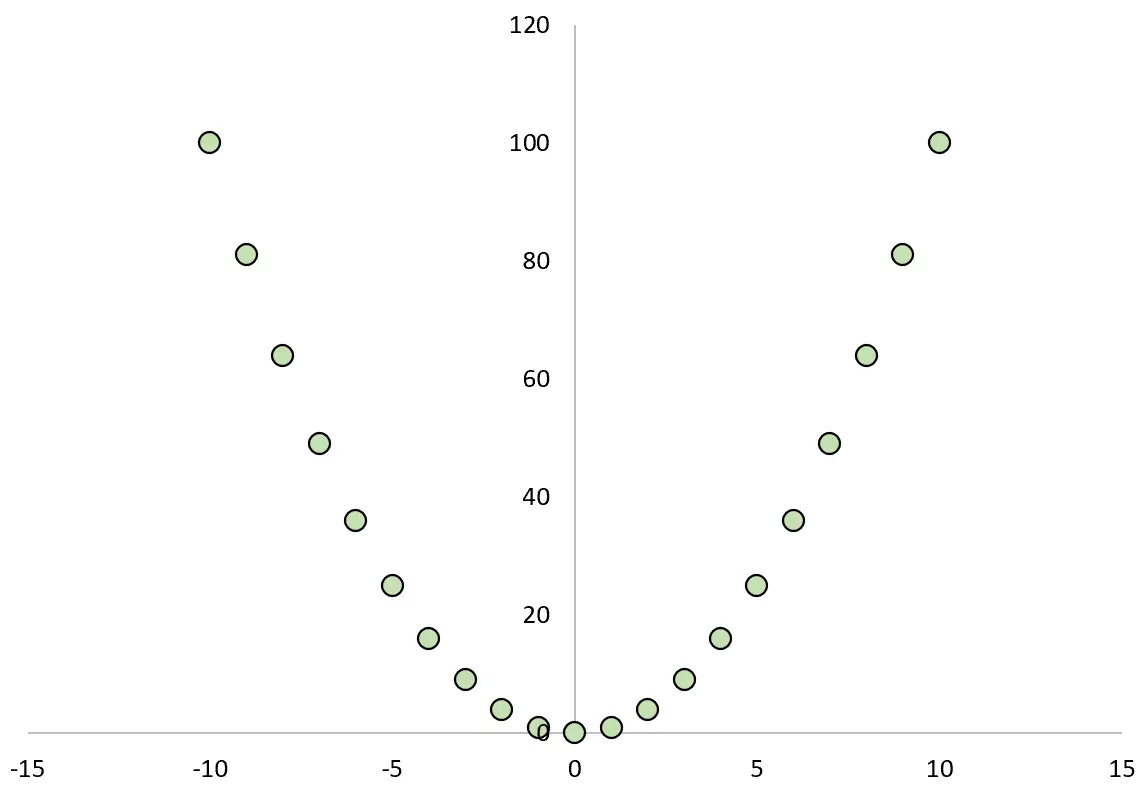
Gdybyśmy obliczyli współczynnik korelacji Pearsona między dwiema zmiennymi, odkrylibyśmy, że korelacja wynosi zero .

Chociaż X powoduje Y, korelacja liniowa między dwiema zmiennymi wynosi zero.

Przykład 2: relacja kwartalna

Załóżmy, że zmienna X powoduje, że zmienna Y przyjmuje wartość równą X ⁴ .

Na przykład:

• Jeśli X = -10, to Y = -10 ⁴ = 10 000
• Jeśli X = 0, to Y = 0 ⁴ = 0
• Jeśli X = 10, to Y = 10 ⁴ = 10 000

I tak dalej.

Jeśli narysujemy zależność pomiędzy X i Y, będzie ona wyglądać następująco:

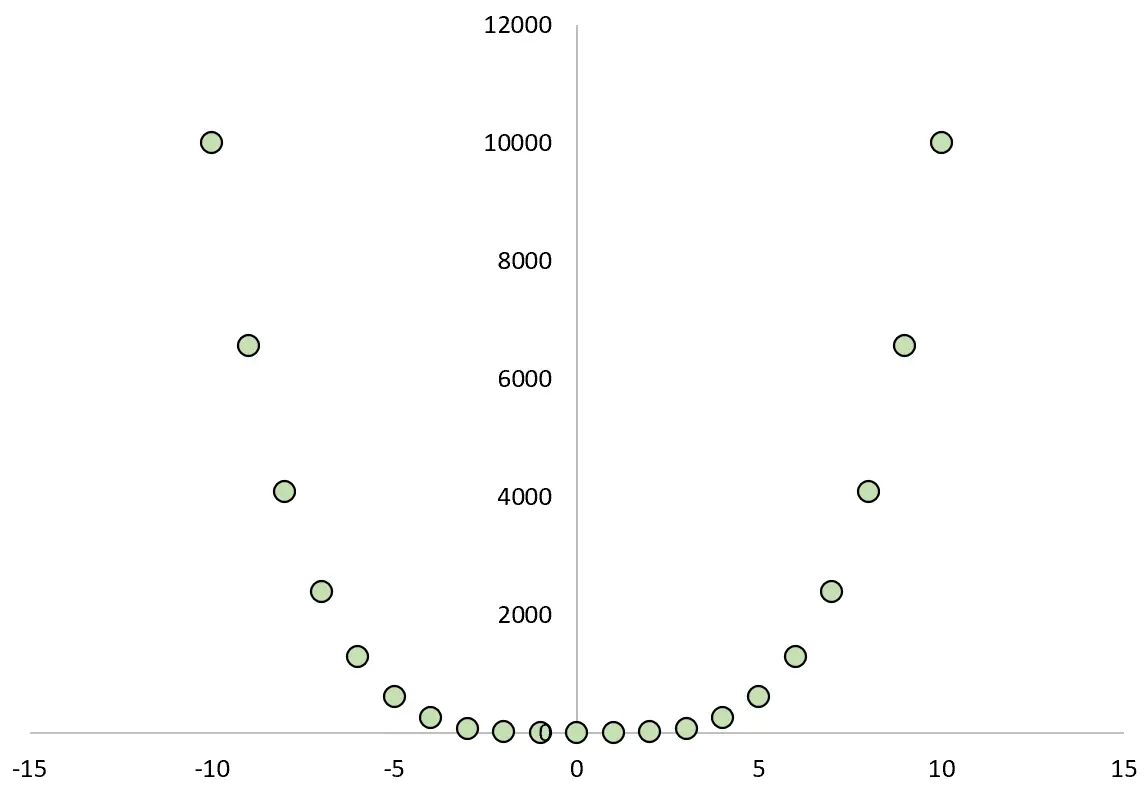
Gdybyśmy obliczyli współczynnik korelacji Pearsona między dwiema zmiennymi, odkrylibyśmy, że korelacja wynosi zero .

Wiemy, że X powoduje Y, ale korelacja liniowa między dwiema zmiennymi wynosi zero.

Przykład 3: zależność cosinus

Załóżmy, że zmienna X powoduje, że zmienna Y przyjmuje wartość równą cos(X).

Na przykład:

• Jeśli X = -10, to Y = cos(-10) = -0,83907
• Jeśli X = 0, to Y = cos(0) = 1
• Jeśli X = 10, to Y = cos(10) = -0,83907

I tak dalej.

Jeśli narysujemy zależność pomiędzy X i Y, będzie ona wyglądać następująco:

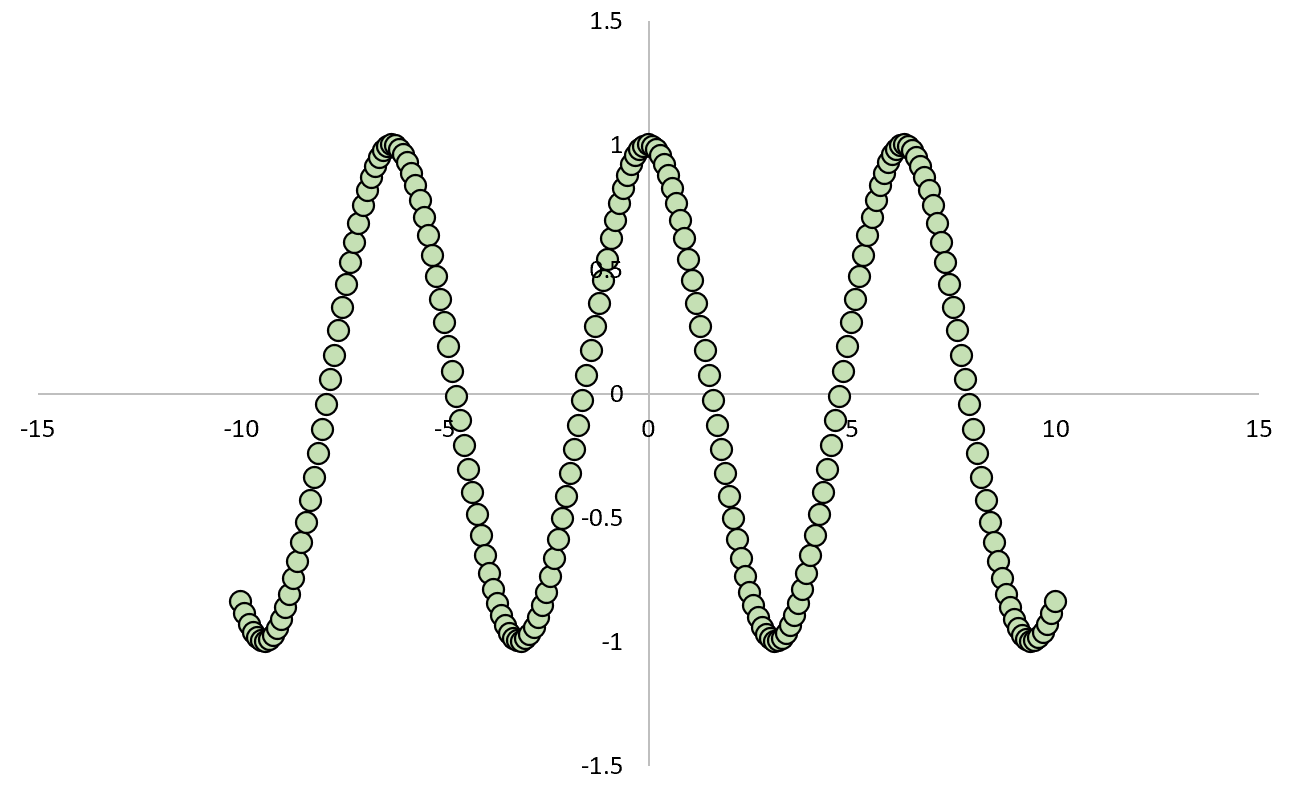
Gdybyśmy obliczyli współczynnik korelacji Pearsona między dwiema zmiennymi, odkrylibyśmy, że korelacja wynosi zero .

Wiemy, że X powoduje Y, ale korelacja liniowa między dwiema zmiennymi wynosi zero.

Dodatkowe zasoby

Poniższe samouczki dostarczają dodatkowych informacji na temat korelacji i związku przyczynowego:

Korelacja nie implikuje związku przyczynowego: 5 konkretnych przykładów
Wprowadzenie do współczynnika korelacji Pearsona
Odwrotna przyczynowość: definicja i przykłady