Decyle
W tym artykule wyjaśniamy, czym są decyle i jak są obliczane. Znajdziesz tu również kilka rozwiązanych przykładów obliczeń decyli krok po kroku, a dodatkowo będziesz mógł obliczyć decyle dowolnej próbki statystycznej za pomocą kalkulatora online.
Co to są decyle?
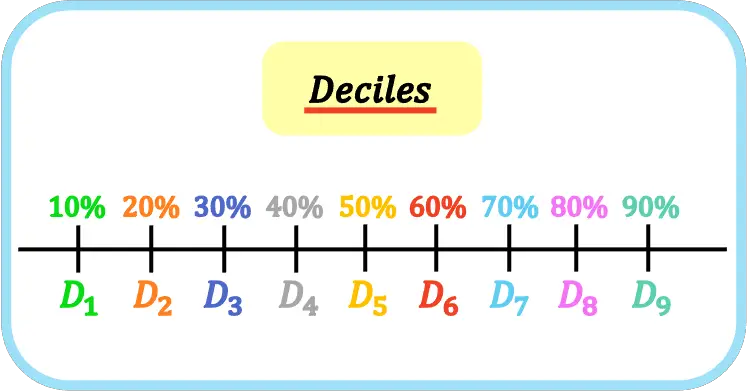
W statystyce decyle to dziewięć wartości, które dzielą zbiór uporządkowanych danych na dziesięć równych części. Tak więc pierwszy, drugi, trzeci… decyl reprezentuje 10%, 20%, 30%… próbki lub populacji.
Na przykład czwarta wartość decyla jest większa niż 40% danych, ale niższa niż pozostałe dane.
Decyle są reprezentowane przez wielką literę D i indeks decyli, to znaczy pierwszy decyl to D 1 , drugi decyl to D 2 , trzeci decyl to D 3 itd.
👉 Możesz skorzystać z poniższego kalkulatora, aby obliczyć decyle dla dowolnego zbioru danych.
Należy zauważyć, że decyle są miarą położenia niecentralnego w taki sam sposób, jak kwartyle, kwintyle i percentyle. Znaczenie każdego z tych typów kwantyli możesz sprawdzić na naszej stronie internetowej.
Dodatkowo piąty decyl jest odpowiednikiem mediany i drugiego kwartyla, ponieważ dzielą one cały zbiór danych na dwie równe części.
Jak obliczyć decyle
Aby obliczyć pozycję decylową serii danych statystycznych, należy pomnożyć liczbę decyli przez sumę całkowitej liczby danych plus jeden i podzielić wynik przez dziesięć.
Wzór na decyl jest zatem następujący:
![]()
Uwaga: ten wzór informuje nas o pozycji decyla, a nie o jego wartości. Decylem będą dane znajdujące się na pozycji otrzymanej ze wzoru.
Czasami jednak wynik tej formuły da nam liczbę dziesiętną, dlatego musimy rozróżnić dwa przypadki w zależności od tego, czy wynik jest liczbą dziesiętną, czy nie:
- Jeżeli wynikiem wzoru jest liczba bez części dziesiętnej , decylem jest dana znajdująca się na pozycji określonej we wzorze powyżej.
- Jeżeli wynikiem wzoru jest liczba zawierająca część dziesiętną , wartość decyla oblicza się według następującego wzoru:
![]()
Gdzie x i oraz x i+1 to numery pozycji, pomiędzy którymi znajduje się liczba uzyskana według pierwszego wzoru, a d to część dziesiętna liczby uzyskanej według pierwszego wzoru.
Teraz możesz pomyśleć, że uzyskanie decyli próbki statystycznej jest skomplikowane, ale w praktyce jest całkiem proste. Jeśli przeczytasz poniższe dwa przykłady, z pewnością zrozumiesz to znacznie lepiej.
Uwaga : społeczność naukowa nie jest do końca zgodna co do sposobu obliczania decyli, dlatego można znaleźć książki statystyczne, które wyjaśniają to nieco inaczej.
Przykład obliczenia decyli
Jak widzieliście powyżej, obliczenie decyli zależy od tego, czy liczba, którą daje nam pierwszy wzór, jest dziesiętna, czy nie, dlatego poniżej przygotowaliśmy dwa rozwiązane przykłady, po jednym dla każdego przypadku. W każdym razie pamiętajcie, że jeśli macie jakieś pytania dotyczące składu decyli, możecie je zadać w komentarzach.
Przykład 1
- Mając następujące dane, od najmniejszych do największych, znajdź pierwszy, trzeci i ósmy decyl próbki.

Dane w tym ćwiczeniu są już posortowane, więc nie ma potrzeby zmiany kolejności, w przeciwnym razie musielibyśmy najpierw posortować dane od najmniejszego do największego.
Jak wyjaśniono powyżej, wzór pozwalający znaleźć położenie decyli jest następujący:
![]()
Wielkość próby w tym ćwiczeniu wynosi 29 obserwacji, więc aby obliczyć położenie pierwszego decyla, należy zastąpić n 29 i k :
![]()
Wynikiem wzoru jest liczba 3, więc pierwszy decyl będzie na trzeciej pozycji uporządkowanej listy, a wartość ta odpowiada 85.
Teraz ponownie stosujemy tę samą procedurę, ale z trzecim decylem. Używamy wzoru, zastępując k liczbą 3:
![]()
Trzeci decyl będzie zatem elementem na dziewiątej pozycji, czyli 97.
Na koniec wykonujemy ten sam proces, ale wstawiamy 8 do wzoru, aby określić ósmy decyl:
![]()
Ósmy decyl będzie liczbą znajdującą się na pozycji 24 uporządkowanej listy danych, więc ósmy decyl to 131.
Przykład 2
- Na podstawie danych w poniższej tabeli oblicz decyle 4, 7 i 9.

Podobnie jak w poprzednim przykładzie, aby obliczyć położenie decyli, należy skorzystać ze wzoru:
![]()
W tym przypadku wielkość próby wynosi 42, więc aby znaleźć pozycję czwartego decyla, należy zastąpić parametr n przez 42, a k przez 4:
![]()
Ale tym razem otrzymaliśmy liczbę dziesiętną ze wzoru, więc musimy zastosować następujący wzór, aby obliczyć dokładny decyl:
![]()
Liczba uzyskana z pierwszego wzoru wynosi 17,2, zatem czwarty decyl mieści się pomiędzy podanym siedemnastym a osiemnastym, czyli odpowiednio 109 i 112. Zatem x i wynosi 109, x i+ 1 wynosi 112, a d jest częścią dziesiętną. otrzymanej liczby, tj. 0,2.
![]()
Powtarzamy ten sam proces, aby znaleźć siódmy decyl. Najpierw obliczamy położenie decyla:
![]()
Ze wzoru otrzymaliśmy liczbę 30,1, co oznacza, że decyl będzie znajdował się pomiędzy pozycjami 30 a 31, których wartości wynoszą 154 i 159. Obliczenie dokładnego decyla jest zatem następujące:
![]()
Na koniec ponownie stosujemy tę samą metodę, aby uzyskać dziewiąty decyl. Określamy położenie decyla:
![]()
Uzyskana liczba jest dziesiętna i mieści się w przedziale od 38 do 39, której pozycje odpowiadają wartościom 189 i 196. Zatem obliczenie decyla 9 jest następujące:
![]()
Kalkulator decyli
Podłącz zestaw danych statystycznych do poniższego kalkulatora, aby obliczyć decyle. Dane należy oddzielić spacją i wprowadzić z użyciem kropki jako separatora dziesiętnego.
Decyle w danych pogrupowanych
Aby obliczyć decyle, gdy dane są pogrupowane w przedziały , musimy najpierw znaleźć przedział lub przedział, w którym mieści się decyl, korzystając z następującego wzoru:
![]()
Decyl będzie zatem znajdował się w przedziale, którego częstotliwość bezwzględna jest bezpośrednio większa niż liczba uzyskana w poprzednim wyrażeniu.
A kiedy już znamy przedział, do którego należy decyl, musimy zastosować następujący wzór, aby znaleźć dokładną wartość decyla:
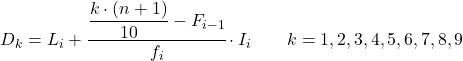
Złoto:
- L i jest dolną granicą przedziału, w którym znajduje się decyl.
- n to całkowita liczba danych statystycznych.
- F i-1 jest skumulowaną częstotliwością bezwzględną poprzedniego przedziału.
- f i jest częstotliwością bezwzględną przedziału, w którym znajduje się decyl.
- I i jest szerokością przedziału decylowego.
Abyście mogli zobaczyć jak to się robi, poniżej macie ukończone ćwiczenie, w którym obliczane są decyle 3, 5 i 8 poniższych danych pogrupowanych według przedziałów.
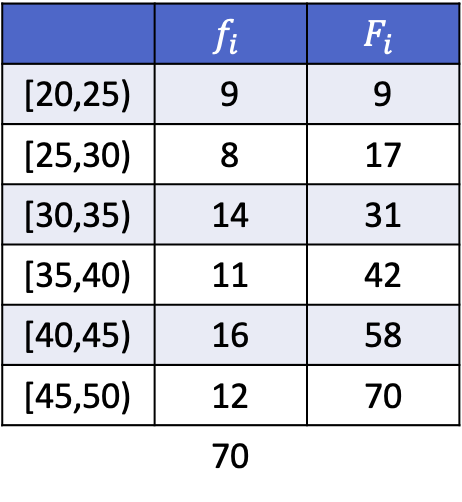
Ponieważ dane są pogrupowane, obliczenie każdego decyla składa się z dwóch etapów: najpierw należy znaleźć przedział, w którym przypada decyl, a następnie obliczyć dokładną wartość decyla. Znajdujemy zatem przedział trzeciego decyla:
![]()
![]()
Przedziałem decylowym będzie ten, którego bezwzględna skumulowana częstotliwość jest bezpośrednio większa niż 21,3 i w tym przypadku jest to przedział [30,35), którego bezwzględna skumulowana częstotliwość wynosi 31. Teraz, gdy znamy przedział decylowy, stosujemy następujący wzór, aby znaleźć dokładna wartość decyla:
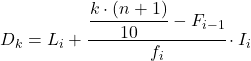
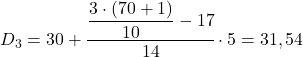
Musimy teraz ponownie zastosować metodę, aby uzyskać piąty decyl. Najpierw określamy przedział, w którym się znajduje:
![]()
Wynik 35 oznacza, że znajduje się on w przedziale [35,40), ale nie dlatego, że w wyrażeniu przedziałowym znajduje się liczba 35, ale dlatego, że jego skumulowana częstotliwość bezwzględna (42) jest bezpośrednio najwyższa. Po zidentyfikowaniu przedziału stosujemy drugą formułę procesu:
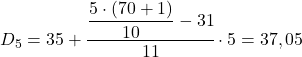
Wreszcie znajdujemy ósmy decyl. Aby to zrobić, najpierw obliczamy jego przedział:
![]()
Skumulowana częstotliwość bezwzględna bezpośrednio powyżej 56,8 wynosi 58, więc zakres ósmego decyla wynosi [40,45). Wystarczy zatem wyznaczyć dokładną wartość decyla: