Jak obliczyć dfbetas w r

W statystyce często chcemy wiedzieć, jaki wpływ mają różne obserwacje w modelach regresji.

Jednym ze sposobów obliczenia wpływu obserwacji jest użycie metryki znanej jako DFBETAS , która informuje nas o standaryzowanym wpływie na każdy współczynnik usunięcia każdej indywidualnej obserwacji.

Metryka ta daje nam wyobrażenie o wpływie każdej obserwacji na każde oszacowanie współczynnika w danym modelu regresji.

Ten samouczek pokazuje krok po kroku przykład obliczania i wizualizacji DFBETAS dla każdej obserwacji w modelu w R.

Krok 1: Utwórz model regresji

Najpierw utworzymy model regresji liniowej wielokrotnej , korzystając ze zbioru danych mtcars wbudowanego w R:

 #fit a regression model
model <- lm(mpg~disp+hp, data=mtcars)

#view model summary
summary(model)

Coefficients:
             Estimate Std. Error t value Pr(>|t|)    
(Intercept) 30.735904 1.331566 23.083 < 2nd-16 ***
available -0.030346 0.007405 -4.098 0.000306 ***
hp -0.024840 0.013385 -1.856 0.073679 .  
---
Significant. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 3.127 on 29 degrees of freedom
Multiple R-squared: 0.7482, Adjusted R-squared: 0.7309 
F-statistic: 43.09 on 2 and 29 DF, p-value: 2.062e-09

Krok 2: Oblicz DFBETAS dla każdej obserwacji

Następnie skorzystamy z wbudowanej funkcji dfbetas() do obliczenia wartości DFBETAS dla każdej obserwacji w modelu:

 #calculate DFBETAS for each observation in the model
dfbetas <- as . data . frame (dfbetas(model))

#display DFBETAS for each observation
dfbetas

                      (Intercept) disp hp
Mazda RX4 -0.1174171253 0.030760632 1.748143e-02
Mazda RX4 Wag -0.1174171253 0.030760632 1.748143e-02
Datsun 710 -0.1694989349 0.086630144 -3.332781e-05
Hornet 4 Drive 0.0577309674 0.078971334 -8.705488e-02
Hornet Sportabout -0.0204333878 0.237526523 -1.366155e-01
Valiant -0.1711908285 -0.139135639 1.829038e-01
Duster 360 -0.0312338677 -0.005356209 3.581378e-02
Merc 240D -0.0312259577 -0.010409922 2.433256e-02
Merc 230 -0.0865872595 0.016428917 2.287867e-02
Merc 280 -0.1560683502 0.078667906 -1.911180e-02
Merc 280C -0.2254489597 0.113639937 -2.760800e-02
Merc 450SE 0.0022844093 0.002966155 -2.855985e-02
Merc 450SL 0.0009062022 0.001176644 -1.132941e-02
Merc 450SLC 0.0041566755 0.005397169 -5.196706e-02
Cadillac Fleetwood 0.0388832216 -0.134511133 7.277283e-02
Lincoln Continental 0.0483781688 -0.121146607 5.326220e-02
Chrysler Imperial -0.1645266331 0.236634429 -3.917771e-02
Fiat 128 0.5720358325 -0.181104179 -1.265475e-01
Honda Civic 0.3490872162 -0.053660545 -1.326422e-01
Toyota Corolla 0.7367058819 -0.268512348 -1.342384e-01
Toyota Corona -0.2181110386 0.101336902 5.945352e-03
Dodge Challenger -0.0270169005 -0.123610713 9.441241e-02
AMC Javelin -0.0406785103 -0.141711468 1.074514e-01
Camaro Z28 0.0390139262 0.012846225 -5.031588e-02
Pontiac Firebird -0.0549059340 0.574544346 -3.689584e-01
Fiat X1-9 0.0565157245 -0.017751582 -1.262221e-02
Porsche 914-2 0.0839169111 -0.028670987 -1.240452e-02
Lotus Europa 0.3444562478 -0.402678927 2.135224e-01
Ford Pantera L -0.1598854695 -0.094184733 2.320845e-01
Ferrari Dino -0.0343997122 0.248642444 -2.344154e-01
Maserati Bora -0.3436265545 -0.511285637 7.319066e-01
Volvo 142E -0.1784974091 0.132692956 -4.433915e-02

Dla każdej obserwacji możemy zobaczyć różnicę w oszacowaniu współczynnika pochodzenia, zmiennej disp i zmiennej hp , która pojawia się po usunięciu tej konkretnej obserwacji.

Ogólnie rzecz biorąc, uważamy, że obserwacja ma duży wpływ na estymację danego współczynnika, jeśli ma wartość DBETAS większą niż próg 2/√ n , gdzie n jest liczbą obserwacji.

W tym przykładzie próg będzie wynosić 0,3535534 :

 #find number of observations
n <- nrow (mtcars)

#calculate DFBETAS threshold value
thresh <- 2/ sqrt (n)

thresh

[1] 0.3535534

Krok 3: Wizualizuj DFBETAS

Na koniec możemy utworzyć wykresy wizualizujące wartość DFBETAS dla każdej obserwacji i każdego predyktora w modelu:

 #specify 2 rows and 1 column in plotting region
by(mfrow=c(2,1))

#plot DFBETAS for disp with threshold lines
plot(dfbetas$disp, type=' h ')
abline(h = thresh, lty = 2)
abline(h = -thresh, lty = 2)

#plot DFBETAS for hp with threshold lines 
plot(dfbetas$hp, type=' h ')
abline(h = thresh, lty = 2)
abline(h = -thresh, lty = 2)

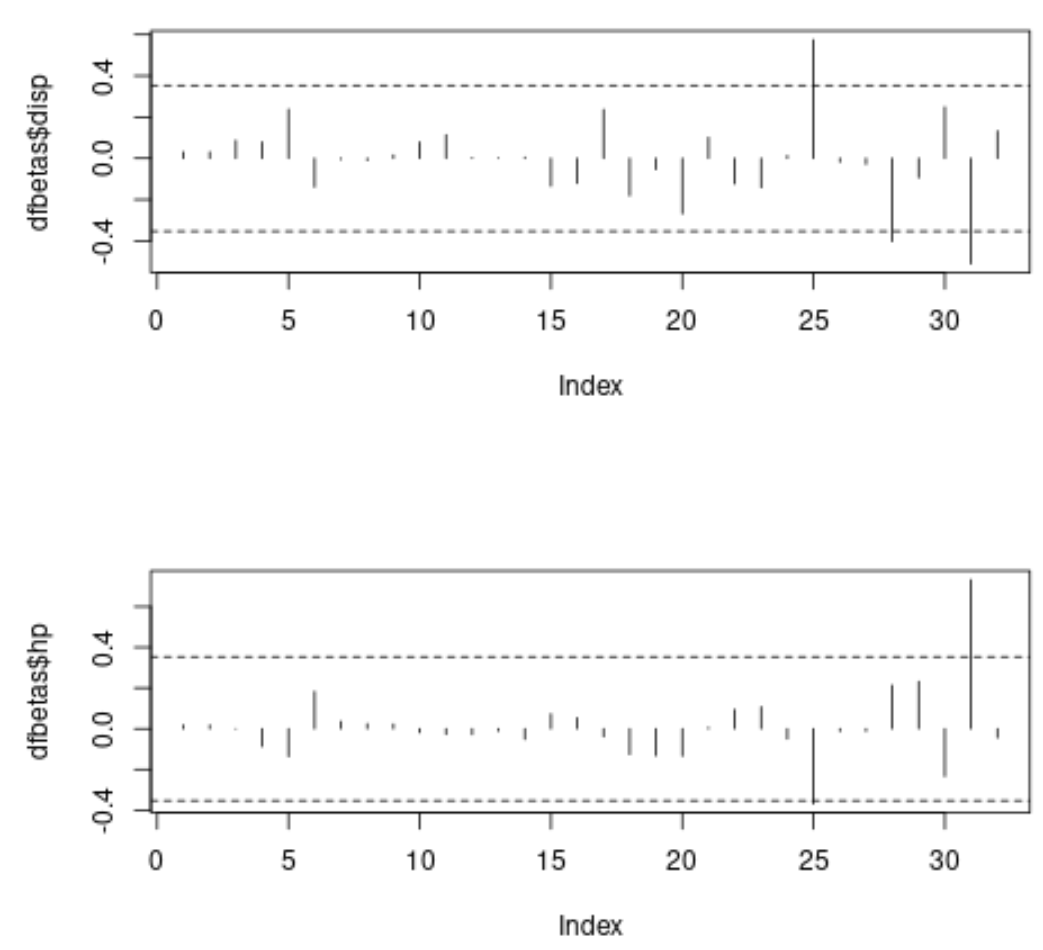
Na każdym wykresie oś x przedstawia indeks każdej obserwacji w zbiorze danych, a wartość y przedstawia odpowiednie wartości DFBETAS dla każdej obserwacji i każdego predyktora.

Na pierwszym wykresie widać, że trzy obserwacje przekraczają bezwzględną wartość progową 0,3535534 , a na drugim wykresie widać, że dwie obserwacje przekraczają bezwzględną wartość progową.

Możemy zdecydować się na dokładniejsze przestudiowanie tych obserwacji, aby ustalić, czy mają one nadmierny wpływ na estymację współczynników modelu.

Dodatkowe zasoby

Jak wykonać prostą regresję liniową w R
Jak wykonać wielokrotną regresję liniową w R
Jak obliczyć statystyki dźwigni w R
Jak obliczyć DFFITS w R