Wykresy kołowe

Przez Benjamin Anderson 5 sierpnia, 2023 Statystyka 0 komentarzy

W tym artykule wyjaśniono, czym są wykresy kołowe, jak skonstruować wykres kołowy, a ponadto będzie można zobaczyć krok po kroku ćwiczenie tego typu wykresu statystycznego.

Co to jest wykres kołowy?

Wykres kołowy lub wykres kołowy to rodzaj diagramu statystycznego, na którym dane są reprezentowane przez okrąg podzielony na sektory w taki sposób, że kąt każdego sektora jest proporcjonalny do odpowiadającej mu częstotliwości.

Innymi słowy, im wyższa częstotliwość wartości, tym większy odpowiadający jej sektor na diagramie.

Dlatego wykresy kołowe służą do wizualnej analizy częstotliwości każdej wartości. W statystyce tego typu wykresy służą głównie do przedstawiania zmiennych jakościowych.

Jak zrobić wykres kołowy

Aby utworzyć wykres kołowy, wykonaj następujące czynności:

Zbierz dane statystyczne z próbki, którą chcesz poddać analizie i utwórz tabelę częstości.
Oblicz kąt każdego sektora diagramu . Aby to zrobić, musisz użyć następującej formuły:

$\alpha_i= f_i \cdot \cfrac{360^o}{N}$

Złoto

$\alpha_i$

jest kątem sektora i ,

$f_i$

jego częstotliwość bezwzględna i

$N$

całkowita liczba danych.

Na podstawie obliczonych kątów przedstaw sektory na wykresie kołowym za pomocą kątomierza.
Oblicz procent każdego sektora na wykresie, korzystając z następującego wzoru:

$\%_i= f_i \cdot \cfrac{100}{N}$

Złoto

$\%_i$

jest procentem sektora i ,

$f_i$

jego częstotliwość bezwzględna i

$N$

całkowita liczba danych.

Wskaż na diagramie procent każdego sektora.

Przykład wykresu kołowego

Aby dokładnie zobaczyć, jak utworzyć wykres kołowy, poniżej znajduje się przykład krok po kroku:

50 osób zapytano o ulubione miasto, a dane zestawiono w poniższej tabeli. Przedstaw te dane statystyczne na wykresie kołowym.

Przede wszystkim musimy obliczyć kąt odpowiadający każdemu sektorowi, dlatego dla każdej wartości używamy następującego wzoru:

$\alpha_i = f_i \cdot \cfrac{360^o}{N}$

Złoto

$\alpha_i$

jest kątem każdego sektora,

$f_i$

jego częstotliwość i

$N$

całkowitą liczbę obserwacji.

Na przykład obliczenie kąta sektora odpowiadającego pierwszej wartości wygląda następująco:

$\alpha_{Londres}=16 \cdot \cfrac{360^o}{50} = 115,2^o$

Następnie rysujemy w okręgu sektor odpowiadający kątowi obliczonemu za pomocą kątomierza:

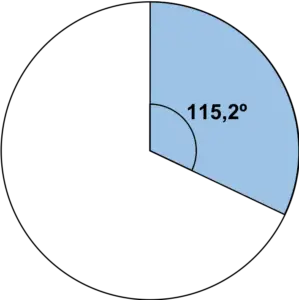
Powtarzamy tę samą procedurę dla wszystkich wartości:

$\alpha_{Paris}=12 \cdot \cfrac{360^o}{50}=86,4^o$

$\alpha_{Nueva \ York}=9\cdot \cfrac{360^o}{50}=64,8^o$

$\alpha_{Roma}= 7 \cdot \cfrac{360^o}{50} = 50,4^o$

$\alpha_{Otras}=6 \cdot \cfrac{360^o}{50} = 43,2^o$

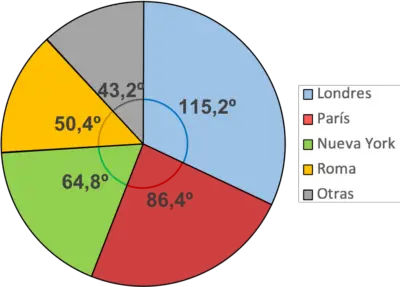
Zaleca się pomalowanie każdego sektora na inny kolor, aby ułatwić jego rozróżnienie. Podobnie należy dodać legendę wskazującą znaczenie każdego koloru.

Po przedstawieniu wszystkich sektorów konieczne jest obliczenie procentu odpowiadającego każdemu sektorowi. W tym celu stosujemy następujący wzór:

$\%_i = f_i \cdot \cfrac{100}{N}$

Złoto

$\%_i$

to procent każdego sektora,

$f_i$

jego częstotliwość i

$N$

całkowita liczba danych w badaniu statystycznym.

Procent każdego sektora wynosi zatem:

$\%_{Londres} \cdot \cfrac{100}{N}=16\cdot \cfrac{100}{50}=32\%$

$\%_{Paris}=12 \cdot \cfrac{100}{50}=24\%$

$\%_{Nueva \ York}}=9\cdot\cfrac{100}{50}=18\%$

$\%_{Roma}}=7\cdot\cfrac{100}{50}=14\%$

$\%_{Otras}=6\cdot\cfrac{100}{50}=12\%$

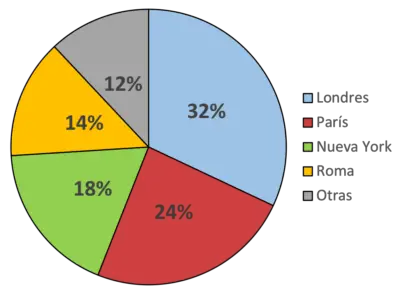
Za pomocą tego diagramu wskazujemy, że na przykład kolor niebieski reprezentuje Londyn, czyli miasto, które lubi większość ludzi (32% osób). Podobnie kolor zielony reprezentuje Nowy Jork, który jest ulubionym miastem 18% respondentów.

Zalety i wady wykresu kołowego

Wykresy kołowe ze względu na swoje cechy mają następujące zalety i wady:

Korzyść:

To bardzo wizualny wykres statystyczny, który pozwala na szybką analizę i wyciąganie wniosków.
Jest bardzo przydatny do tworzenia wykresów danych jakościowych.
Jeśli robi się to za pomocą komputera, na przykład programu Excel, można to zrobić bardzo szybko.

Niedogodności:

Kiedy na wykresie znajduje się wiele różnych sektorów, czytanie wykresu może być skomplikowane. W takim przypadku zaleca się zgrupowanie małych sektorów w jeden sektor zwany „Innymi”.
Istnieją inne typy diagramów statystycznych, które lepiej nadają się do przedstawiania zmiennych ilościowych lub szeregów czasowych.

o autorze

Dr Benjamin Anderson

Cześć, jestem Benjamin i jestem emerytowanym profesorem statystyki, który został oddanym nauczycielem Statorials. Dzięki bogatemu doświadczeniu i wiedzy specjalistycznej w dziedzinie statystyki chętnie dzielę się swoją wiedzą, aby wzmocnić pozycję uczniów za pośrednictwem Statorials. Wiedzieć więcej

Co to jest wykres kołowy?

Jak zrobić wykres kołowy

Przykład wykresu kołowego

Zalety i wady wykresu kołowego

o autorze

Dr Benjamin Anderson

Dodaj komentarz