Dlaczego statystyki są ważne? (10 powodów, dla których statystyki są ważne!)

Dziedzina statystyki zajmuje się gromadzeniem, analizą, interpretacją i prezentacją danych.

W miarę jak technologia staje się coraz bardziej obecna w naszym codziennym życiu, generuje się i gromadzi więcej danych niż kiedykolwiek wcześniej w historii ludzkości.

Statystyka to obszar, który może nam pomóc zrozumieć, w jaki sposób wykorzystywać te dane do wykonywania następujących zadań:

• Lepiej rozumieć otaczający nas świat.
• Podejmuj decyzje, korzystając z danych.
• Twórz przewidywania dotyczące przyszłości, korzystając z danych.

W tym artykule przedstawiamy 10 powodów, dla których dziedzina statystyki jest tak ważna we współczesnym życiu.

Powód 1: Używaj statystyk opisowych, aby zrozumieć świat

Statystyki opisowe służą do opisu fragmentu surowych danych. Istnieją trzy główne typy statystyk opisowych:

• Statystyki podsumowujące
• Grafika
• stoły

Każdy z tych elementów może pomóc nam lepiej zrozumieć istniejące dane.

Załóżmy na przykład, że mamy surowy zbiór danych przedstawiający wyniki testów 10 000 uczniów w określonym mieście. Statystyki opisowe możemy wykorzystywać do:

• Oblicz średni wynik testu i odchylenie standardowe wyników testu.
• Wygeneruj histogram lub wykres pudełkowy, aby zwizualizować rozkład wyników testu.
• Utwórz tabelę częstości, aby zrozumieć rozkład wyników testów.

Używając statystyk opisowych, możemy znacznie łatwiej zrozumieć wyniki testów uczniów, niż tylko patrząc na surowe dane.

Powód 2: Uważaj na wprowadzającą w błąd grafikę

Coraz więcej grafik generowanych jest w czasopismach, mediach, artykułach internetowych i magazynach. Niestety wykresy często mogą wprowadzać w błąd, jeśli nie rozumiesz danych leżących u ich podstaw.

Załóżmy na przykład, że czasopismo publikuje badanie, które wykazało ujemną korelację między wynikami GPA i ACT studentów określonej uczelni.

Jednak ta ujemna korelacja występuje tylko dlatego, że studenci, którzy mają zarówno wysoki wynik GPA, jak i ACT, mogą studiować na elitarnym uniwersytecie, podczas gdy studenci, którzy mają zarówno niski wynik GPA, jak i ACT, nie są w ogóle przyjmowani.

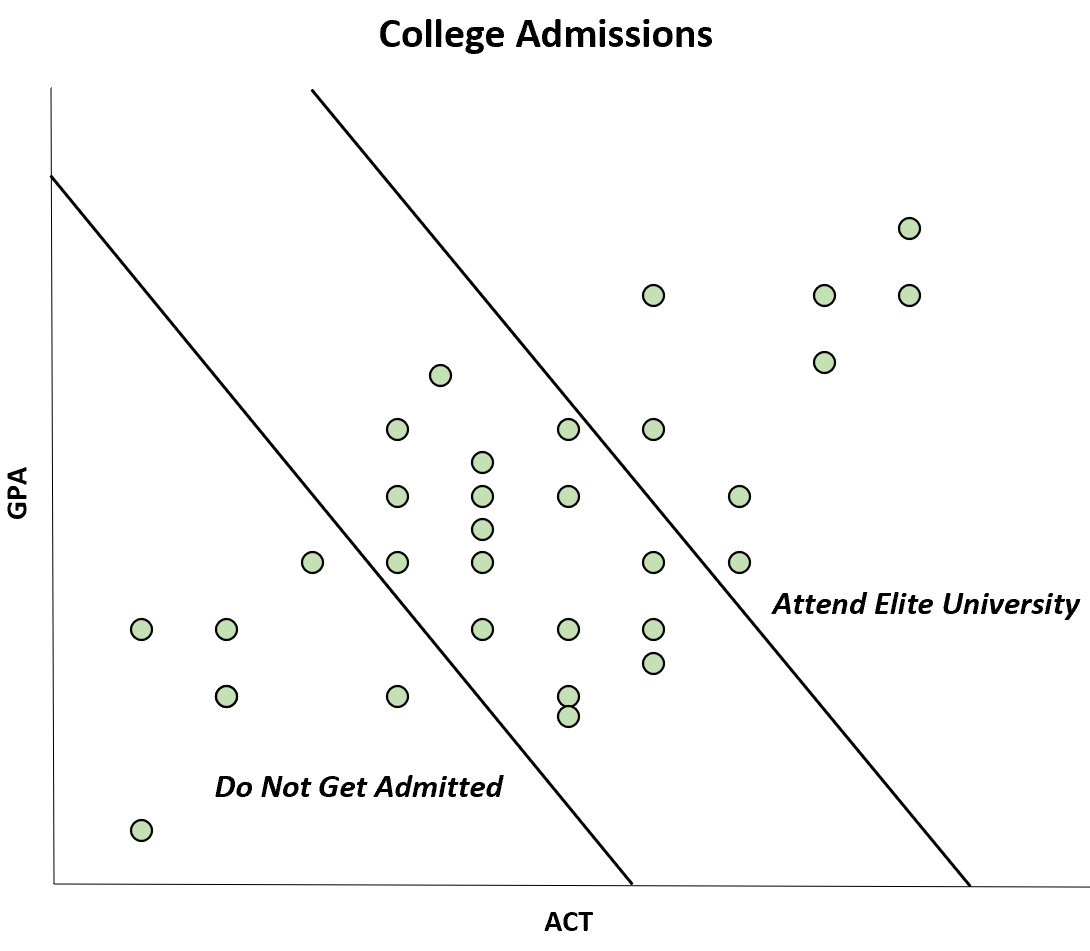
Chociaż korelacja między ACT i GPA jest w populacji dodatnia, w próbie korelacja wydaje się ujemna.

To szczególne odchylenie jest znane jako odchylenie Berksona . Mając świadomość tego błędu, możesz uniknąć wprowadzenia w błąd przez niektóre wykresy.

Powód 3: uważaj na mylące zmienne

Ważnym pojęciem, o którym dowiesz się w statystyce, jest koncepcja mylenia zmiennych .

Są to zmienne, które nie są brane pod uwagę, a mogą zafałszować wyniki eksperymentu i prowadzić do nierzetelnych wniosków.

Załóżmy na przykład, że badacz zbiera dane dotyczące sprzedaży lodów i ataków rekinów i odkrywa, że te dwie zmienne są silnie skorelowane. Czy to oznacza, że zwiększona sprzedaż lodów powoduje więcej ataków rekinów?

Jest mało prawdopodobne. Najbardziej prawdopodobną przyczyną jest myląca zmienna temperatura . Kiedy na zewnątrz jest cieplej, więcej osób kupuje lody i więcej osób wybiera się nad ocean.

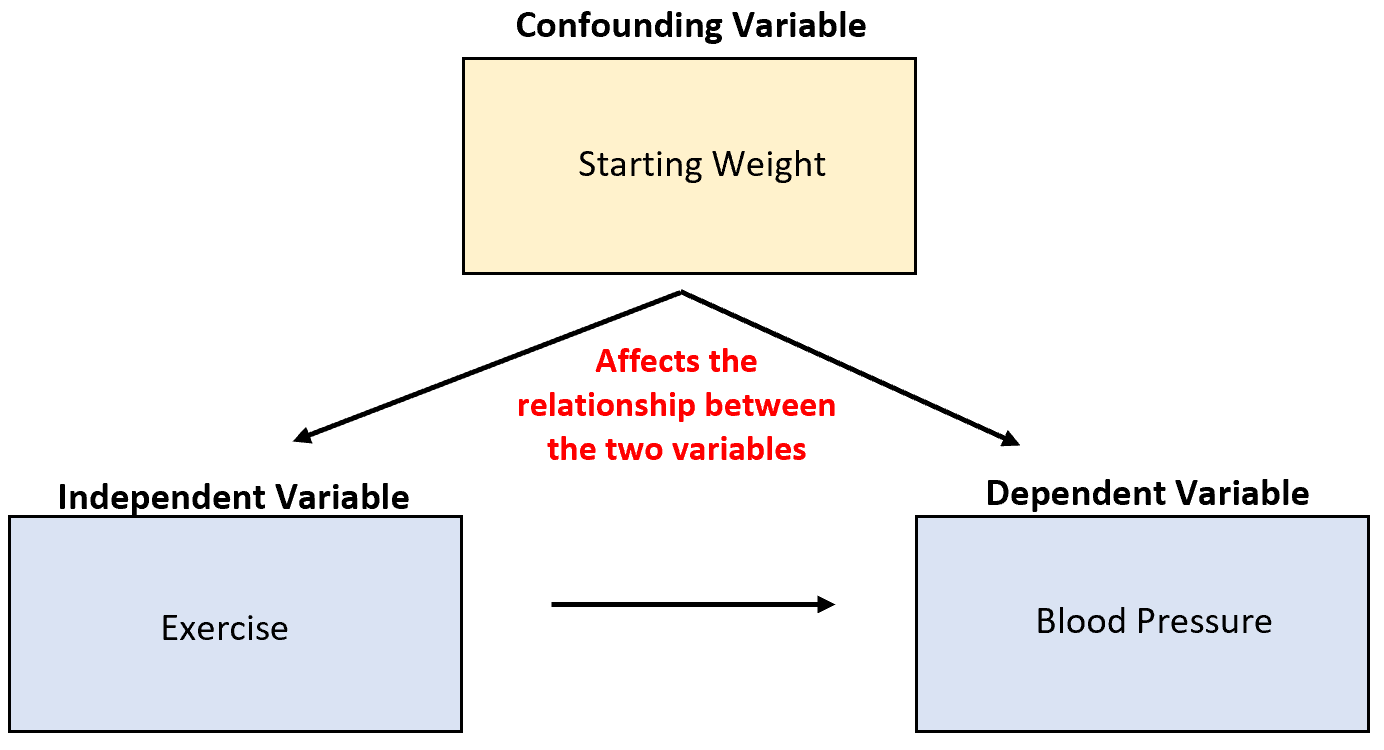
Powód 4: podejmować lepsze decyzje na podstawie prawdopodobieństwa

Jednym z najważniejszych poddziedzin statystyki jest prawdopodobieństwo . Jest to dziedzina badająca prawdopodobieństwo wystąpienia zdarzeń.

Mając podstawową wiedzę na temat prawdopodobieństwa, możesz podejmować bardziej świadome decyzje w prawdziwym świecie.

Załóżmy na przykład, że licealista wie, że ma 10% szans na przyjęcie na daną uczelnię. Korzystając ze wzoru na prawdopodobieństwo zaliczenia „co najmniej jednej” , student ten może obliczyć prawdopodobieństwo, że zostanie przyjęty na co najmniej jedną uczelnię, na którą aplikuje, oraz może dostosować liczbę uczelni, na które aplikuje, według wyniku.

Powód 5: Zrozumienie wartości P w badaniach

Innym ważnym pojęciem, o którym dowiesz się w statystyce, są wartości p .

Klasyczna definicja wartości p to:

Wartość p to prawdopodobieństwo zaobserwowania statystyki próbki, która jest co najmniej tak ekstremalna jak statystyka próbki, przy założeniu, że hipoteza zerowa jest prawdziwa.

Załóżmy na przykład, że fabryka twierdzi, że produkuje opony o średniej masie 200 funtów. Audytor stawia hipotezę, że rzeczywista średnia waga opon produkowanych w tym zakładzie różni się o 200 funtów. Przeprowadza więc test hipotezy i stwierdza, że wartość p testu wynosi 0,04.

Oto jak interpretować tę wartość p:

Jeśli fabryka rzeczywiście produkuje opony o średniej wadze 200 funtów, to w 4% wszystkich audytów uzyskamy efekt zaobserwowany w próbce lub więcej, ze względu na błąd losowej próby. To mówi nam, że uzyskanie przykładowych danych uzyskanych przez audytora byłoby dość rzadkie, gdyby fabryka faktycznie produkowała opony o średniej wadze 200 funtów.

W związku z tym audytor prawdopodobnie odrzuciłby hipotezę zerową, zgodnie z którą rzeczywista średnia waga opon produkowanych w tym zakładzie w rzeczywistości wynosi 200 funtów.

Powód 6: Zrozum korelację

Innym ważnym pojęciem, o którym dowiesz się w statystyce, jest korelacja , która mówi nam o liniowym powiązaniu między dwiema zmiennymi.

Wartość współczynnika korelacji zawsze mieści się w przedziale od -1 do 1, gdzie:

• -1 oznacza całkowicie ujemną korelację liniową pomiędzy dwiema zmiennymi
• Wartość 0 oznacza brak liniowej korelacji pomiędzy dwiema zmiennymi
• 1 wskazuje doskonale dodatnią korelację liniową pomiędzy dwiema zmiennymi

Rozumiejąc te wartości, można zrozumieć związek między zmiennymi w świecie rzeczywistym.

Na przykład, jeśli korelacja między wydatkami na reklamę a przychodami wynosi 0,87, można zrozumieć, że istnieje silny pozytywny związek między tymi dwiema zmiennymi. Kiedy wydajesz więcej pieniędzy na reklamę, możesz spodziewać się przewidywalnego wzrostu przychodów.

Powód 7: Przewiduj przyszłość

Innym ważnym powodem uczenia się statystyki jest zrozumienie podstawowych modeli regresji, takich jak:

• Prosta regresja liniowa
• Wielokrotna regresja liniowa
• Regresja logistyczna

Każdy z tych modeli umożliwia przewidywanie przyszłej wartościzmiennej odpowiedzi na podstawie wartości określonych zmiennych predykcyjnych w modelu.

Na przykład firmy cały czas korzystają z wielu modeli regresji liniowej w świecie rzeczywistym, korzystając ze zmiennych predykcyjnych, takich jak wiek, dochód, pochodzenie etniczne itp. aby przewidzieć, ile klientów wyda w ich sklepach.

Podobnie firmy logistyczne wykorzystują zmienne predykcyjne, takie jak całkowity popyt, wielkość populacji itp. prognozować przyszłą sprzedaż.

Bez względu na dziedzinę, w której pracujesz, istnieje duża szansa, że modele regresji zostaną wykorzystane do przewidzenia przyszłego zjawiska.

Powód 8: Zrozumienie potencjalnej stronniczości w badaniach

Innym powodem studiowania statystyki jest świadomość różnych rodzajów uprzedzeń, które mogą pojawić się w badaniach w świecie rzeczywistym.

Oto kilka przykładów:

• Obserwuj stronniczość
• Błędy autoselekcji
• Stronniczość odniesienia
• Pominięte zmienne odchylenie
• Niedoszacowanie
• Stronniczość braku odpowiedzi

Mając podstawową wiedzę na temat tego typu uprzedzeń, możesz uniknąć ich popełniania podczas prowadzenia badań lub mieć ich świadomość podczas czytania innych artykułów naukowych lub badań.

Powód 9: Zrozum założenia przyjęte na podstawie testów statystycznych

Wiele testów statystycznych przyjmuje założenia dotyczące badanych danych.

Czytając wyniki badania lub nawet przeprowadzając własne badanie, ważne jest, aby zrozumieć, jakie założenia należy przyjąć, aby wyniki były wiarygodne.

W poniższych artykułach przedstawiono założenia przyjęte w wielu powszechnie stosowanych testach i procedurach statystycznych:

• Jakie jest założenie o równej wariancji w statystyce?
• Jakie jest założenie normalności w statystyce?
• Jakie jest założenie niezależności w statystyce?

Powód 10: Aby uniknąć nadmiernego uogólnienia

Innym powodem studiowania statystyki jest zrozumienie koncepcji nadmiernej generalizacji .

Dzieje się tak, gdy osoby biorące udział w badaniu nie są reprezentatywne dla osób w całej populacji i dlatego niewłaściwe jest uogólnianie wyników badania na całą populację.

Załóżmy na przykład, że chcemy wiedzieć, jaki procent uczniów w określonej szkole preferuje „dramat” jako swój ulubiony gatunek filmowy. Jeżeli całkowita populacja uczniów składa się z 50% chłopców i 50% dziewcząt, wówczas próba składająca się z 90% chłopców i 10% dziewcząt może prowadzić do stronniczych wyników, jeśli znacznie mniej chłopców preferuje teatr jako swój ulubiony gatunek.

Idealnie byłoby, gdyby nasza próba przypominała „mini wersję” naszej populacji. Zatem jeśli ogólna populacja uczniów składa się z 50% dziewcząt i 50% chłopców, nasza próba nie byłaby reprezentatywna, gdyby obejmowała 90% chłopców i tylko 10% dziewcząt.

Zatem niezależnie od tego, czy przeprowadzasz własną ankietę, czy czytasz wyniki ankiety, ważne jest, aby zrozumieć, czy dane z próby są reprezentatywne dla całej populacji i czy wyniki ankiety można z pewnością uogólnić na populację.

Dodatkowe zasoby

Zapoznaj się z poniższymi artykułami, aby uzyskać podstawową wiedzę na temat najważniejszych pojęć we wprowadzających statystykach:

Statystyki opisowe lub wnioskowane
Populacja vs. próbka
Statystyki a parametry
Zmienne jakościowe i ilościowe
Poziomy pomiaru: nominalny, porządkowy, interwałowy i ilorazowy