Co uważa się za dobrą, a co złą fabułę rezydualną?

W analizie regresji wykres reszt jest rodzajem wykresu, który wyświetla dopasowane wartości modelu regresji na osi x i reszty modelu wzdłuż osi y.

Podczas wizualnej kontroli pozostałego układu zazwyczaj szukamy dwóch rzeczy, aby określić, czy układ jest „dobry”, czy „zły”:

1. Czy reszty wykazują wyraźny trend?

• Na „dobrym” wykresie reszt reszty nie wykazują wyraźnego trendu.
• Na „złym” wykresie reszt reszty mają pewien wzór, taki jak krzywa lub fala. Oznacza to, że zastosowany przez nas model regresji nie zapewnia odpowiedniego dopasowania do danych.

2. Czy reszty wariancji systematycznie zwiększają się czy zmniejszają?

• Na „dobrym” wykresie reszt reszty są losowo rozrzucone wokół zera bez systematycznego wzrostu lub spadku wariancji.
• Na „złym” wykresie reszt wariancja reszt systematycznie rośnie lub maleje.

Jeżeli wykres resztowy zostanie oceniony jako „dobry”, oznacza to, że możemy ufać wynikom modelu regresji i że można bezpiecznie interpretować współczynniki modelu.

Jeśli jednak wykres reszt zostanie oceniony jako „zły”, oznacza to, że wyniki modelu są niewiarygodne i musimy dopasować do danych inny model regresji.

Poniższe przykłady wyjaśniają, jak w praktyce interpretować „dobre” i „złe” wykresy resztowe.

Przykład 1: „dobry” ślad resztkowy

Załóżmy, że dopasowujemy model regresji i otrzymujemy następujący wykres reszt:

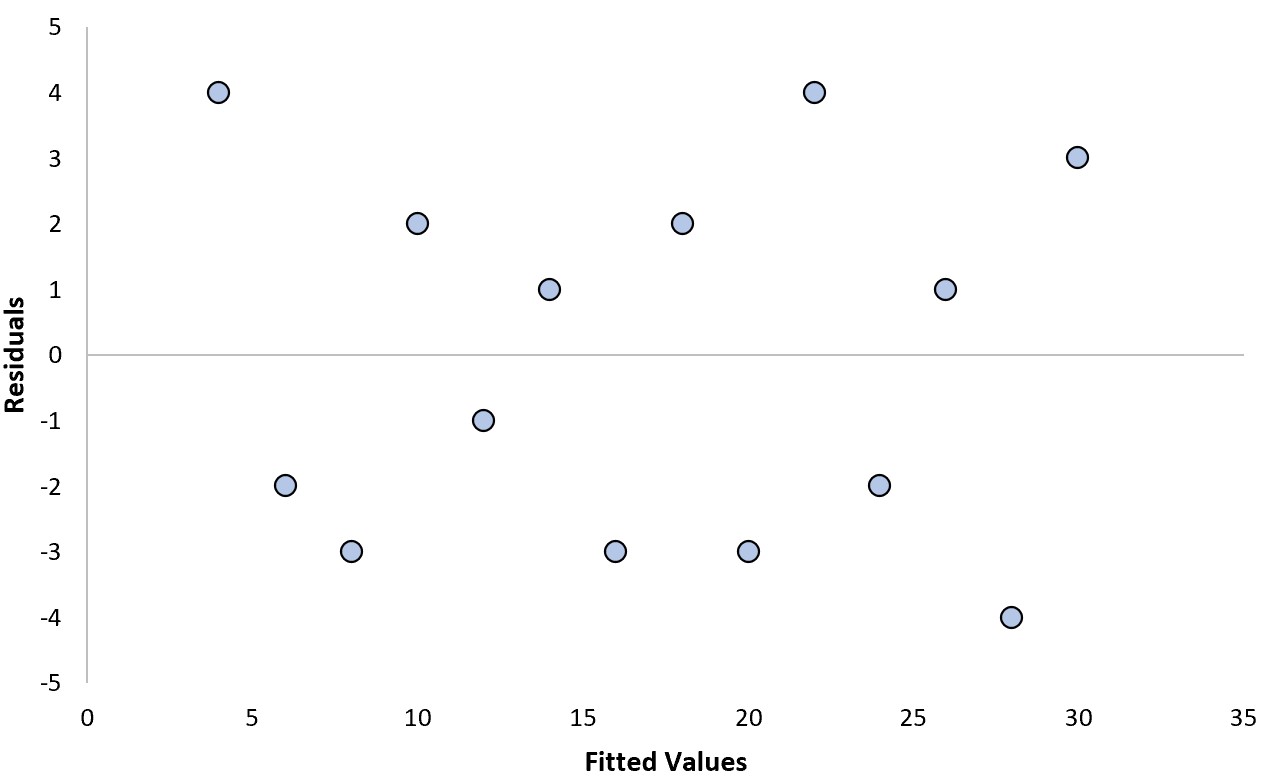
Aby określić, czy jest to „dobry” wykres resztowy, możemy odpowiedzieć na następujące dwa pytania:

1. Czy reszty wykazują wyraźny trend?

Nie. Reszty są losowo rozproszone wokół zera, bez wyraźnego wzoru.

2. Czy reszty wariancji systematycznie zwiększają się czy zmniejszają?

Nie. Reszty mają dość stałą wariancję (tj. odległość między resztami a wartością zerową) na każdym poziomie dopasowanych wartości.

Ponieważ odpowiedzieliśmy „Nie” na oba te pytania, uznalibyśmy to za „dobry” wątek resztkowy.

Można zatem ufać wynikom modelu regresji i bezpiecznie interpretować współczynniki modelu.

Przykład 2: „zły” wykres resztowy z przejrzystym modelem

Załóżmy, że dopasowujemy model regresji i otrzymujemy następujący wykres reszt:

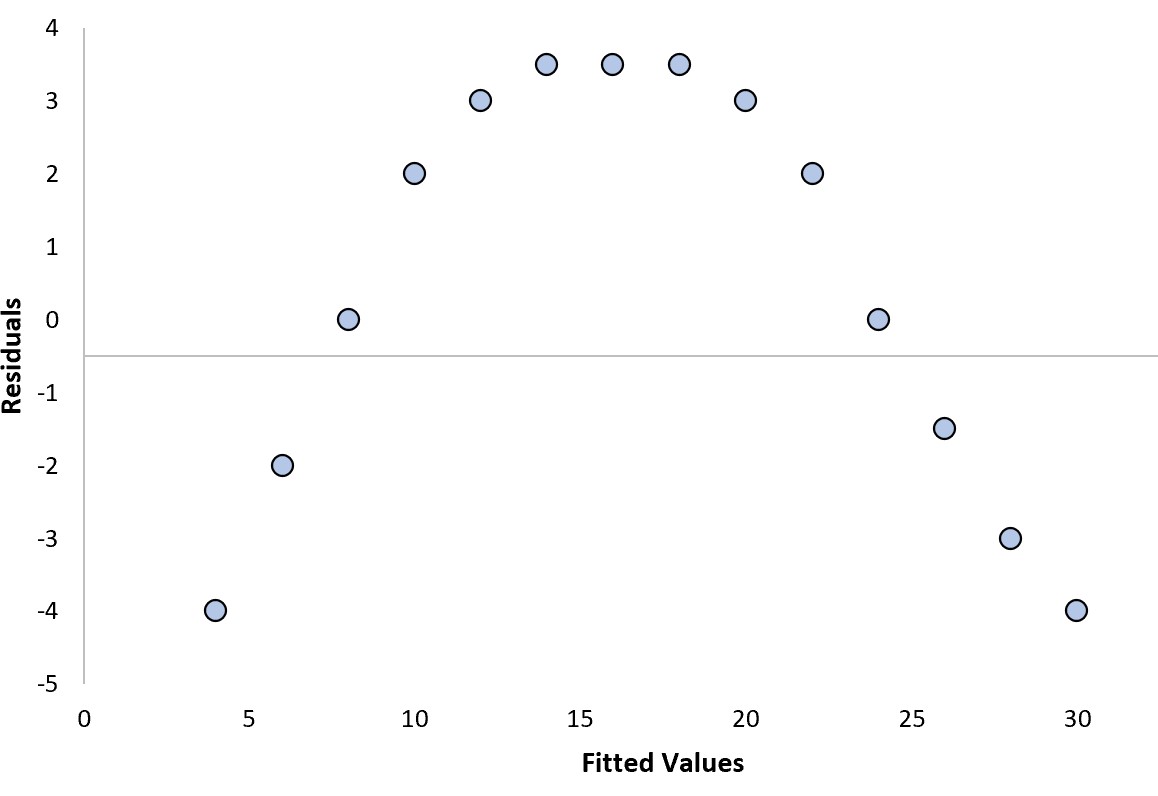
Aby określić, czy jest to „dobry” wykres resztowy, możemy odpowiedzieć na następujące dwa pytania:

1. Czy reszty wykazują wyraźny trend?

Tak . Pozostałości mają zakrzywiony wzór.

2. Czy reszty wariancji systematycznie zwiększają się czy zmniejszają?

Tak . Reszty mają różne poziomy wariancji na różnych poziomach dopasowanych wartości.

Ponieważ odpowiedzieliśmy „Tak” na co najmniej jedno z tych pytań, uznalibyśmy to za „zły” wątek resztkowy.

Oznacza to, że model regresji nie zapewnia dobrego dopasowania do danych.

W szczególności zakrzywiony wzór na wykresie reszt wskazuje, że model regresji liniowej nie pasuje do danych i że model regresji kwadratowej prawdopodobnie sprawdziłby się lepiej.

Przykład 3: „zły” wykres reszt o rosnącej wariancji

Załóżmy, że dopasowujemy model regresji i otrzymujemy następujący wykres reszt:

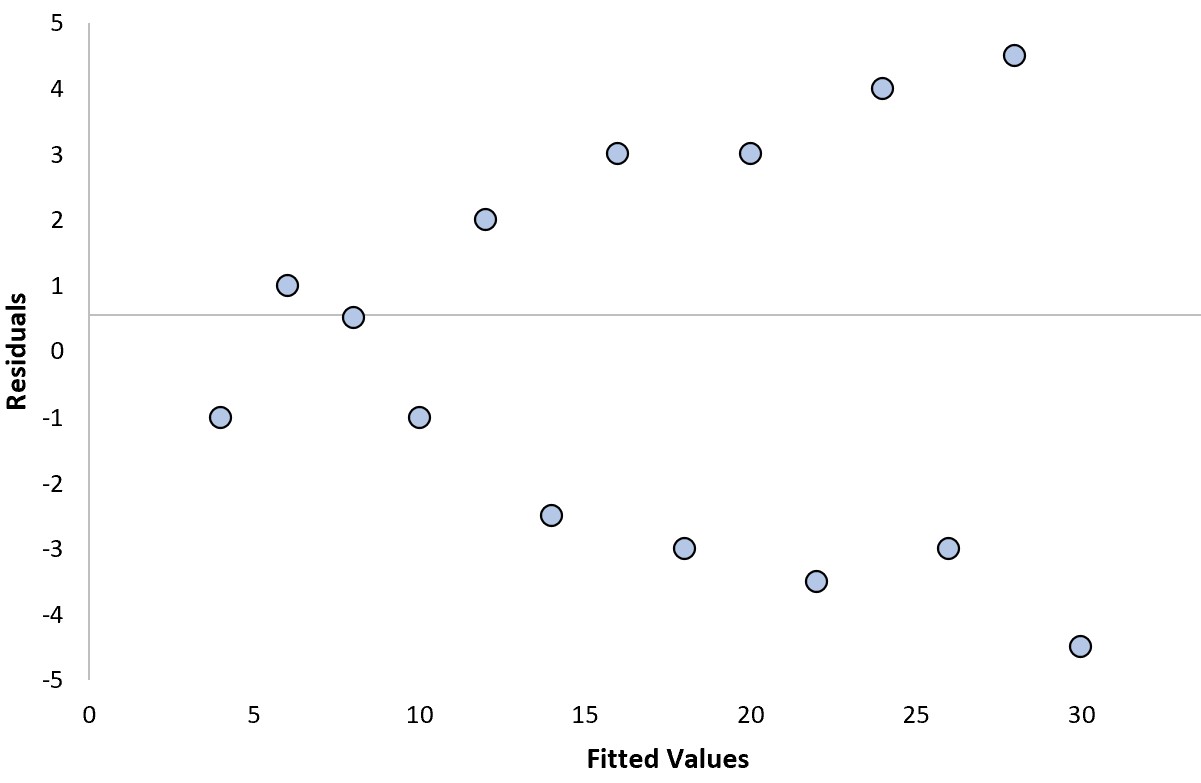
Aby określić, czy jest to „dobry” wykres resztowy, możemy odpowiedzieć na następujące dwa pytania:

1. Czy reszty wykazują wyraźny trend?

Nie. Nie ma wyraźnego trendu w zakresie reszt.

2. Czy reszty wariancji systematycznie zwiększają się czy zmniejszają?

Tak . Wariancja reszt wzrasta wraz ze wzrostem dopasowanych wartości.

Ponieważ odpowiedzieliśmy „Tak” na co najmniej jedno z tych pytań, uznalibyśmy to za „zły” wątek resztkowy.

W tym konkretnym przykładzie reszty cierpią na heteroskedastyczność , która odnosi się do nierównej wariancji reszt na różnych poziomach dopasowanych wartości.

Oznacza to, że wyniki modelu regresji mogą nie być wiarygodne.

Zapoznaj się z tym artykułem , aby poznać różne sposoby rozwiązania problemu heteroskedastyczności w modelu regresji.

Dodatkowe zasoby

Poniższe samouczki wyjaśniają, jak tworzyć wykresy reszt przy użyciu różnych programów statystycznych:

Jak utworzyć wykres rezydualny w R
Jak utworzyć wykres resztkowy w Pythonie
Jak utworzyć wykres resztowy w programie Excel
Jak utworzyć działkę resztkową w SAS-ie