Jak wykonać dokładny test fishera w sas
Dokładny test Fishera służy do określenia, czy istnieje istotny związek między dwiema zmiennymi kategorycznymi.
Jest powszechnie stosowany jako alternatywa dla testu niezależności chi-kwadrat, gdy liczba co najmniej jednej komórki w tabeli 2 × 2 jest mniejsza niż 5.
Dokładny test Fishera wykorzystuje następujące hipotezy zerowe i alternatywne:
- H 0 : (hipoteza zerowa) Te dwie zmienne są niezależne.
- H 1 : (hipoteza alternatywna) Te dwie zmienne nie są niezależne.
Jeśli wartość p testu jest mniejsza niż pewien poziom istotności, możemy odrzucić hipotezę zerową testu i stwierdzić, że te dwie zmienne nie są niezależne, to znaczy mają istotny związek.
Poniższy przykład pokazuje, jak przeprowadzić dokładny test Fishera w SAS-ie.
Przykład: dokładny test Fishera w SAS
Załóżmy, że chcemy wiedzieć, czy płeć jest powiązana z preferencją partii politycznej na określonej uczelni.
Aby to zbadać, losowo wybieramy 25 studentów w kampusie i pytamy ich o preferencje dotyczące partii politycznych. Wyniki przedstawiono w poniższej tabeli:
| Demokrata | Republikański | |
|---|---|---|
| Kobieta | 8 | 4 |
| Mężczyzna | 4 | 9 |
Aby określić, czy istnieje statystycznie istotny związek między płcią a preferencjami partii politycznych, możemy wykonać następujące kroki w celu przeprowadzenia dokładnego testu Fishera w SAS:
Krok 1: Utwórz dane
Najpierw utwórzmy zbiór danych o nazwie my_data :
/*create data to hold survey results*/ data my_data; input Party$Gender$; datalines ; Rep Female Rep Female Rep Female Rep Female Rep Male Rep Male Rep Male Rep Male Rep Male Rep Male Rep Male Rep Male Rep Male Dem Female Dem Female Dem Female Dem Female Dem Female Dem Female Dem Female Dem Female Dem Male Dem Male Dem Male Dem Male ; run ;
Krok 2: Wykonaj dokładny test Fishera
Następnie możemy użyć następującego kodu, aby przeprowadzić dokładny test Fishera:
/*perform Fisher's Exact test*/ proc freq ; Party*Gender / fisher tables ; run ;
Wyniki testu przedstawiono poniżej:
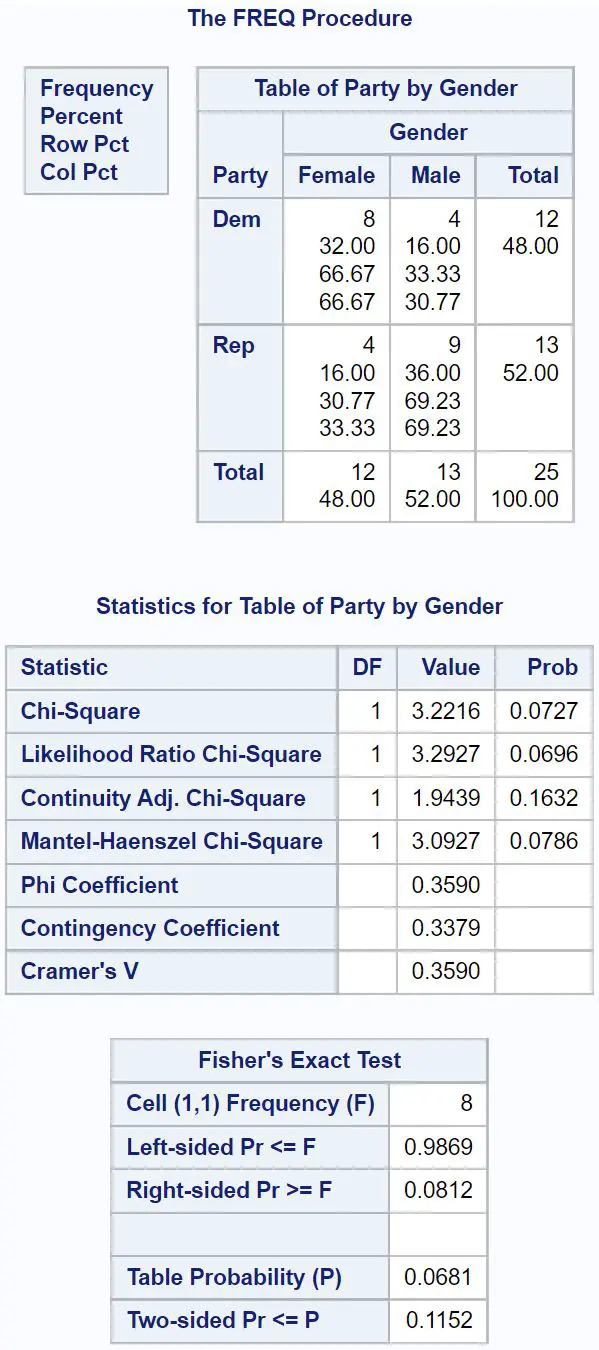
Hipotezą zerową dokładnego testu Fishera jest to, że obie zmienne są niezależne. W tym przykładzie naszą hipotezą zerową jest to, że preferencje dotyczące płci i partii politycznych są niezależne, co jest testem dwustronnym.
Przyjrzymy się zatem dwustronnej wartości p w tabeli wyników końcowych, która okazuje się wynosić 0,1152 .
Ponieważ ta wartość p jest nie mniejsza niż 0,05, nie odrzucamy hipotezy zerowej.
Oznacza to, że nie mamy wystarczających dowodów, aby stwierdzić, że istnieje istotny związek między płcią a preferencjami partii politycznych.
Dodatkowe zasoby
Poniższe samouczki zawierają dodatkowe informacje na temat dokładnego testu Fishera:
Wprowadzenie do dokładnego testu Fishera
Kalkulator testu dokładnego Fishera
Jak zgłaszać dokładne wyniki testu Fishera