Jak przeprowadzić dokładny test fishera w spss
Dokładny test Fishera służy do określenia, czy istnieje istotny związek między dwiema zmiennymi kategorycznymi.
Jest powszechnie stosowany jako alternatywa dla testu niezależności chi-kwadrat, gdy liczba co najmniej jednej komórki w tabeli 2 × 2 jest mniejsza niż 5.
W tym samouczku wyjaśniono, jak przeprowadzić dokładny test Fishera w SPSS.
Przykład: dokładny test Fishera w SPSS
Załóżmy, że chcemy wiedzieć, czy płeć jest powiązana z preferencją partii politycznej na określonej uczelni. Aby to zbadać, przeprowadziliśmy losową ankietę wśród 25 studentów na terenie kampusu. Liczbę studentów Demokratów i Republikanów, w zależności od płci, przedstawiono w poniższej tabeli:
| Demokrata | Republikański | |
|---|---|---|
| Kobieta | 8 | 4 |
| Mężczyzna | 4 | 9 |
Aby określić, czy istnieje statystycznie istotny związek między płcią a preferencjami partii politycznych, możemy wykonać następujący dokładny test Fishera w SPSS:
Krok 1: Wprowadź dane.
Najpierw wprowadź dane jak pokazano poniżej:
W każdym wierszu wyświetlany jest identyfikator danej osoby, preferencje partii politycznej i płeć.
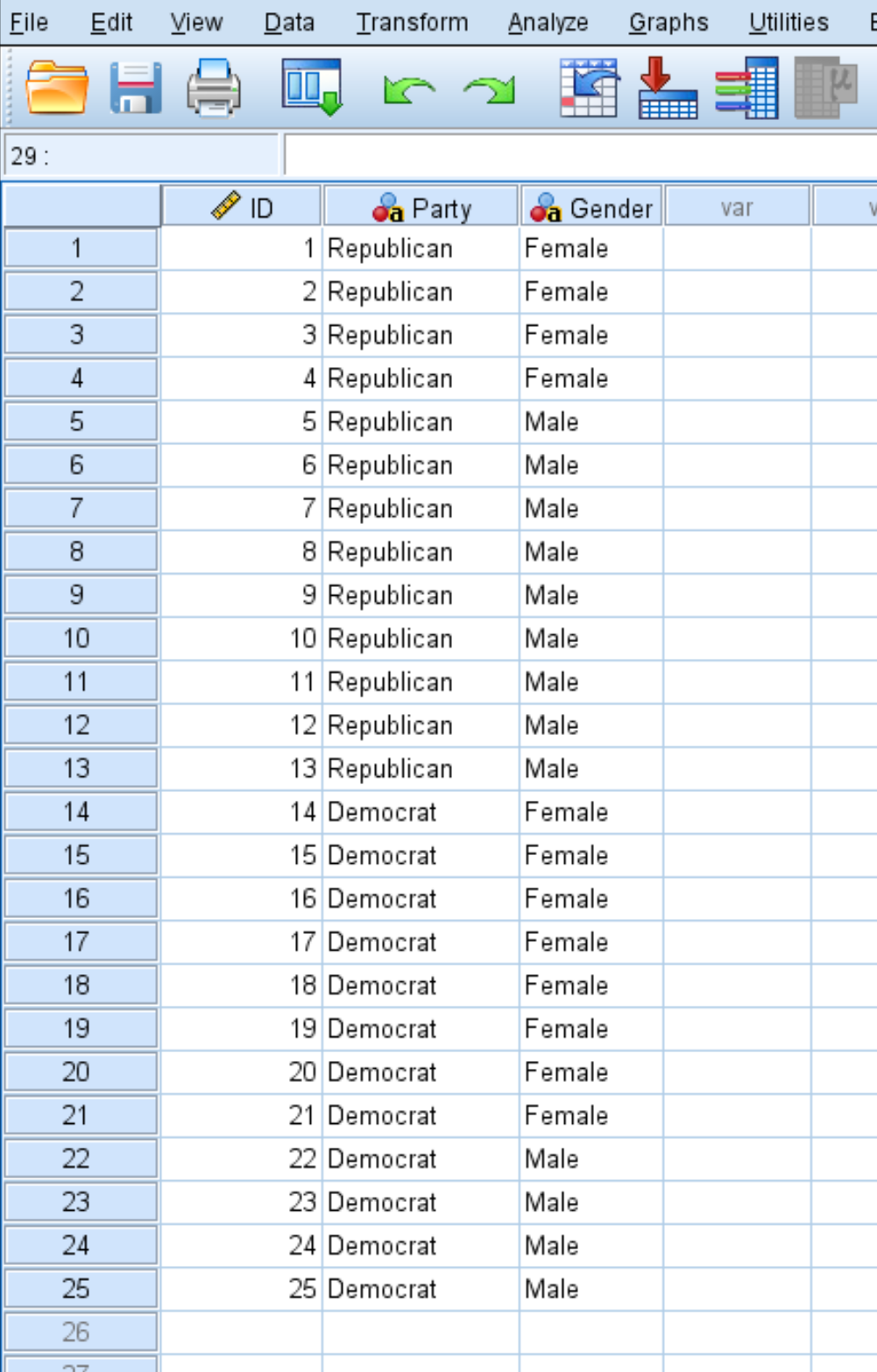
Krok 2: Wykonaj dokładny test Fishera.
Kliknij kartę Analiza , następnie Statystyki opisowe i Tabele przestawne :
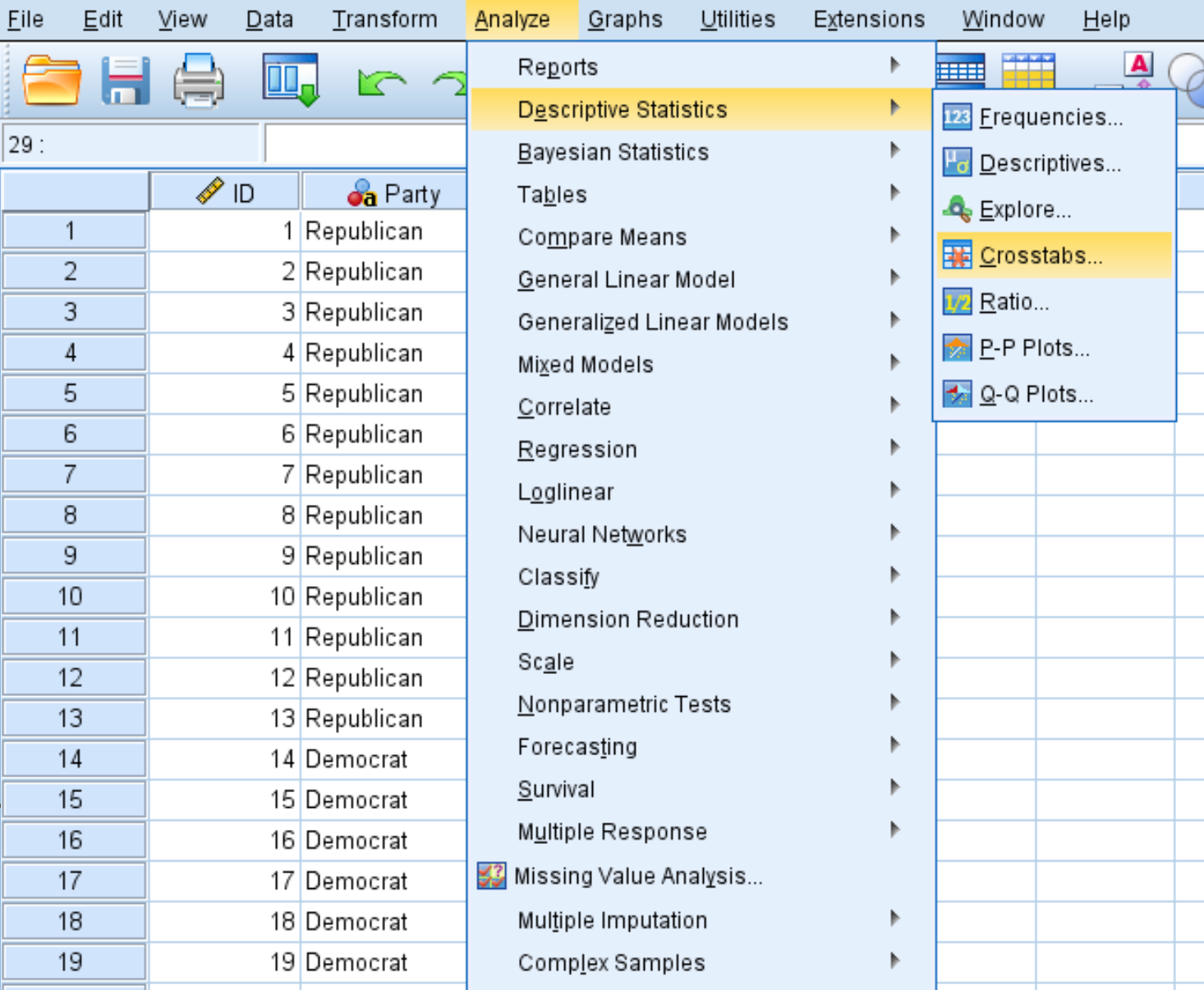
Przeciągnij zmienną Płeć do obszaru o nazwie Wiersze, a zmienną Część do obszaru o nazwie Kolumny. Następnie kliknij przycisk Statystyki i upewnij się, że pole obok Chi Square jest zaznaczone. Następnie kliknij Kontynuuj .
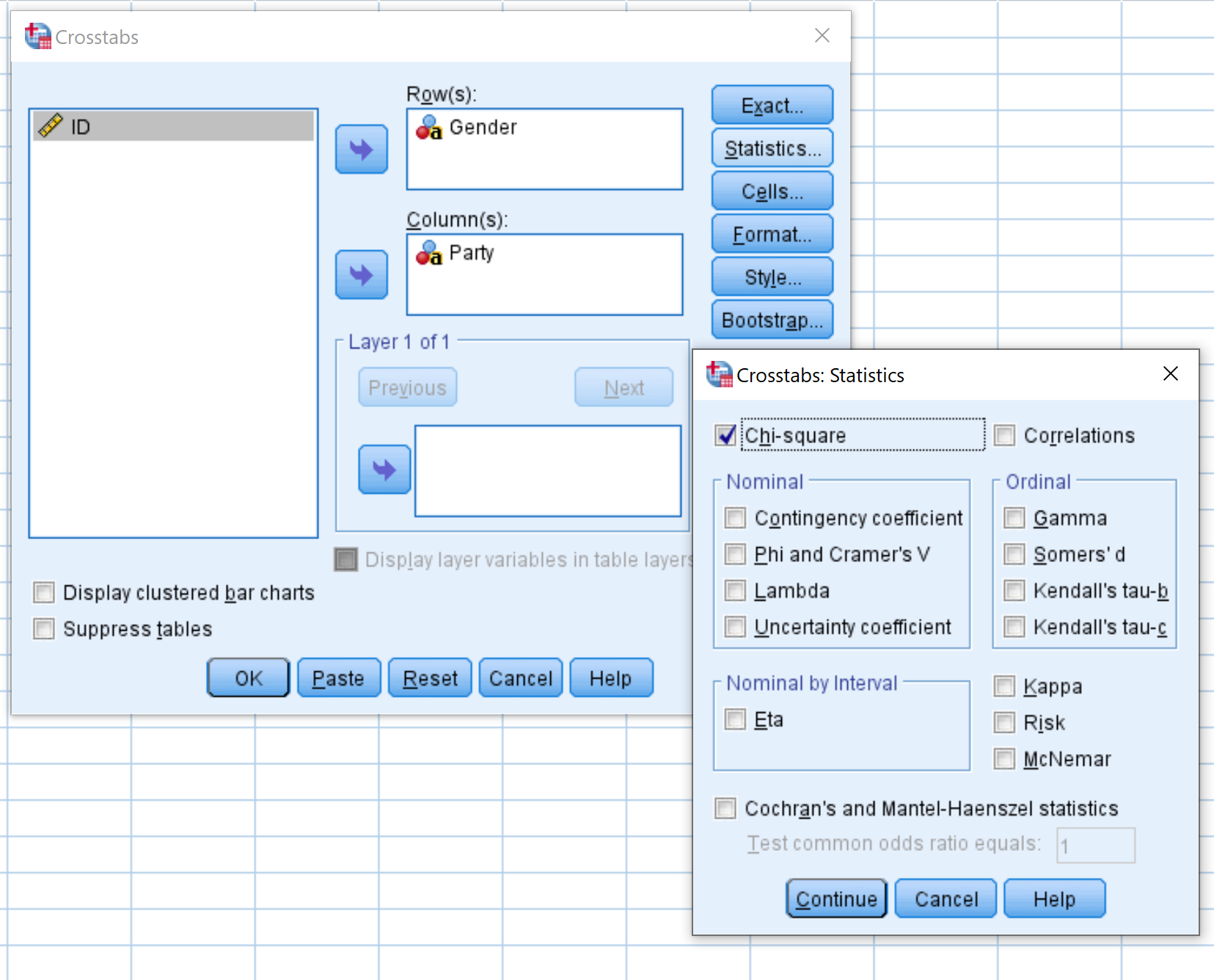
Następnie kliknij przycisk Dokładny i upewnij się, że pole obok Dokładne jest zaznaczone. Następnie kliknij Kontynuuj .
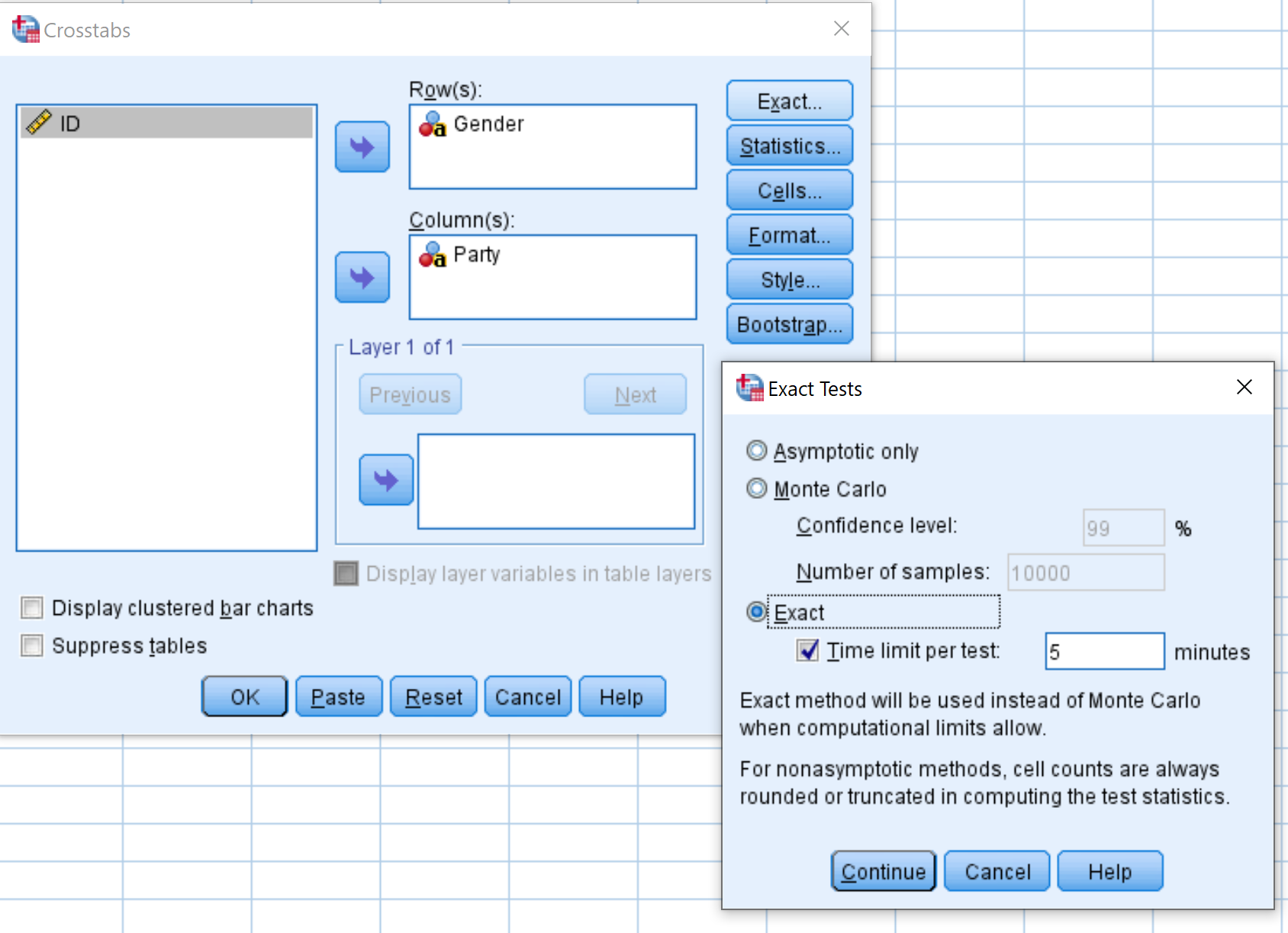
Na koniec kliknij OK , aby przeprowadzić dokładny test Fishera.
Krok 3: Interpretacja wyników.
Po kliknięciu OK wyświetlą się wyniki dokładnego testu Fishera:
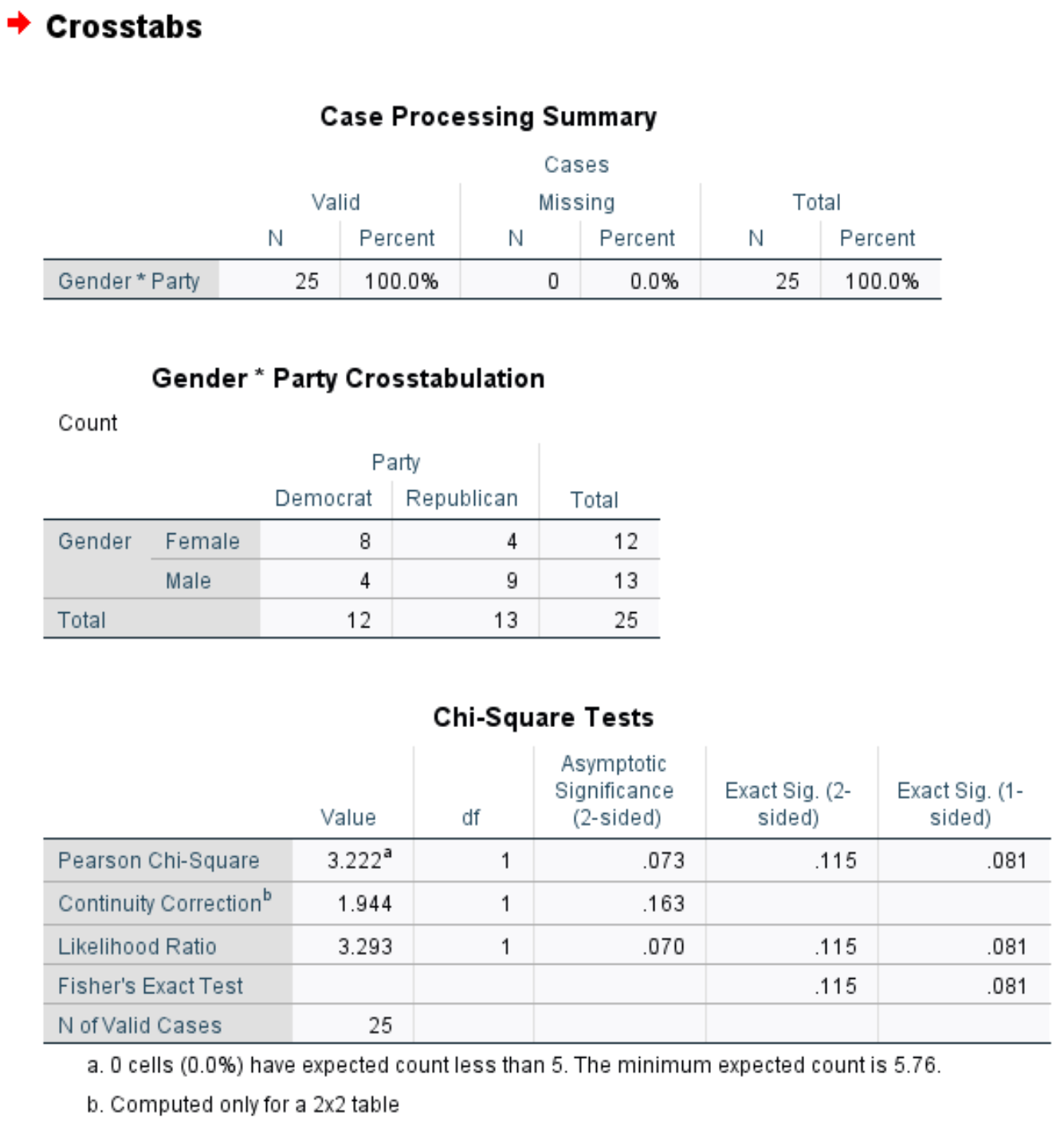
Pierwsza tabela wyświetla liczbę brakujących obserwacji w zbiorze danych. Widzimy, że w tym przykładzie brakuje 0 przypadków.
Druga tabela przedstawia tabelę krzyżową całkowitej liczby osób według płci i preferencji partii politycznych.
Trzecia tabela przedstawia wyniki dokładnego testu Fishera. W teście możemy zobaczyć następujące dwie wartości p:
- Dwustronna wartość p: 0,115
- Jednostronna wartość p: 0,081
Hipotezą zerową dokładnego testu Fishera jest to, że obie zmienne są niezależne. W tym przypadku nasza hipoteza zerowa głosi, że płeć i preferencje dotyczące partii politycznych są niezależne, co jest testem dwustronnym, zatem użylibyśmy dwustronnej wartości p wynoszącej 0,115.
Ponieważ ta wartość p jest nie mniejsza niż 0,05, nie odrzucamy hipotezy zerowej. Nie mamy zatem wystarczających dowodów, aby stwierdzić, że istnieje znaczący związek między płcią a preferencjami dotyczącymi partii politycznych.