Jak wykonać dokładny test fishera w stata
Dokładny test Fishera służy do określenia, czy istnieje istotny związek między dwiema zmiennymi kategorycznymi. Jest powszechnie stosowany jako alternatywa dla testu niezależności chi-kwadrat, gdy liczba co najmniej jednej komórki w tabeli 2 × 2 jest mniejsza niż 5.
W tym samouczku wyjaśniono, jak przeprowadzić dokładny test Fishera w programie Stata.
Przykład: dokładny test Fishera w Stata
Załóżmy, że chcemy wiedzieć, czy płeć jest powiązana z preferencją partii politycznej na określonej uczelni. Aby to zbadać, przeprowadziliśmy losową ankietę wśród 25 studentów na terenie kampusu. Liczbę studentów Demokratów i Republikanów, w zależności od płci, przedstawiono w poniższej tabeli:
| Demokrata | Republikański | |
|---|---|---|
| Mężczyzna | 4 | 9 |
| Kobieta | 8 | 4 |
Aby określić, czy istnieje statystycznie istotny związek między płcią a preferencjami partii politycznych, możemy przeprowadzić dokładny test Fishera.
W Stata możemy użyć polecenia tabi , aby wykonać dokładny test Fishera. Liczby wprowadzamy w tabeli 2×2 od lewej do prawej, używając znaku \ , aby oddzielić górny i dolny wiersz.
tabi 4 9 \ 8 4
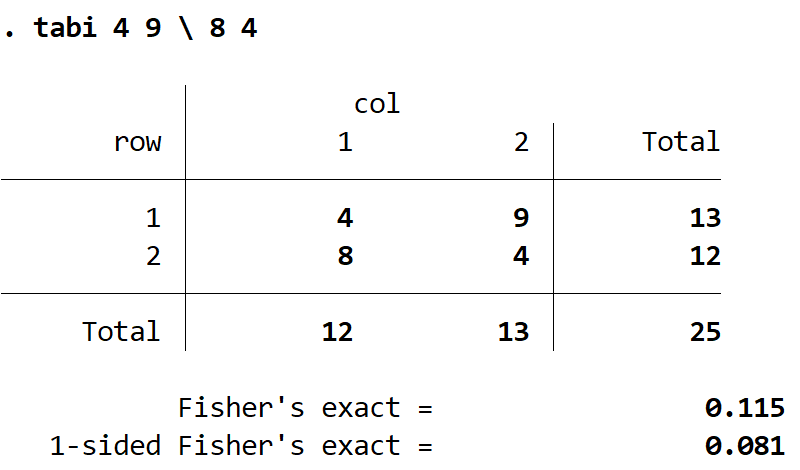
Oto jak zinterpretować wynik:
Tabela wyjściowa: Ta tabela pokazuje liczniki dla każdej komórki, tak jak je wprowadziliśmy.
Dokładny Fisher’s: Jest to wartość p powiązana z dwustronnym dokładnym testem Fishera. W tym przypadku jest to 0,115.
Jednostronny dokładny test Fishera: Jest to wartość p powiązana z jednostronnym dokładnym testem Fishera. W tym przypadku jest to 0,081.
Hipotezą zerową dokładnego testu Fishera jest to, że obie zmienne są niezależne. W tym przypadku naszą hipotezą zerową jest to, że preferencje dotyczące płci i partii politycznych są niezależne, co jest testem dwustronnym, zatem użylibyśmy pierwszej wartości p wynoszącej 0,115.
Ponieważ ta wartość p jest nie mniejsza niż 0,05, nie odrzucamy hipotezy zerowej. Nie mamy zatem wystarczających dowodów, aby stwierdzić, że istnieje znaczący związek między płcią a preferencjami partii politycznych.