Dopasowywanie krzywych w pythonie (z przykładami)

Często możesz chcieć dopasować krzywą do zbioru danych w Pythonie.

Poniższy przykład wyjaśnia krok po kroku, jak dopasować krzywe do danych w Pythonie za pomocą funkcji numpy.polyfit() i jak określić, która krzywa najlepiej pasuje do danych.

Krok 1: Utwórz i wizualizuj dane

Zacznijmy od utworzenia fałszywego zbioru danych, a następnie utwórz wykres rozrzutu w celu wizualizacji danych:

 import pandas as pd
import matplotlib. pyplot as plt

#createDataFrame
df = pd. DataFrame ({' x ': [1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15],
                   ' y ': [3, 14, 23, 25, 23, 15, 9, 5, 9, 13, 17, 24, 32, 36, 46]})

#create scatterplot of x vs. y
plt. scatter (df. x , df. y ) 

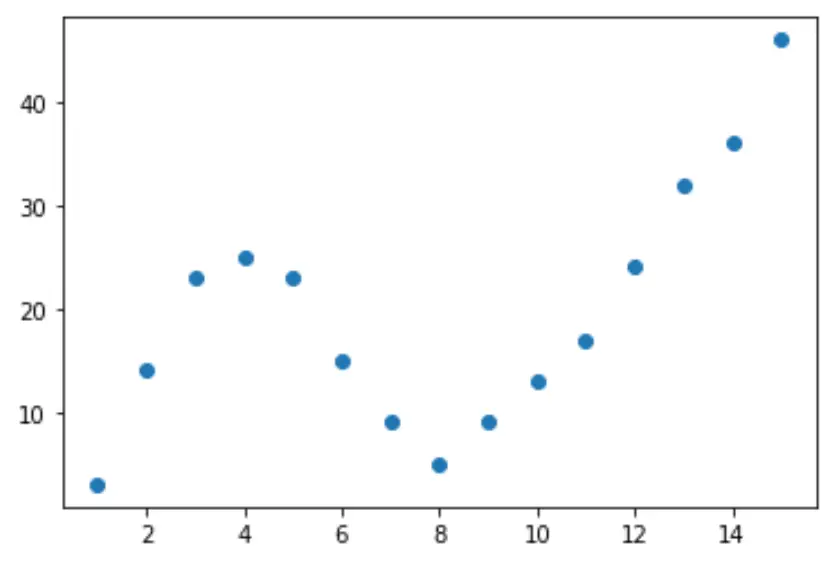
Krok 2: Dostosuj wiele krzywych

Dopasujmy następnie do danych kilka modeli regresji wielomianowej i zwizualizujmy krzywą każdego modelu na tym samym wykresie:

 import numpy as np

#fit polynomial models up to degree 5
model1 = np. poly1d (np. polyfit (df. x , df. y , 1))
model2 = np. poly1d (np. polyfit (df. x , df. y , 2))
model3 = np. poly1d (np. polyfit (df. x , df. y , 3))
model4 = np. poly1d (np. polyfit (df. x , df. y , 4))
model5 = np. poly1d (np. polyfit (df. x , df. y , 5))

#create scatterplot
polyline = np. linspace (1, 15, 50)
plt. scatter (df. x , df. y )

#add fitted polynomial lines to scatterplot 
plt. plot (polyline, model1(polyline), color=' green ')
plt. plot (polyline, model2(polyline), color=' red ')
plt. plot (polyline, model3(polyline), color=' purple ')
plt. plot (polyline, model4(polyline), color=' blue ')
plt. plot (polyline, model5(polyline), color=' orange ')
plt. show ()

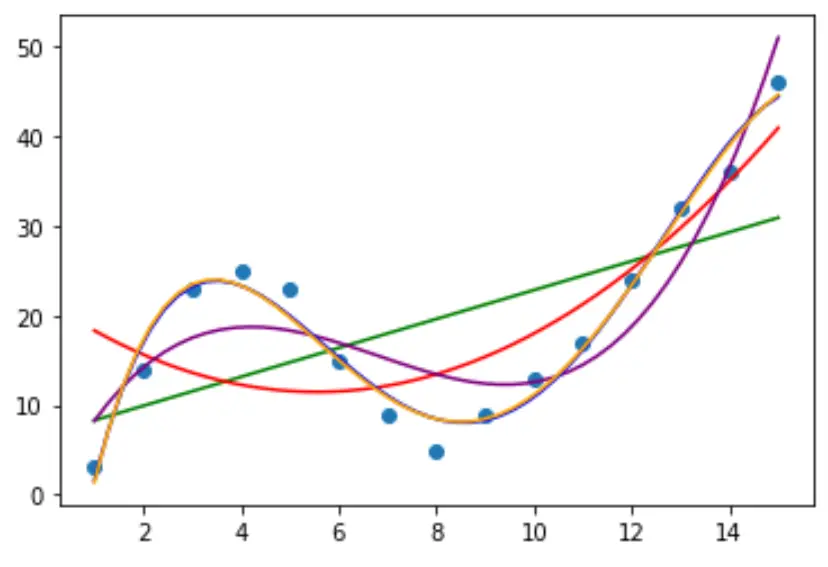
Aby określić, która krzywa najlepiej pasuje do danych, możemy spojrzeć na skorygowany kwadrat R każdego modelu.

Wartość ta mówi nam, jaki procent zmienności zmiennej odpowiedzi można wyjaśnić za pomocą zmiennych predykcyjnych w modelu, skorygowanych o liczbę zmiennych predykcyjnych.

 #define function to calculate adjusted r-squared
def adjR(x, y, degree):
    results = {}
    coeffs = np. polyfit (x, y, degree)
    p = np. poly1d (coeffs)
    yhat = p(x)
    ybar = np. sum (y)/len(y)
    ssreg = np. sum ((yhat-ybar)**2)
    sstot = np. sum ((y - ybar)**2)
    results[' r_squared '] = 1- (((1-(ssreg/sstot))*(len(y)-1))/(len(y)-degree-1))

    return results

#calculated adjusted R-squared of each model
adjR(df. x , df. y , 1)
adjR(df. x , df. y , 2)
adjR(df. x , df. y , 3)
adjR(df. x , df. y , 4)
adjR(df. x , df. y , 5)

{'r_squared': 0.3144819}
{'r_squared': 0.5186706}
{'r_squared': 0.7842864}
{'r_squared': 0.9590276}
{'r_squared': 0.9549709}

Z wyniku widać, że model z najwyższym skorygowanym współczynnikiem R-kwadrat jest wielomianem czwartego stopnia, którego skorygowany współczynnik R-kwadrat wynosi 0,959 .

Krok 3: Wizualizuj ostateczną krzywą

Na koniec możemy utworzyć wykres punktowy z krzywą modelu wielomianowego czwartego stopnia:

 #fit fourth-degree polynomial
model4 = np. poly1d (np. polyfit (df. x , df. y , 4))

#define scatterplot
polyline = np. linspace (1, 15, 50)
plt. scatter (df. x , df. y )

#add fitted polynomial curve to scatterplot
plt. plot (polyline, model4(polyline), ' -- ', color=' red ')
plt. show ()

Równanie dla tej linii możemy również uzyskać za pomocą funkcji print() :

 print (model4)

          4 3 2
-0.01924x + 0.7081x - 8.365x + 35.82x - 26.52

Równanie krzywej jest następujące:

y = -0,01924x ⁴ + 0,7081x ³ – 8,365x ² + 35,82x – 26,52

Możemy użyć tego równania do przewidzenia wartościzmiennej odpowiedzi na podstawie zmiennych predykcyjnych w modelu. Na przykład, jeśli x = 4, to przewidywalibyśmy, że y = 23,32 :

y = -0,0192(4) ⁴ + 0,7081(4) ³ – 8,365(4) ² + 35,82(4) – 26,52 = 23,32

Dodatkowe zasoby

Wprowadzenie do regresji wielomianowej
Jak wykonać regresję wielomianową w Pythonie