Jak dopasować drzewa klasyfikacji i regresji w r

Gdy związek między zestawem zmiennych predykcyjnych a zmienną odpowiedzi jest liniowy, metody takie jak wielokrotna regresja liniowa mogą stworzyć dokładne modele predykcyjne.

Jeśli jednak związek między zestawem predyktorów a reakcją jest bardziej złożony, metody nieliniowe często pozwalają na uzyskanie dokładniejszych modeli.

Jedną z takich metod są drzewa klasyfikacji i regresji (CART), które wykorzystują zestaw zmiennych predykcyjnych do tworzenia drzew decyzyjnych, które przewidują wartość zmiennej odpowiedzi.

Jeśli zmienna odpowiedzi jest ciągła, możemy zbudować drzewa regresji, a jeśli zmienna odpowiedzi jest jakościowa, możemy zbudować drzewa klasyfikacyjne.

W tym samouczku wyjaśniono, jak tworzyć drzewa regresji i klasyfikacji w języku R.

Przykład 1: Budowanie drzewa regresji w R

W tym przykładzie wykorzystamy zbiór danych Hitters z pakietu ISLR , który zawiera różne informacje na temat 263 zawodowych graczy w baseball.

Wykorzystamy ten zbiór danych do skonstruowania drzewa regresji, które wykorzystuje zmienne predykcyjne home runów i lat rozegranych w celu przewidzenia wynagrodzenia danego gracza.

Aby utworzyć to drzewo regresji, wykonaj następujące kroki.

Krok 1: Załaduj niezbędne pakiety.

Najpierw załadujemy niezbędne pakiety dla tego przykładu:

 library (ISLR) #contains Hitters dataset
library (rpart) #for fitting decision trees
library (rpart.plot) #for plotting decision trees

Krok 2: Zbuduj początkowe drzewo regresji.

Najpierw zbudujemy duże drzewo regresji początkowej. Możemy zagwarantować, że drzewo będzie duże, używając małej wartości cp , która oznacza „parametr złożoności”.

Oznacza to, że będziemy dokonywać dalszych podziałów na drzewie regresji, o ile całkowity współczynnik R-kwadrat modelu wzrośnie co najmniej o wartość określoną przez cp.

Następnie użyjemy funkcji printcp() do wydrukowania wyników modelu:

 #build the initial tree
tree <- rpart(Salary ~ Years + HmRun, data=Hitters, control=rpart. control (cp= .0001 ))

#view results
printcp(tree)

Variables actually used in tree construction:
[1] HmRun Years

Root node error: 53319113/263 = 202734

n=263 (59 observations deleted due to missingness)

           CP nsplit rel error xerror xstd
1 0.24674996 0 1.00000 1.00756 0.13890
2 0.10806932 1 0.75325 0.76438 0.12828
3 0.01865610 2 0.64518 0.70295 0.12769
4 0.01761100 3 0.62652 0.70339 0.12337
5 0.01747617 4 0.60891 0.70339 0.12337
6 0.01038188 5 0.59144 0.66629 0.11817
7 0.01038065 6 0.58106 0.65697 0.11687
8 0.00731045 8 0.56029 0.67177 0.11913
9 0.00714883 9 0.55298 0.67881 0.11960
10 0.00708618 10 0.54583 0.68034 0.11988
11 0.00516285 12 0.53166 0.68427 0.11997
12 0.00445345 13 0.52650 0.68994 0.11996
13 0.00406069 14 0.52205 0.68988 0.11940
14 0.00264728 15 0.51799 0.68874 0.11916
15 0.00196586 16 0.51534 0.68638 0.12043
16 0.00016686 17 0.51337 0.67577 0.11635
17 0.00010000 18 0.51321 0.67576 0.11615
n=263 (59 observations deleted due to missingness)

Krok 3: Przytnij drzewo.

Następnie przycinamy drzewo regresji, aby znaleźć optymalną wartość cp (parametr złożoności), która prowadzi do najniższego błędu testu.

Należy zauważyć, że optymalną wartością cp jest ta, która prowadzi do najniższego błędu x w poprzednim wyniku, co reprezentuje błąd obserwacji z danych pochodzących z walidacji krzyżowej.

 #identify best cp value to use
best <- tree$cptable[which. min (tree$cptable[," xerror "])," CP "]

#produce a pruned tree based on the best cp value
pruned_tree <- prune (tree, cp=best)

#plot the pruned tree
prp(pruned_tree,
    faclen= 0 , #use full names for factor labels
    extra= 1 , #display number of obs. for each terminal node
    roundint= F , #don't round to integers in output
    digits= 5 ) #display 5 decimal places in output

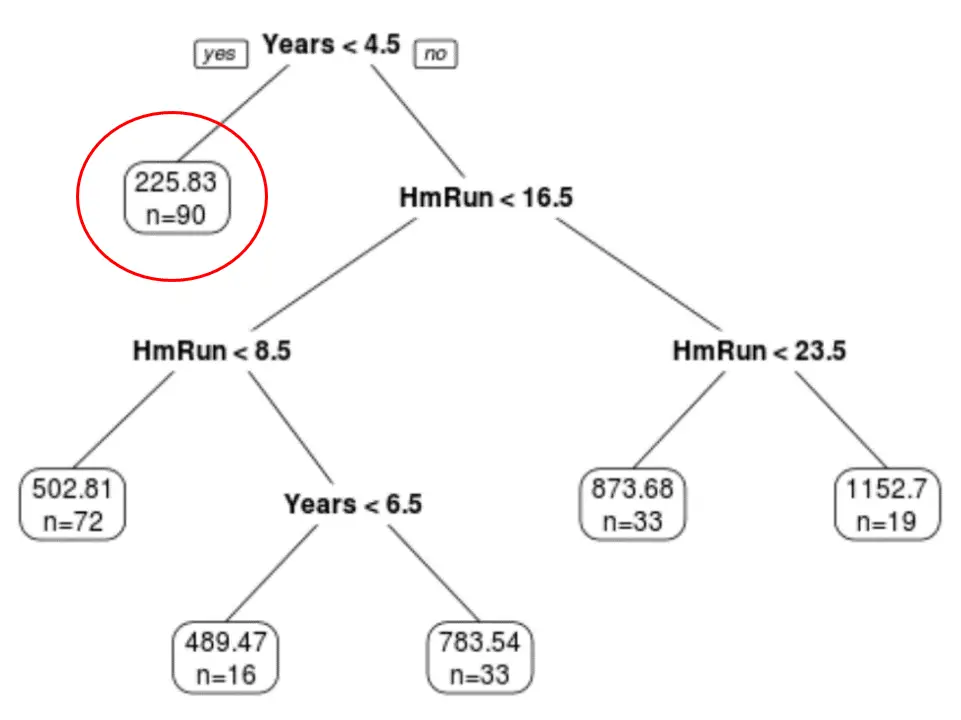
Widzimy, że ostatecznie przycięte drzewo ma sześć węzłów końcowych. Każdy węzeł liścia wyświetla przewidywaną pensję graczy w tym węźle, a także liczbę obserwacji z oryginalnego zbioru danych, które należą do tej klasy.

Na przykład widzimy, że w oryginalnym zbiorze danych było 90 graczy z doświadczeniem krótszym niż 4,5 roku, a ich średnia pensja wyniosła 225,83 tys. dolarów.

Krok 4: Użyj drzewa do przewidywania.

Możemy wykorzystać ostatecznie przycięte drzewo, aby przewidzieć pensję danego gracza na podstawie jego wieloletniego doświadczenia i średnich home runów.

Na przykład gracz, który ma 7 lat doświadczenia i średnio 4 home runy, ma oczekiwaną pensję w wysokości 502,81 tys. dolarów .

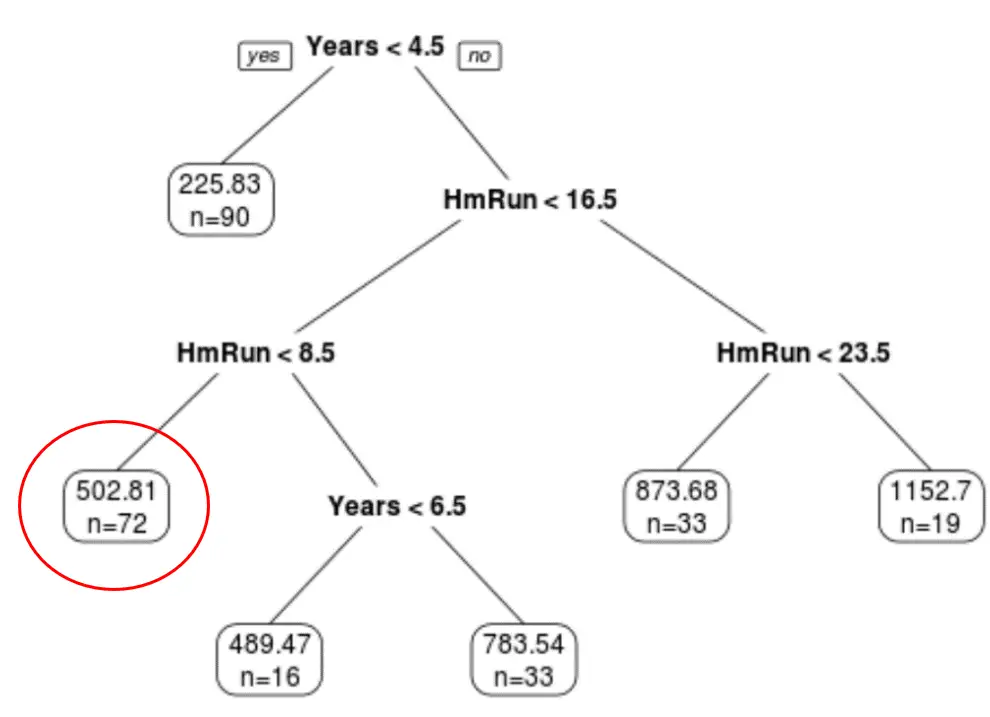
Aby to potwierdzić, możemy użyć funkcji przewidywania() w R:

 #define new player
new <- data.frame(Years=7, HmRun=4)

#use pruned tree to predict salary of this player
predict(pruned_tree, newdata=new)

502.8079

Przykład 2: Budowa drzewa klasyfikacyjnego w R

W tym przykładzie wykorzystamy zbiór danych ptitanic z pakietu rpart.plot , który zawiera różne informacje o pasażerach na pokładzie Titanica.

Wykorzystamy ten zbiór danych do stworzenia drzewa klasyfikacyjnego, które wykorzystuje zmienne predykcyjne class , płeć i wiek do przewidzenia, czy dany pasażer przeżył, czy nie.

Aby utworzyć to drzewo klasyfikacji, wykonaj następujące kroki.

Krok 1: Załaduj niezbędne pakiety.

Najpierw załadujemy niezbędne pakiety dla tego przykładu:

 library (rpart) #for fitting decision trees
library (rpart.plot) #for plotting decision trees

Krok 2: Zbuduj początkowe drzewo klasyfikacji.

Najpierw zbudujemy duże drzewo klasyfikacji początkowej. Możemy zagwarantować, że drzewo będzie duże, używając małej wartości cp , która oznacza „parametr złożoności”.

Oznacza to, że będziemy dokonywać dalszych podziałów na drzewie klasyfikacyjnym, o ile ogólne dopasowanie modelu wzrośnie co najmniej o wartość określoną przez cp.

Następnie użyjemy funkcji printcp() do wydrukowania wyników modelu:

 #build the initial tree
tree <- rpart(survived~pclass+sex+age, data=ptitanic, control=rpart. control (cp= .0001 ))

#view results
printcp(tree)

Variables actually used in tree construction:
[1] age pclass sex   

Root node error: 500/1309 = 0.38197

n=1309 

      CP nsplit rel error xerror xstd
1 0.4240 0 1.000 1.000 0.035158
2 0.0140 1 0.576 0.576 0.029976
3 0.0095 3 0.548 0.578 0.030013
4 0.0070 7 0.510 0.552 0.029517
5 0.0050 9 0.496 0.528 0.029035
6 0.0025 11 0.486 0.532 0.029117
7 0.0020 19 0.464 0.536 0.029198
8 0.0001 22 0.458 0.528 0.029035

Krok 3: Przytnij drzewo.

Następnie przycinamy drzewo regresji, aby znaleźć optymalną wartość cp (parametr złożoności), która prowadzi do najniższego błędu testu.

Należy zauważyć, że optymalną wartością cp jest ta, która prowadzi do najniższego błędu x w poprzednim wyniku, co reprezentuje błąd obserwacji z danych pochodzących z walidacji krzyżowej.

 #identify best cp value to use
best <- tree$cptable[which. min (tree$cptable[," xerror "])," CP "]

#produce a pruned tree based on the best cp value
pruned_tree <- prune (tree, cp=best)

#plot the pruned tree
prp(pruned_tree,
    faclen= 0 , #use full names for factor labels
    extra= 1 , #display number of obs. for each terminal node
    roundint= F , #don't round to integers in output
    digits= 5 ) #display 5 decimal places in output

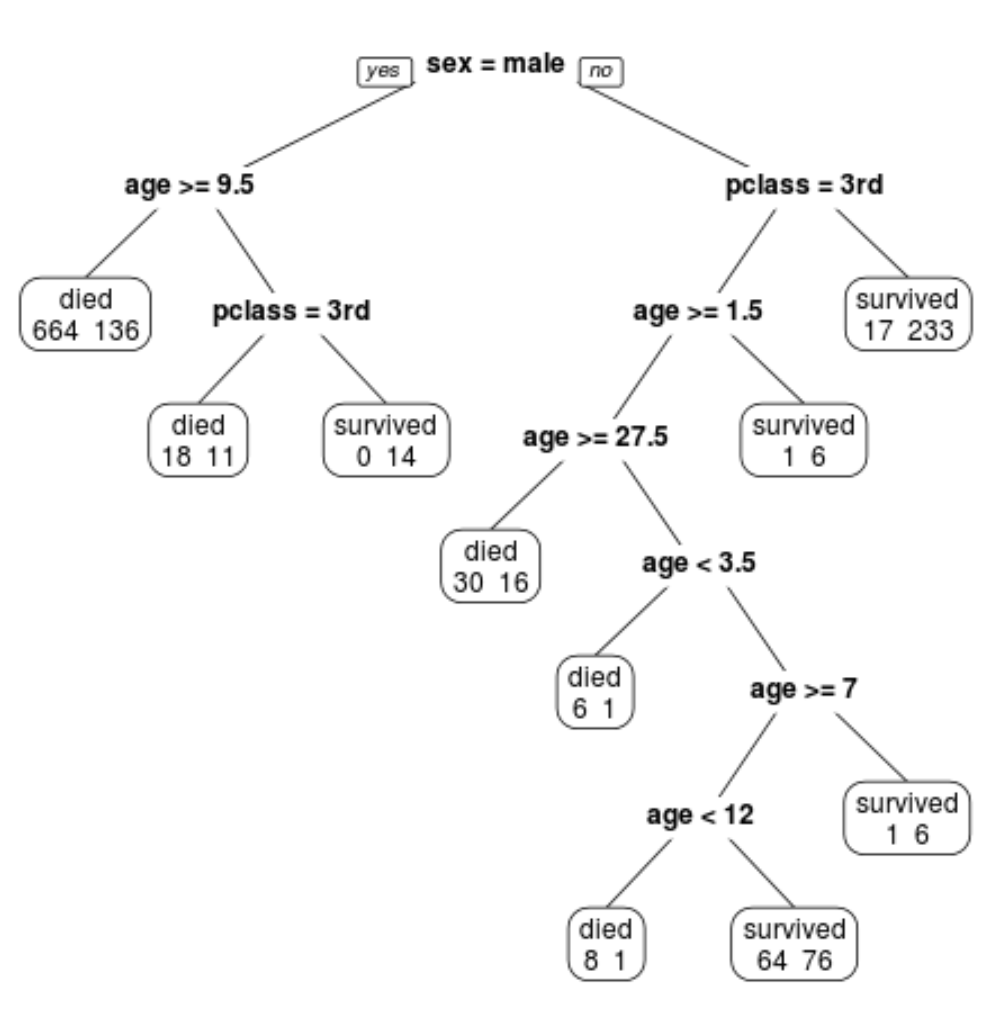
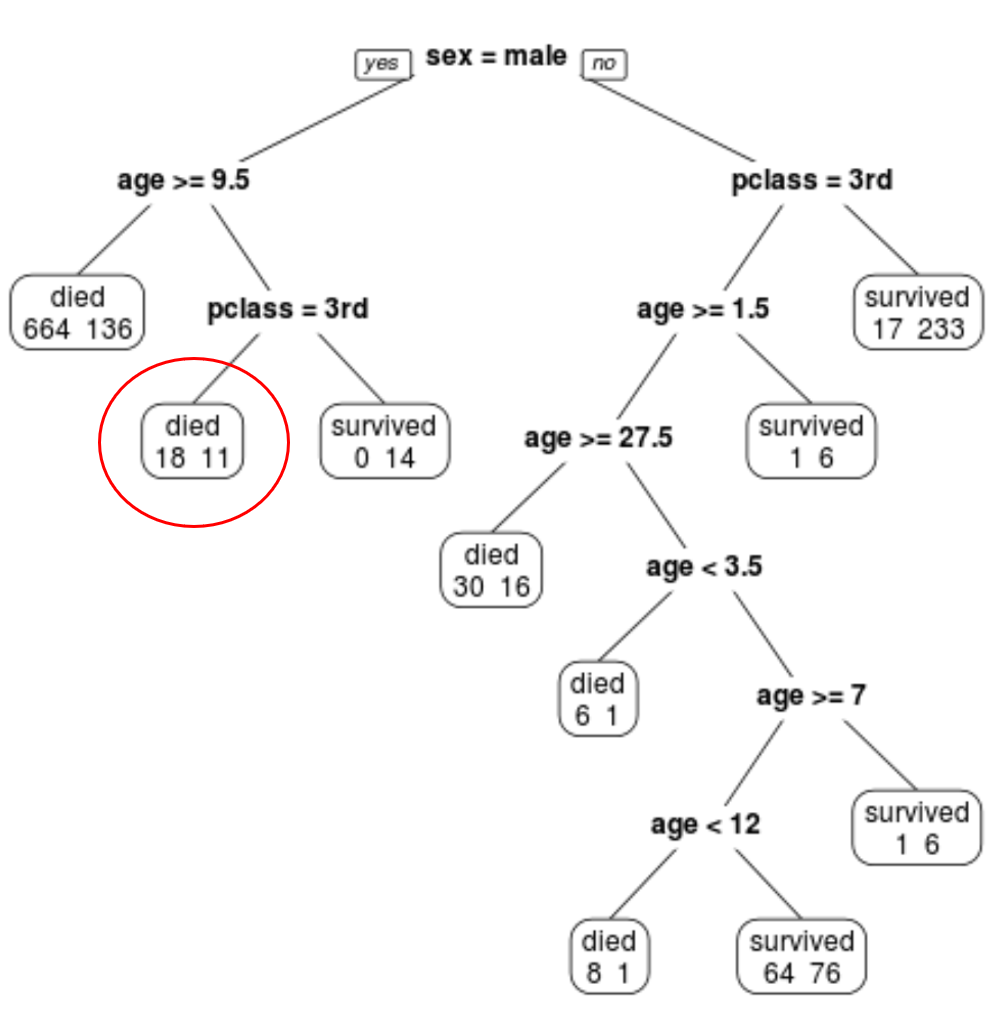
Widzimy, że ostatecznie przycięte drzewo ma 10 węzłów końcowych. Każdy węzeł końcowy wskazuje liczbę pasażerów, którzy zginęli, a także liczbę ocalałych.

Na przykład w lewym węźle widzimy, że zginęło 664 pasażerów, a 136 przeżyło.

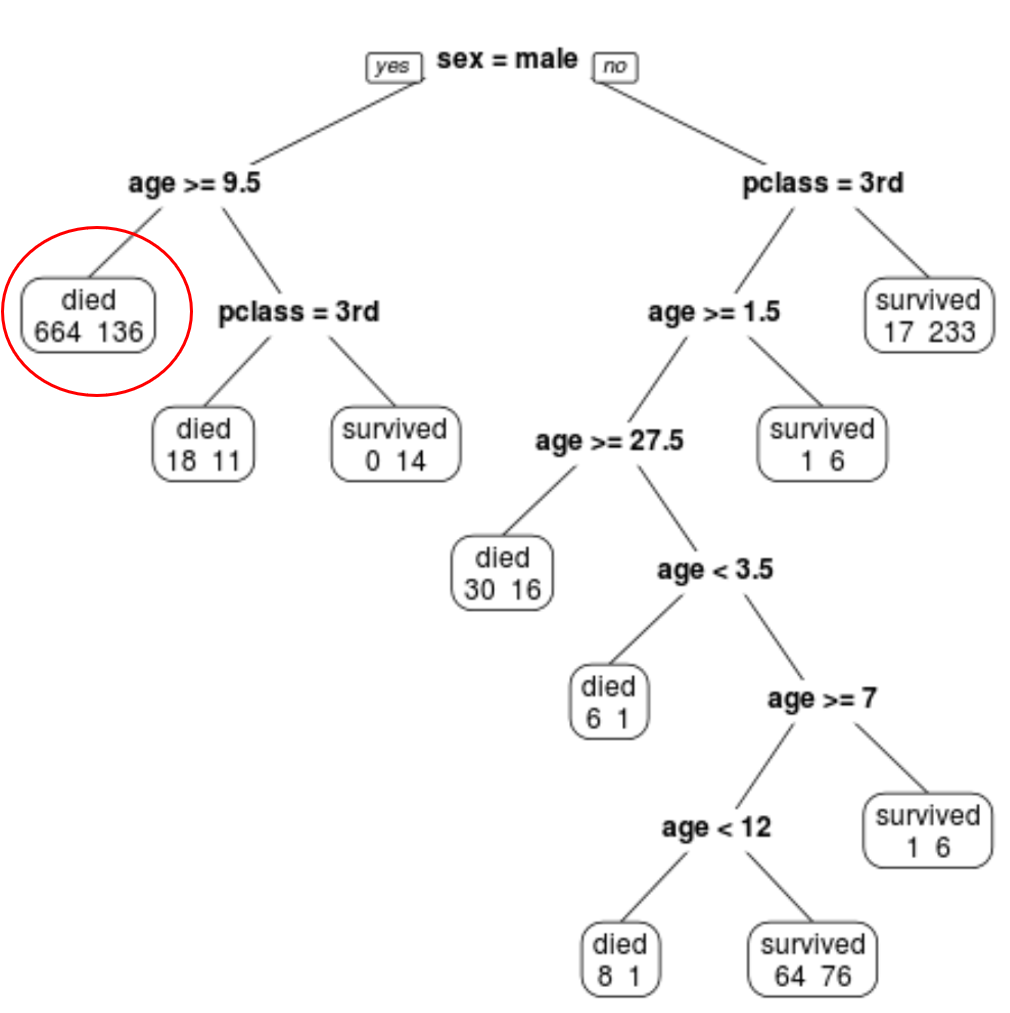
Krok 4: Użyj drzewa do przewidywania.

Możemy wykorzystać ostatnie przycięte drzewo, aby przewidzieć prawdopodobieństwo przeżycia danego pasażera na podstawie jego klasy, wieku i płci.

Przykładowo, prawdopodobieństwo przeżycia pasażera płci męskiej w wieku 8 lat i podróżującego w pierwszej klasie wynosi 11/29 = 37,9%.

Pełny kod R użyty w tych przykładach można znaleźć tutaj .