Jak wykonać test t dla dwóch próbek w programie excel
Test t dla dwóch prób służy do sprawdzenia, czy średnie z dwóch populacji są równe, czy nie.
W tym samouczku wyjaśniono, jak wykonać test t dla dwóch próbek w programie Excel.
Jak wykonać test t dla dwóch próbek w programie Excel
Załóżmy, że badacze chcą wiedzieć, czy dwa różne gatunki roślin w danym kraju mają tę samą średnią wysokość. Ponieważ obejście i zmierzenie każdej rośliny zajęłoby zbyt dużo czasu, postanowiono pobrać próbkę 20 roślin każdego gatunku.
Poniższy obrazek przedstawia wysokość (w calach) każdej rośliny w każdej próbce:
Możemy wykonać test t dla dwóch próbek, aby określić, czy oba gatunki mają ten sam średni wzrost, wykonując następujące kroki:
Krok 1: Ustal, czy wariancje populacji są równe .
Kiedy przeprowadzamy test t dla dwóch prób, musimy najpierw zdecydować, czy założymy, że obie populacje mają równe czy nierówne wariancje. Ogólnie rzecz biorąc, możemy założyć, że populacje mają równe wariancje, jeśli stosunek wariancji największej próbki do wariancji najmniejszej próbki jest mniejszy niż 4:1.
Wariancję dla każdej próbki możemy znaleźć za pomocą funkcji Excela =VAR.S(Zakres komórek) , jak pokazano na poniższym obrazku:
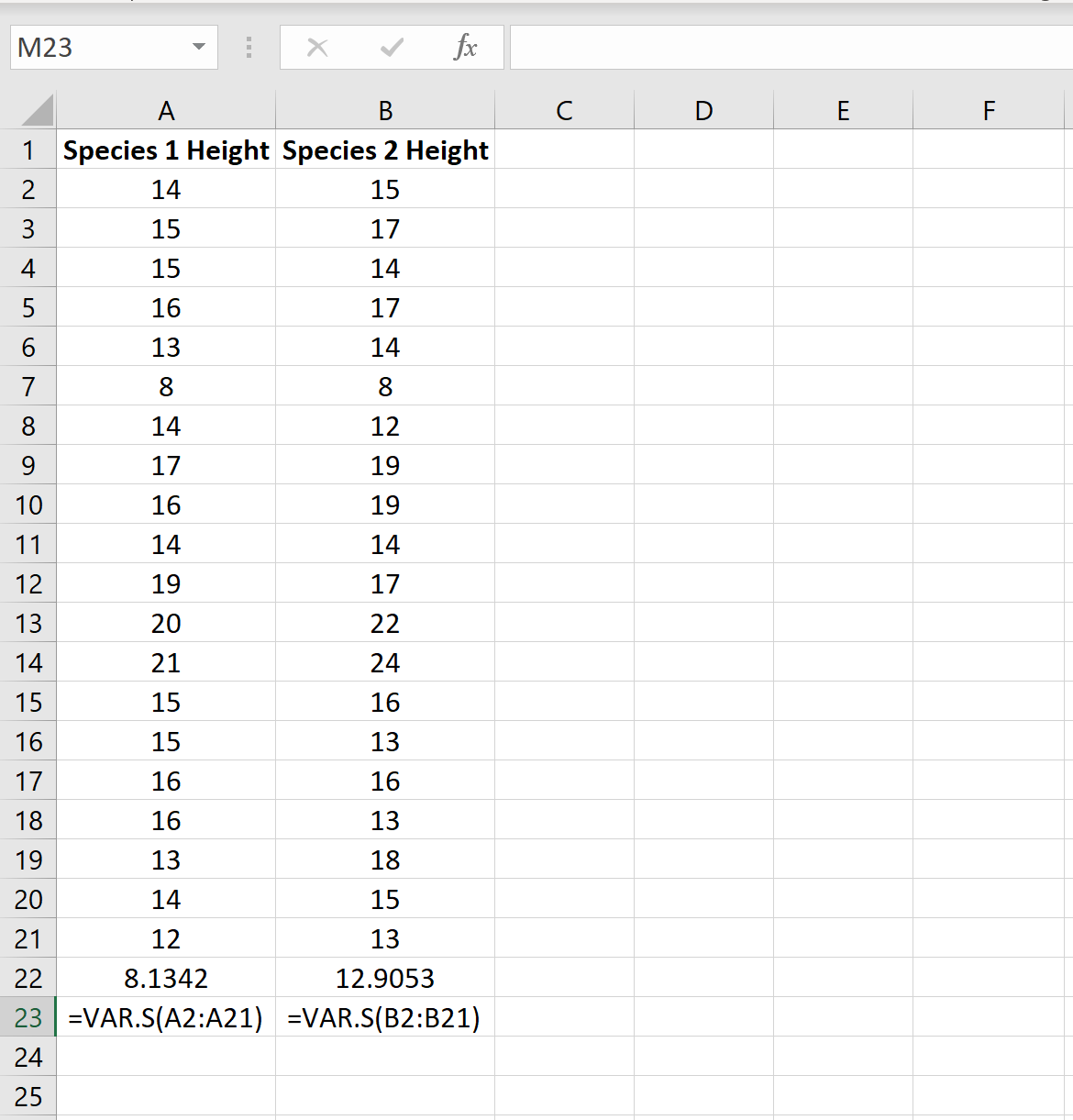
Stosunek wariancji największej próby do wariancji najmniejszej próbki wynosi 12,9053/8,1342 = 1,586 , czyli mniej niż 4. Oznacza to, że możemy założyć, że wariancje populacji są równe.
Krok 2: Otwórz pakiet narzędzi analitycznych .
Na karcie Dane na górnej wstążce kliknij „Analiza danych”.
Jeśli nie widzisz tej opcji kliknięcia, musisz najpierw pobrać pakiet narzędzi analitycznych , który jest całkowicie bezpłatny.
Krok 3: Wybierz odpowiedni test do użycia.
Wybierz opcję, która mówi, że test t: dwie próbki przy założeniu równych wariancji , a następnie kliknij OK.
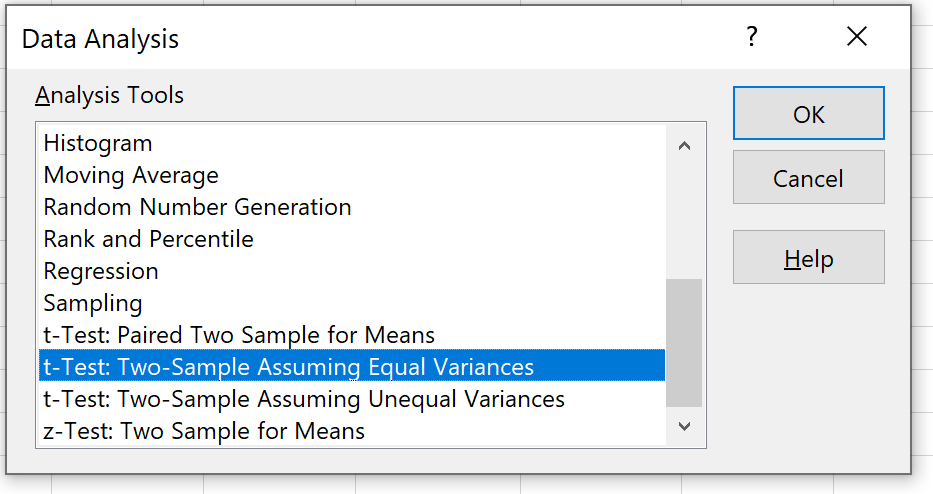
Krok 4: Wprowadź niezbędne informacje .
Wprowadź zakres wartości zmiennej 1 (nasza pierwsza próba), zmiennej 2 (nasza druga próba), hipotetyczną różnicę średnią (w tym przypadku wpisujemy „0”, ponieważ chcemy wiedzieć, czy prawdziwa różnica średnich populacji wynosi 0) oraz zakres wyjściowy, w jakim chcielibyśmy zobaczyć wyświetlane wyniki testu t. Następnie kliknij OK.
Krok 5: Interpretacja wyników .
Po kliknięciu przycisku OK w poprzednim kroku zostaną wyświetlone wyniki testu t.
Oto jak interpretować wyniki:
Średnia: Jest to średnia z każdej próbki. Próbka 1 ma średnią wysokość 15,15 , a próbka 2 ma średnią wysokość 15,8 .
Wariancja: Jest to wariancja dla każdej próbki. Próbka 1 ma wariancję 8,13 , a próbka 2 ma wariancję 12,90 .
Obserwacje: Jest to liczba obserwacji w każdej próbce. Obie próbki zawierają 20 obserwacji (np. 20 pojedynczych roślin w każdej próbce).
Wariancja łączna: liczba obliczona poprzez „łączenie” wariancji każdej próbki przy użyciu wzoru s 2 p = [ (n 1 -1) s 2 1 + (n 2 -1) s 2 2 ] / (n 1 + n 2 – 2), co okazuje się wynosić 10,51974 . Liczba ta jest następnie wykorzystywana przy obliczaniu statystyki testu t .
Hipotetyczna średnia różnica: liczba, na temat której „stawiamy hipotezę”, to różnica między średnimi z dwóch populacji. W tym przypadku wybraliśmy 0 , ponieważ chcemy sprawdzić, czy różnica między średnimi z dwóch populacji jest równa 0, na przykład jeśli nie ma różnicy.
df: Stopnie swobody testu t, obliczone jako n 1 + n 2 -2 = 20 + 20 – 2 = 38 .
t Stat: Statystyka testowa t , obliczona jako t = [ x 1 – x 2 ] / √ [s 2 p (1/n 1 + 1/n 2 )]
W tym przypadku t = [15,15-15,8] / √ [10,51974(1/20+1/20)] = -0,63374 .
Dwustronny P(T<=t): wartość p dla dwustronnego testu t. W tym przypadku p = 0,530047 . Jest to znacznie więcej niż alfa = 0,05, więc nie możemy odrzucić hipotezy zerowej. Nie mamy wystarczających dowodów, aby stwierdzić, że średnie w obu populacjach są różne.
t Dwustronny krytyczny: Jest to wartość krytyczna testu, określona poprzez identyfikację wartości w tabeli rozkładu t, która odpowiada dwustronnemu testowi z alfa = 0,05 i df = 38. Okazuje się, że wynosi 2, 024394 . Ponieważ nasza statystyka testu t jest mniejsza niż ta wartość, nie możemy odrzucić hipotezy zerowej. Nie mamy wystarczających dowodów, aby stwierdzić, że średnie w obu populacjach są różne.
Należy zauważyć, że podejście oparte na wartości p i wartości krytycznej doprowadzi do tego samego wniosku.
Dodatkowe zasoby
Poniższe samouczki wyjaśniają, jak wykonywać inne typy testów t w programie Excel:
Jak wykonać test t dla jednej próby w programie Excel
Jak wykonać test t dla par próbek w programie Excel
o autorze
Dr Benjamin Anderson
Cześć, jestem Benjamin i jestem emerytowanym profesorem statystyki, który został oddanym nauczycielem Statorials. Dzięki bogatemu doświadczeniu i wiedzy specjalistycznej w dziedzinie statystyki chętnie dzielę się swoją wiedzą, aby wzmocnić pozycję uczniów za pośrednictwem Statorials. Wiedzieć więcej