Jak wykonać test t dla dwóch próbek na kalkulatorze ti-84

Test t dla dwóch prób służy do sprawdzenia, czy średnie z dwóch populacji są równe, czy nie.

W tym samouczku wyjaśniono, jak wykonać test t dla dwóch próbek na kalkulatorze TI-84.

Przykład: Test t dla dwóch próbek na kalkulatorze TI-84

Naukowcy chcą wiedzieć, czy nowy sposób uzdatniania paliwa powoduje zmianę średniego zużycia paliwa przez określony samochód. Aby to sprawdzić, przeprowadzają eksperyment, w którym 12 samochodów otrzymuje nowe uzdatnienie paliwa, a 12 samochodów nie. W grupie kontrolnej średnia wartość mpg wynosi 21 mpg, a odchylenie standardowe wynosi 2,73 mpg. W grupie leczonej średnia wartość mpg wynosi 22,75 mpg, a odchylenie standardowe wynosi 3,25 mpg.

Skorzystaj z tych danych, aby wykonać test t dla dwóch próbek, aby określić, czy średnia mpg różni się w obu grupach.

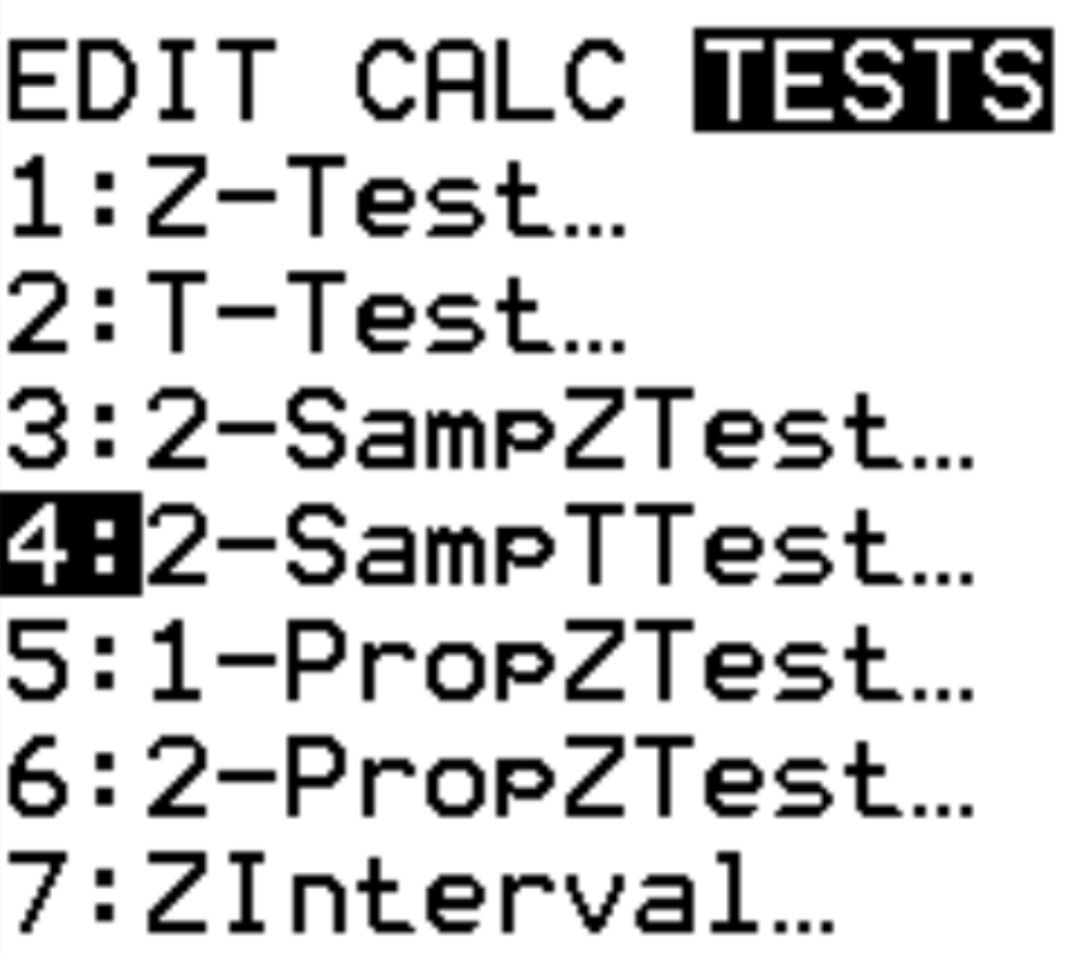
Krok 1: Wybierz opcję 2-SampTTest.

Kliknij Statystyka . Przewiń w dół do TESTY. Przewiń do 2-SampTTest i naciśnij ENTER .

Krok 2: Podaj niezbędne informacje.

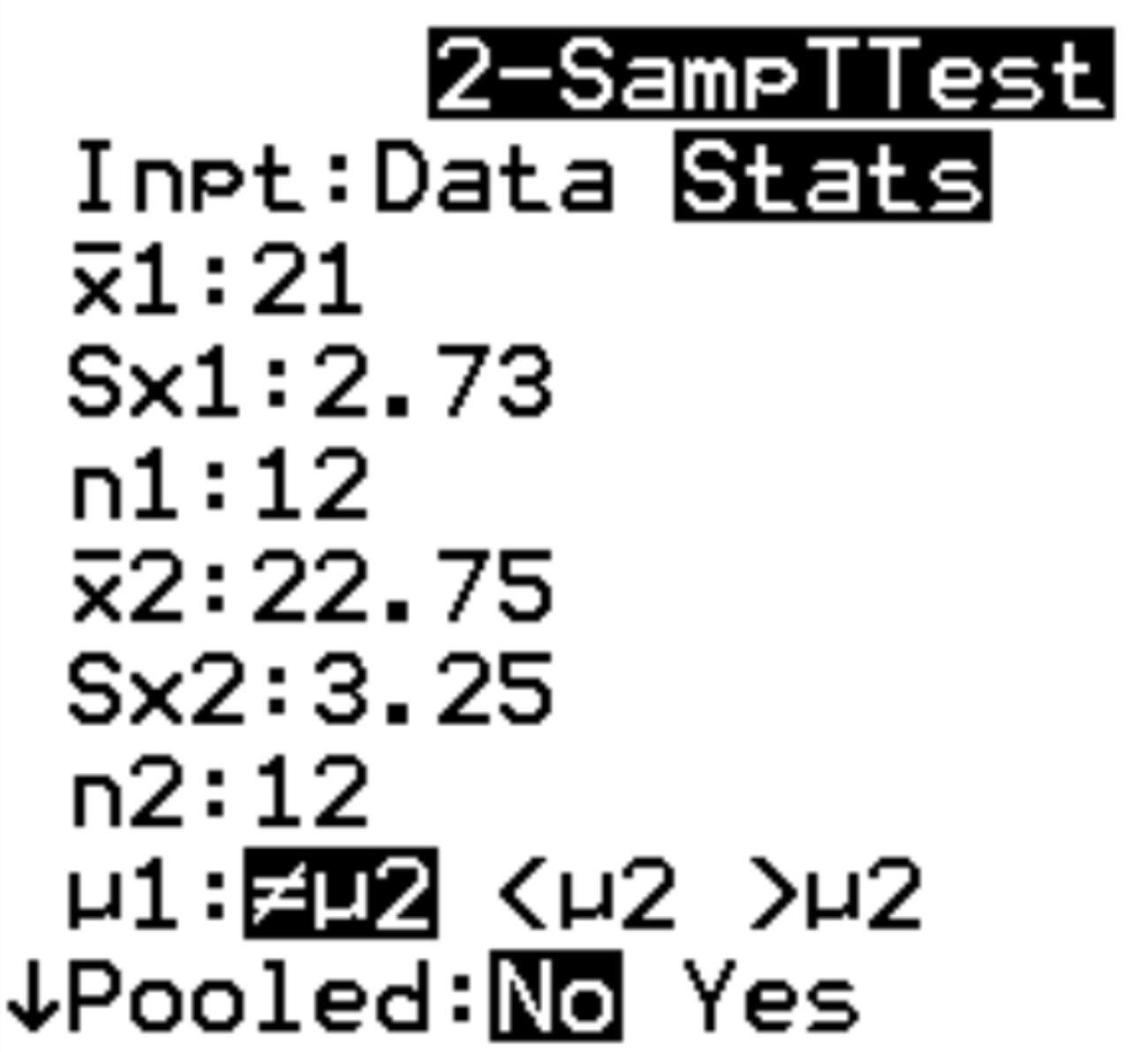
Kalkulator poprosi o podanie następujących informacji:

• Dane wejściowe: Wybierz, czy pracujesz z surowymi danymi (Dane), czy ze statystykami podsumowującymi (Statystyki). W takim przypadku podświetlimy Statystyki i wciśniemy ENTER .
• x 1: średnie próbki z pierwszej grupy. Wpiszemy 21 i wciśnijmy ENTER .
• Sx1: odchylenie standardowe próbki pierwszej grupy. Wpiszemy 2.73 i wciśnijmy ENTER .
• n1: Wielkość próby w pierwszej grupie. Wpiszemy 12 i wciśnijmy ENTER .
• x 2: średnia z próby drugiej grupy. Wpiszemy 22,75 i wciśnij ENTER .
• Sx2: odchylenie standardowe próbki drugiej grupy. Wpiszemy 3.25 i wciśnij ENTER .
• n2: wielkość próby drugiej grupy. Wpiszemy 12 i wciśnijmy ENTER .
• μ1 : Alternatywna hipoteza do zastosowania. Ponieważ przeprowadzamy test dwustronny, podświetlimy ≠ μ2 i wciśniemy ENTER . Oznacza to, że naszą alternatywną hipotezą jest μ1≠μ2. Pozostałe dwie opcje zostaną użyte do testowania lewego (μ1<μ2) i prawego (μ1>μ2).
• Połączone: Zdecyduj, czy chcesz połączyć luki obu grup. W większości przypadków wybierzemy nie. Podświetl nie i naciśnij ENTER .

Na koniec podświetl Oblicz i naciśnij ENTER .

Krok 3: Interpretacja wyników.

Nasz kalkulator automatycznie wygeneruje wyniki dwóch przykładów testu t:

Oto jak interpretować wyniki:

• μ ₁ ≠ μ ₂ : Jest to alternatywna hipoteza testu.
• t=-1,42825817 : To jest statystyka testu t.
• p=0,1676749174 : Jest to wartość p odpowiadająca statystyce testowej.
• df=21,36350678: są to stopnie swobody użyte do obliczenia statystyki testowej.
• x1 = ₂₁ . To jest średnia z próby, którą wprowadziliśmy dla pierwszej grupy.
• x ₂ = 22,75: To jest średnia z próby, którą wprowadziliśmy dla drugiej grupy.
• Sx1=2,73 . To jest odchylenie standardowe próbki, które wprowadziliśmy dla pierwszej grupy.
• Sx2=3,25 : To jest odchylenie standardowe próbki, które wprowadziliśmy dla drugiej grupy.
• n1=12: To jest wielkość próby, którą wprowadziliśmy dla pierwszej grupy.
• n2=12: To jest wielkość próby, którą wprowadziliśmy dla drugiej grupy.

Ponieważ wartość p testu (0,1676749174) jest nie mniejsza niż 0,05, nie udaje nam się odrzucić hipotezy zerowej. Oznacza to, że nie mamy wystarczających dowodów, aby stwierdzić, że średnia wartość mpg różni się w obu grupach.