Ujemny dwumian vs poissona: jak wybrać model regresji

Ujemna regresja dwumianowa i regresja Poissona to dwa typy modeli regresji, które należy stosować, gdyzmienna odpowiedzi jest reprezentowana przez wyniki zliczania dyskretnego.

Oto kilka przykładów zmiennych odpowiedzi, które reprezentują dyskretne wyniki zliczania:

• Liczba studentów kończących określony program
• Liczba wypadków drogowych na danym skrzyżowaniu
• Liczba uczestników, którzy ukończyli maraton
• Liczba zwrotów w danym miesiącu w sklepie detalicznym

Jeżeli wariancja jest w przybliżeniu równa średniej, wówczas model regresji Poissona na ogół dobrze pasuje do zbioru danych.

Jeśli jednak wariancja jest znacznie większa niż średnia, model regresji dwumianowej jest na ogół w stanie lepiej dopasować dane.

Istnieją dwie techniki, których możemy użyć, aby określić, czy regresja Poissona czy ujemna regresja dwumianowa jest bardziej odpowiednia dla danego zbioru danych:

1. Działki resztkowe

Możemy stworzyć wykres reszt standaryzowanych względem wartości przewidywanych z modelu regresji.

Jeżeli większość reszt standaryzowanych mieści się w przedziale od -2 do 2, prawdopodobnie odpowiedni będzie model regresji Poissona.

Jeśli jednak wiele reszt wykracza poza ten zakres, prawdopodobnie lepsze dopasowanie zapewni model regresji ujemnej dwumianowej.

2. Test ilorazu wiarygodności

Możemy dopasować model regresji Poissona i model regresji dwumianowej ujemnej do tego samego zestawu danych, a następnie przeprowadzić test współczynnika wiarygodności.

Jeżeli wartość p testu jest poniżej pewnego poziomu istotności (np. 0,05), wówczas możemy stwierdzić, że model regresji dwumianowej ujemnej zapewnia znacznie lepsze dopasowanie.

Poniższy przykład pokazuje, jak użyć tych dwóch technik w języku R, aby określić, czy dla danego zbioru danych lepiej jest zastosować model regresji Poissona czy ujemnego modelu regresji dwumianowej.

Przykład: ujemna regresja dwumianowa vs regresja Poissona

Załóżmy, że chcemy dowiedzieć się, ile stypendiów otrzymuje licealista w baseballu w danym powiecie, biorąc pod uwagę jego oddział szkolny („A”, „B” lub „C”) i ocenę szkolną. egzamin wstępny na uniwersytet (mierzony od 0 do 100). ).

Wykonaj poniższe kroki, aby określić, czy model regresji dwumianowej ujemnej czy model regresji Poissona zapewnia lepsze dopasowanie do danych.

Krok 1: Utwórz dane

Poniższy kod tworzy zbiór danych, z którym będziemy pracować, zawierający dane dotyczące 1000 graczy w baseball:

 #make this example reproducible
set. seeds (1)

#create dataset
data <- data. frame (offers = c(rep(0, 700), rep(1, 100), rep(2, 100),
                              rep(3, 70), rep(4, 30)),
                   division = sample(c(' A ', ' B ', ' C '), 100, replace = TRUE ),
                   exam = c(runif(700, 60, 90), runif(100, 65, 95),
                            runif(200, 75, 95)))

#view first six rows of dataset
head(data)

  offers division exam
1 0 A 66.22635
2 0 C 66.85974
3 0 A 77.87136
4 0 B 77.24617
5 0 A 62.31193
6 0 C 61.06622

Krok 2: Dopasuj model regresji Poissona i model regresji dwumianowej ujemnej

Poniższy kod pokazuje, jak dopasować do danych zarówno model regresji Poissona, jak i model regresji ujemnego dwumianu:

 #fit Poisson regression model
p_model <- glm(offers ~ division + exam, family = ' fish ', data = data)

#fit negative binomial regression model
library (MASS)

nb_model <- glm. nb (offers ~ division + exam, data = data)

Krok 3: Utwórz działki resztkowe

Poniższy kod pokazuje, jak utworzyć wykresy reszt dla obu modeli.

 #Residual plot for Poisson regression
p_res <- resid (p_model)
plot(fitted(p_model), p_res, col=' steelblue ', pch=16,
     xlab=' Predicted Offers ', ylab=' Standardized Residuals ', main=' Poisson ')
abline(0,0)

#Residual plot for negative binomial regression
nb_res <- resid (nb_model)
plot(fitted(nb_model), nb_res, col=' steelblue ', pch=16,
     xlab=' Predicted Offers ', ylab=' Standardized Residuals ', main=' Negative Binomial ')
abline(0,0) 

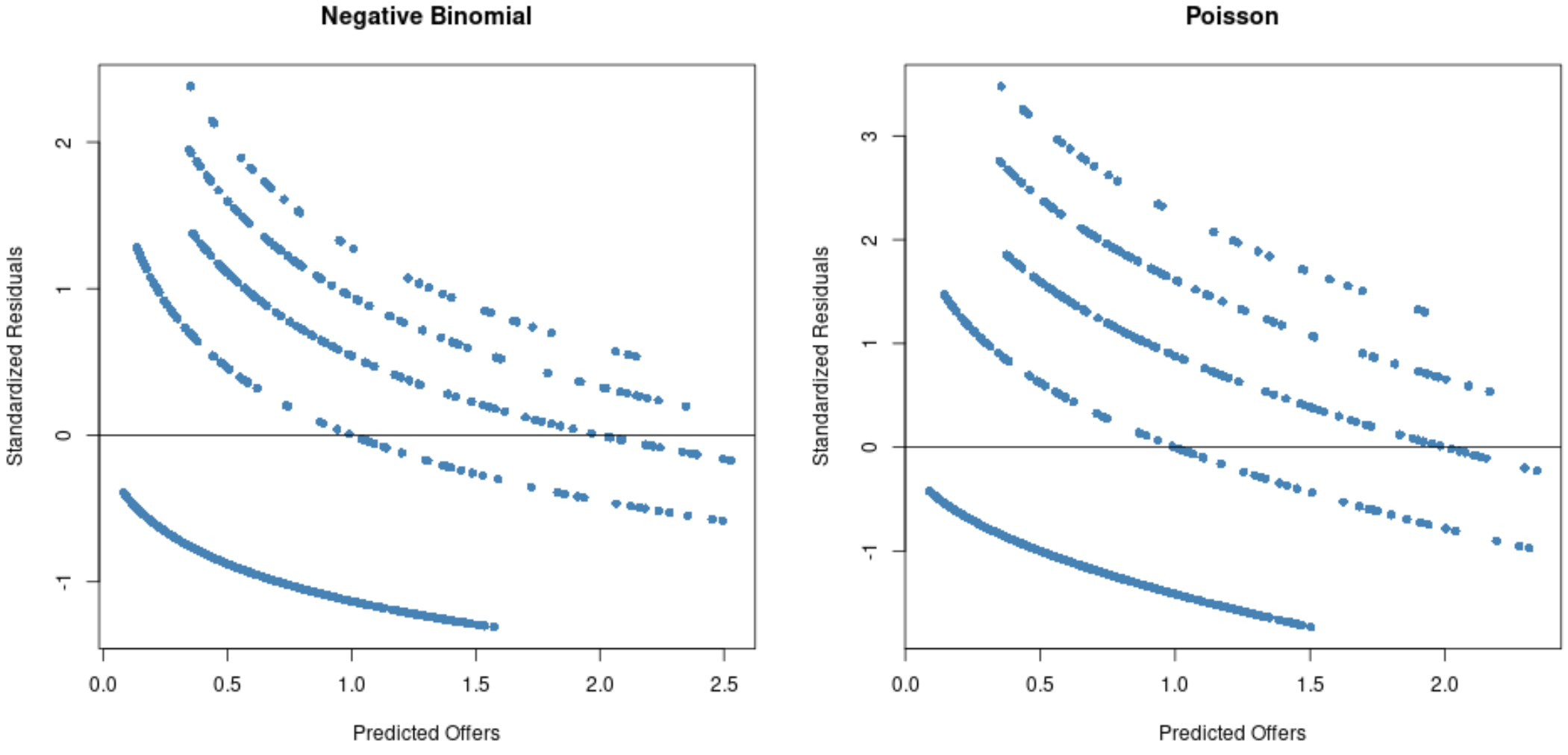
Z wykresów widać, że reszty są bardziej rozłożone w przypadku modelu regresji Poissona (należy zauważyć, że niektóre reszty wykraczają poza 3) w porównaniu z ujemnym modelem regresji dwumianowej.

Oznacza to, że prawdopodobnie bardziej odpowiedni będzie ujemny model regresji dwumianowej, ponieważ reszty tego modelu są mniejsze.

Krok 4: Wykonaj test współczynnika wiarygodności

Na koniec możemy przeprowadzić test współczynnika wiarygodności, aby określić, czy istnieje statystycznie istotna różnica w dopasowaniu dwóch modeli regresji:

 pchisq(2 * ( logLik (nb_model) - logLik (p_model)), df = 1, lower. tail = FALSE )

'log Lik.' 3.508072e-29 (df=5)

Wartość p testu wynosi 3,508072e-29 , czyli jest znacznie mniejsza niż 0,05.

Można zatem stwierdzić, że model regresji dwumianowej ujemnej zapewnia znacznie lepsze dopasowanie do danych w porównaniu z modelem regresji Poissona.

Dodatkowe zasoby

Wprowadzenie do ujemnego rozkładu dwumianowego
Wprowadzenie do rozkładu Poissona