Jak wykonać dwukierunkową anova w sas

Dwuczynnikową analizę ANOVA stosuje się w celu ustalenia, czy istnieje statystycznie istotna różnica między średnimi z trzech lub większej liczby niezależnych grup przypisanych do dwóch zmiennych (czasami nazywanych „czynnikami”).

W tym samouczku przedstawiono krok po kroku przykład wykonania dwukierunkowej analizy ANOVA w SAS-ie.

Krok 1: Utwórz dane

Załóżmy, że botanik chce wiedzieć, czy na wzrost roślin wpływa ekspozycja na światło słoneczne i częstotliwość podlewania.

Sadzi 30 nasion i pozwala im rosnąć przez miesiąc w różnych warunkach nasłonecznienia i częstotliwości podlewania. Po miesiącu rejestruje wysokość każdej rośliny. Wyniki przedstawiono poniżej:

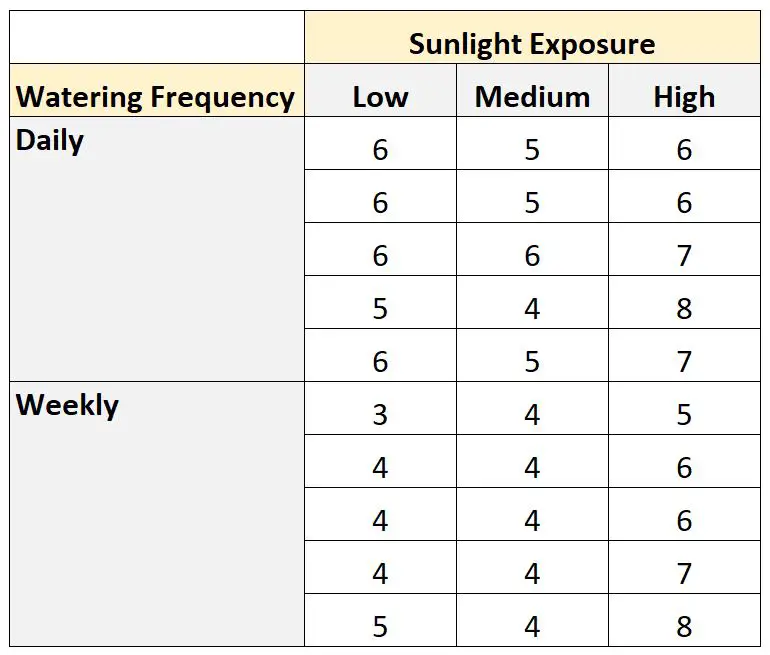
Do utworzenia tego zbioru danych w SAS-ie możemy użyć następującego kodu:

 /*create dataset*/
data my_data;
    input water $sunlight $height;
    datalines ;
daily low 6
daily low 6
daily low 6
daily low 5
daily low 6
daily med 5
daily med 5
daily med 6
daily med 4
daily med 5
daily high 6
daily high 6
daily high 7
daily high 8
daily high 7
weekly low 3
weekly low 4
weekly low 4
weekly low 4
weekly low 5
weekly med 4
weekly med 4
weekly med 4
weekly med 4
weekly med 4
weekly high 5
weekly high 6
weekly high 6
weekly high 7
weekly high 8
;
run ;

Krok 2: Wykonaj dwukierunkową ANOVA

Następnie użyjemy proc ANOVA do wykonania dwukierunkowej ANOVA:

 /*perform two-way ANOVA*/
proc ANOVA data =my_data;
class water sunlight;
model height = water sunlight water*sunlight;
means water sunlight / tukey cldiff ;
run ;

Krok 3: Interpretacja wyników

Pierwszą tabelą, którą chcemy przeanalizować w wynikach, jest tabela ANOVA:

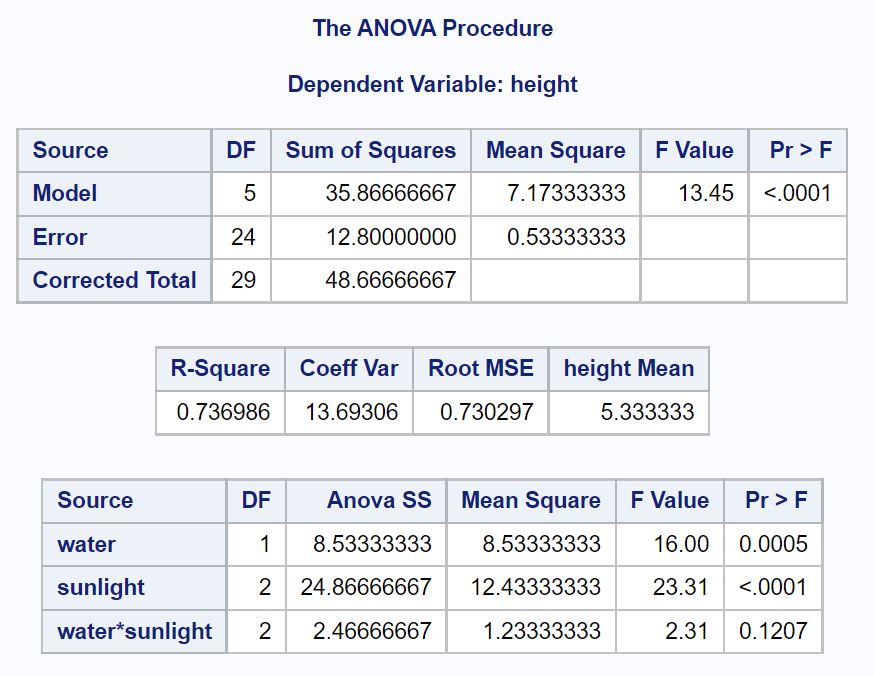
Z tej tabeli możemy zobaczyć:

• Wartość p dla wody: 0,0005
• Wartość p dla światła słonecznego: <.0001
• Wartość p dla interakcji wody i światła słonecznego: . 1207

To mówi nam, że woda i światło słoneczne są statystycznie istotnymi predyktorami wysokości rośliny i że nie ma statystycznie istotnego efektu interakcji między wodą i światłem słonecznym.

Następnie możemy sprawdzić wyniki testów post-hoc Tukeya, aby określić, które poziomy wody i światła słonecznego różnią się statystycznie istotnie.

Najpierw przyjrzymy się porównaniom post hoc Tukeya dla wody:

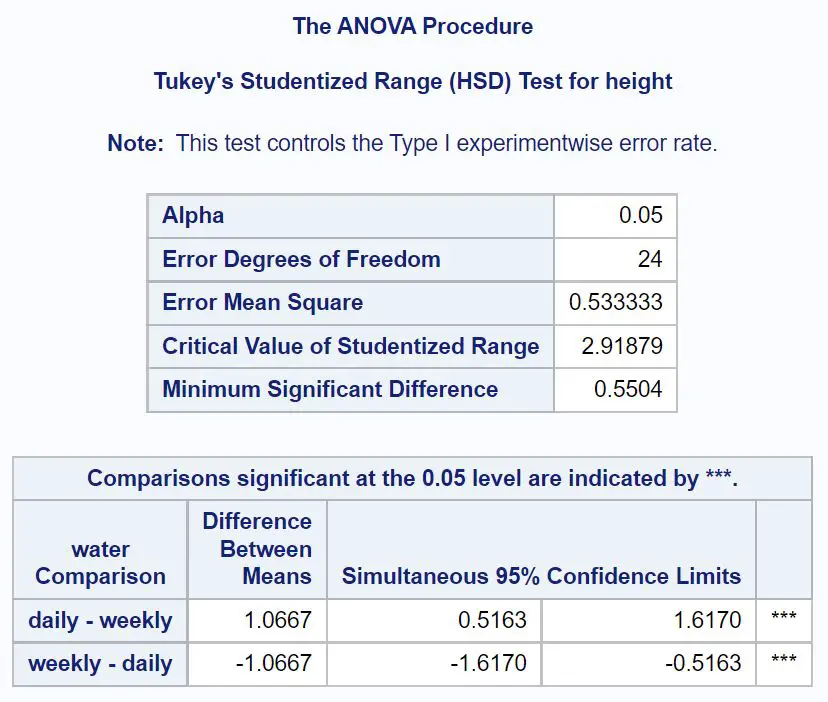
Z wyników wynika, że średnia różnica wysokości pomiędzy roślinami podlewanymi codziennie i co tydzień wyniosła 1,0667 cala.

95% przedział ufności dla różnicy w średniej wielkości wynosi [0,5163, 1,6170] . Oznacza to, że mamy 95% pewności, że prawdziwa różnica w średnim wzroście między roślinami podlewanymi codziennie a roślinami podlewanymi co tydzień wynosi od 0,5163 cala do 1,6170 cala.

Najpierw przyjrzymy się porównaniom post hoc Tukeya dla światła słonecznego:

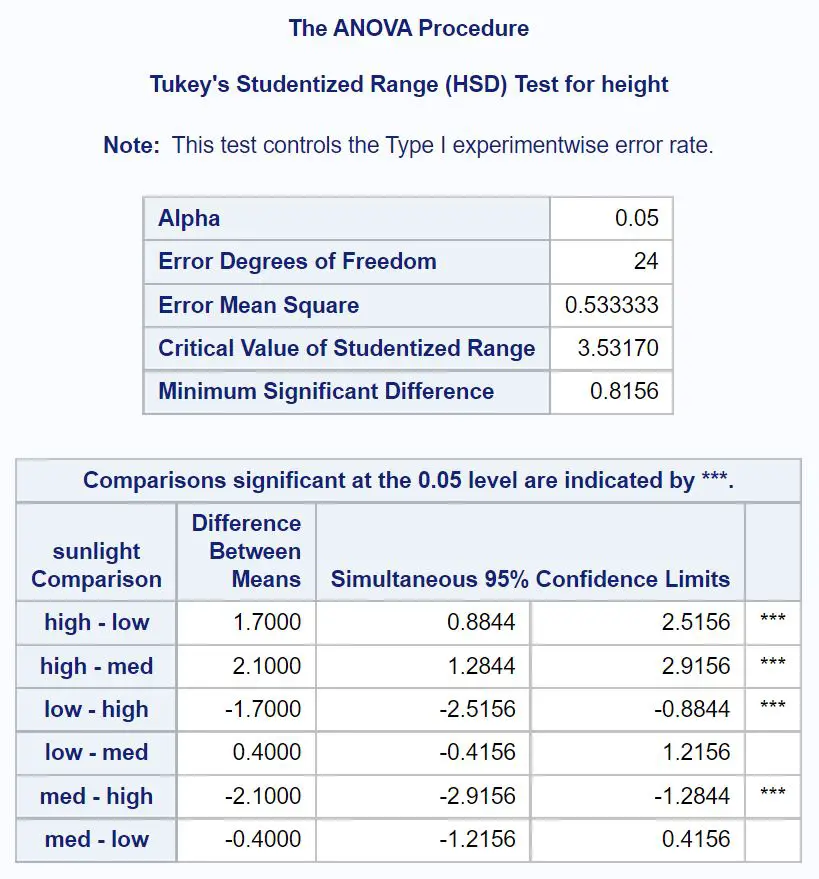
Aby dowiedzieć się, które średnie grupowe są różne, musimy sprawdzić, które porównania parami mają obok siebie gwiazdki ( *** ).

Z tabeli widać, że średnie następujących grup różnią się statystycznie istotnie:

• Wysokie lub niskie nasłonecznienie (95% CI = [0,8844, 2,5156])
• Silne lub średnie nasłonecznienie (95% CI = [1,2844, 2,9156])

Krok 4: Zgłoś wyniki

Na koniec możemy zgłosić wyniki dwuczynnikowej analizy ANOVA:

Przeprowadzono dwukierunkową analizę ANOVA w celu analizy wpływu częstotliwości podlewania i ekspozycji na słońce na wzrost roślin.

Dwuczynnikowa analiza ANOVA wykazała, że nie było statystycznie istotnej interakcji pomiędzy wpływem częstotliwości podlewania a ekspozycją na słońce (p = 0,1207).

Prosta analiza wpływu dłoni wykazała, że częstotliwość podlewania miała statystycznie istotny wpływ na wzrost roślin (p = 0,0005).

Prosta analiza wpływu dłoni wykazała, że ekspozycja na słońce miała również statystycznie istotny wpływ na wzrost roślin (p < 0,0001).

Dodatkowe zasoby

Poniższe samouczki zawierają dodatkowe informacje na temat dwukierunkowej analizy ANOVA:

Wprowadzenie do dwukierunkowej ANOVA
Jednokierunkowa czy dwukierunkowa ANOVA: kiedy je stosować?
Jak ręcznie wykonać dwukierunkową ANOVA