Dyskretny rozkład równomierny

W artykule wyjaśniono, czym jest dyskretny rozkład równomierny i jaki jest jego charakterystyczny wzór. Podobnie będziesz mógł zobaczyć graficzną reprezentację dyskretnego rozkładu równomiernego i jego właściwości.

Co to jest dyskretny rozkład równomierny?

Dyskretny rozkład równomierny to dyskretny rozkład prawdopodobieństwa, w którym wszystkie wartości są jednakowo prawdopodobne, to znaczy w dyskretnym rozkładzie równomiernym wszystkie wartości mają to samo prawdopodobieństwo wystąpienia.

Na przykład rzut kostką można zdefiniować za pomocą dyskretnego równomiernego rozkładu, ponieważ wszystkie możliwe wyniki (1, 2, 3, 4, 5 lub 6) mają to samo prawdopodobieństwo wystąpienia.

Ogólnie rzecz biorąc, dyskretny rozkład równomierny ma dwa charakterystyczne parametry aib , które określają zakres możliwych wartości , jakie może przyjąć rozkład. Zatem, gdy zmienna jest zdefiniowana przez dyskretny rozkład równomierny, jest zapisywana jako Uniform(a,b) .

Dyskretny rozkład równomierny można wykorzystać do opisania eksperymentów losowych, ponieważ jeśli wszystkie wyniki mają to samo prawdopodobieństwo, oznacza to, że eksperyment jest losowy.

Dyskretny wzór na rozkład równomierny

Teraz, gdy znamy definicję dyskretnego rozkładu równomiernego, zobaczymy, jaki jest wzór, który pozwala nam obliczyć prawdopodobieństwo pojawienia się wartości rozkładu tego typu.

Funkcja prawdopodobieństwa dyskretnego rozkładu równomiernego jest stała, a jej wartość jest równa jedności przez całkowitą liczbę możliwych wyników. Zatem wzór na dyskretny rozkład równomierny jest następujący:

Natomiast wzór na skumulowaną funkcję prawdopodobieństwa dyskretnego rozkładu równomiernego jest następujący:

Złoto

I

są charakterystycznymi parametrami dyskretnego rozkładu równomiernego.

Dyskretny rozkład równomierny

Ponieważ dyskretny rozkład równomierny może przyjmować tylko określone wartości w przedziale, jego graficzna reprezentacja składa się z punktów. Co więcej, wszystkie prawdopodobieństwa są równe, więc wszystkie punkty dyskretnego rozkładu równomiernego mają tę samą współrzędną pionową.

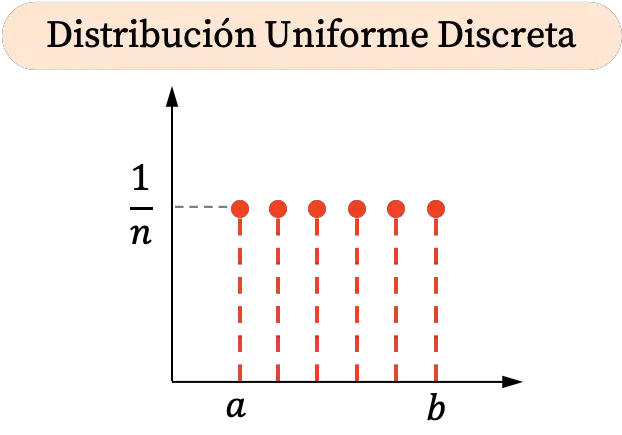
Z drugiej strony skumulowany wykres prawdopodobieństwa dyskretnego rozkładu równomiernego wygląda następująco:

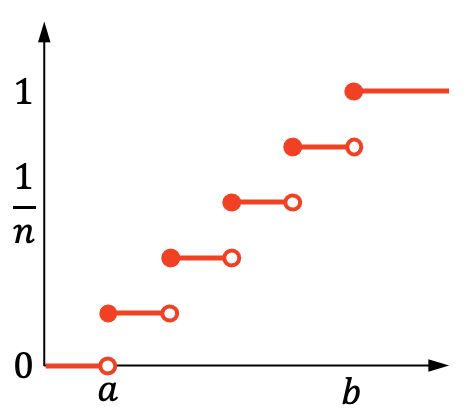
Charakterystyka dyskretnego rozkładu równomiernego

Dyskretny rozkład równomierny ma następujące cechy:

• Dyskretny rozkład równomierny definiowany jest przez dwa parametry całkowite aib , które określają zakres możliwych wartości rozkładu.

• Średnia dyskretnego rozkładu równomiernego jest równa sumie jego dwóch charakterystycznych parametrów podzielonej przez dwa.

• Mediana dyskretnego rozkładu równomiernego jest równa jej średniej, dlatego oblicza się ją za pomocą tego samego wyrażenia:

• Wariancja dyskretnego rozkładu równomiernego jest równa kwadratowi całkowitej liczby wyników minus jeden podzielonej przez dwanaście.

• Dyskretny rozkład równomierny jest symetryczny względem swojej średniej, dlatego współczynnik skośności tego rozkładu prawdopodobieństwa wynosi zero.

• Kurtozę dyskretnego rozkładu jednorodnego można obliczyć za pomocą następującego wyrażenia:

Dyskretny rozkład równomierny i ciągły rozkład równomierny

Na koniec zobaczymy, jaka jest różnica między dyskretnym rozkładem równomiernym a ciągłym rozkładem równomiernym, ponieważ są to dwa podobne typy rozkładów prawdopodobieństwa, ale różniące się znaczną różnicą.

Różnica między dyskretnym rozkładem równomiernym a ciągłym rozkładem równomiernym polega na ich możliwych wartościach. Dyskretny rozkład równomierny może przyjmować tylko określone wartości w przedziale, natomiast ciągły rozkład równomierny może przyjmować dowolną wartość w przedziale, w którym jest zdefiniowany.

Ogólnie rzecz biorąc, dyskretne rozkłady równomierne mogą przyjmować tylko wartości całkowite, podczas gdy ciągłe rozkłady równomierne mogą również przyjmować wartości dziesiętne.