Dystrybucja wersji beta

Przez Benjamin Anderson 4 sierpnia, 2023 Prawdopodobieństwo 0 komentarzy

W tym artykule wyjaśniono, czym jest dystrybucja beta i do czego służy. Podobnie będziesz mógł zobaczyć wykres rozkładu beta i właściwości tego typu rozkładu prawdopodobieństwa.

Jaka jest dystrybucja wersji beta?

Rozkład beta jest rozkładem prawdopodobieństwa zdefiniowanym na przedziale (0,1) i sparametryzowanym dwoma dodatnimi parametrami: α i β. Innymi słowy, wartości rozkładu beta zależą od parametrów α i β.

Dlatego główną cechą rozkładu beta jest to, że jego kształt można kontrolować za pomocą parametrów α i β. Dodatkowo rozkład beta służy do definiowania zmiennych losowych, których wartość mieści się w przedziale od 0 do 1.

Istnieje kilka oznaczeń wskazujących, że ciągła zmienna losowa podlega rozkładowi beta. Najczęstsze to:

$\begin{array}{c}X\sim B(\alpha,\beta)\\[2ex]X\sim Beta(\alpha,\beta)\\[2ex]X\sim \beta_{\alpha,\beta}\end{array}$

W statystykach dystrybucja beta ma bardzo różnorodne zastosowania. Na przykład rozkład beta służy do badania różnic procentowych w różnych próbkach. Podobnie w zarządzaniu projektami dystrybucja beta służy do przeprowadzania analizy Pert.

Wykres dystrybucji wersji beta

Biorąc pod uwagę definicję rozkładu beta, poniżej wykreślono funkcję gęstości i rozkład prawdopodobieństwa rozkładu beta.

Poniżej możesz zobaczyć jak wykres funkcji gęstości rozkładu beta zmienia się w zależności od parametrów α i β.

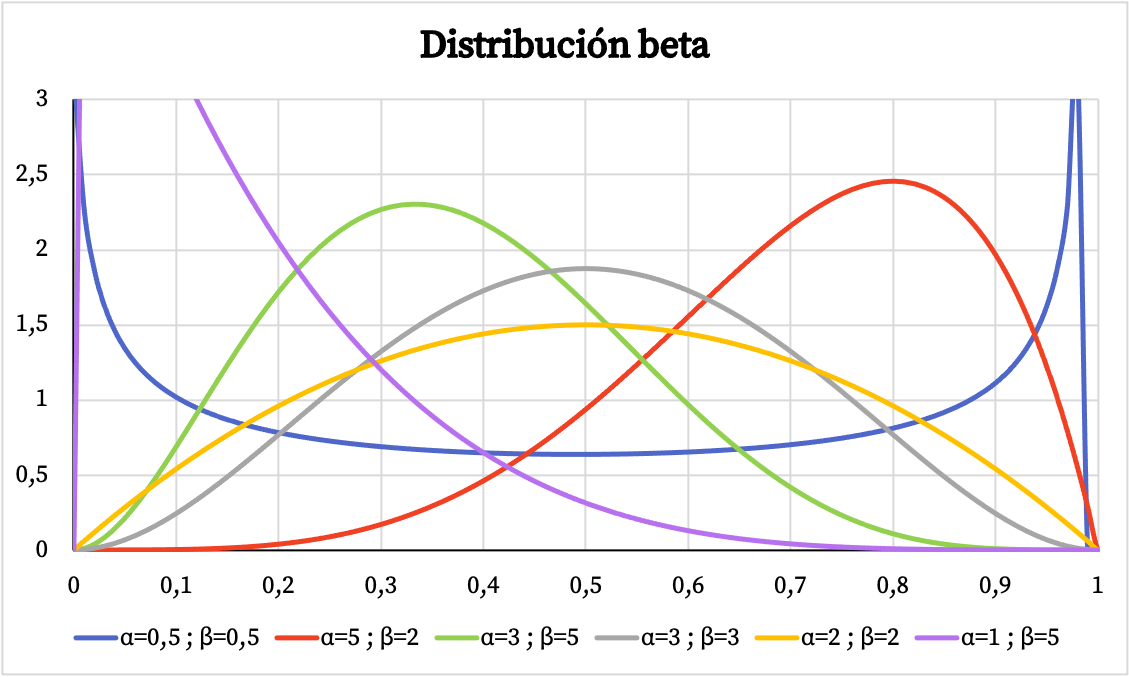
Podobnie poniżej można zobaczyć graficzną reprezentację skumulowanego prawdopodobieństwa rozkładu beta w oparciu o parametry α i β.

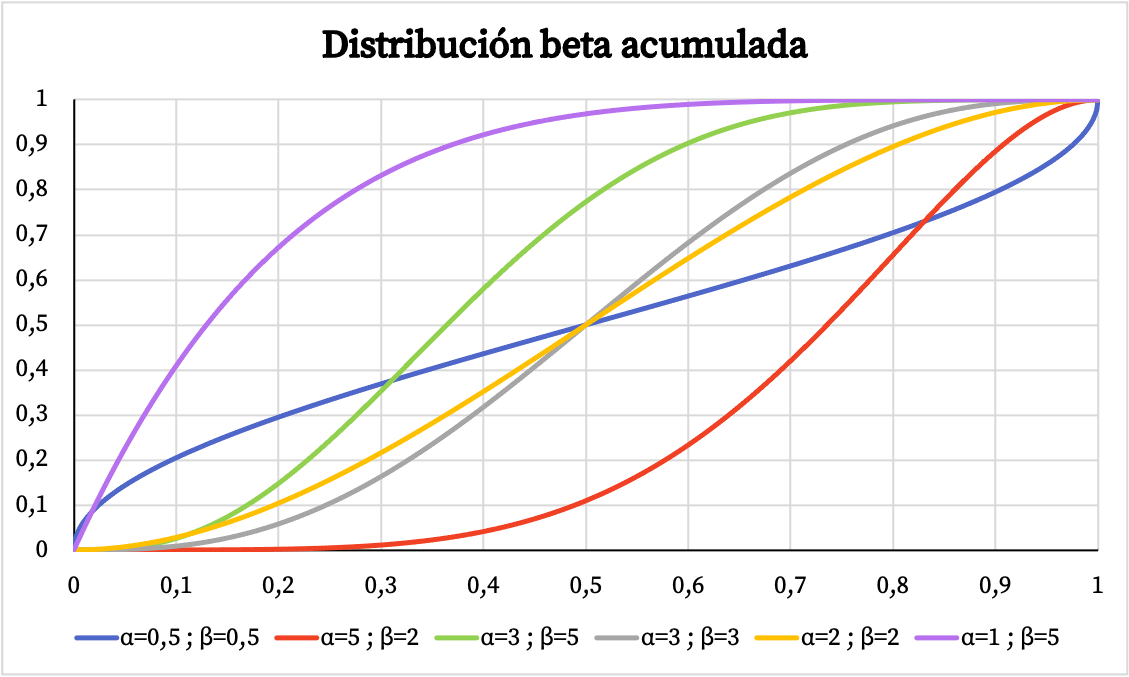
wykres skumulowanej dystrybucji wersji beta

Charakterystyka rozkładu beta

W tej sekcji zobaczymy, jakie są najważniejsze cechy dystrybucji beta.

Parametry α i β rozkładu beta są liczbami rzeczywistymi i dodatnimi.

$\begin{array}{c}\alpha >0\\[2ex] \beta >0\end{array}” title=”Rendered by QuickLaTeX.com” height=”54″ width=”44″ style=”vertical-align: 0px;”></p> </p> <ul> <li> Dziedzina rozkładu beta mieści się w zakresie od 0 do 1, przy czym oba ekstrema nie są uwzględnione.</li> </ul> <p class=$ $x\in (0,1)$

Średnia rozkładu beta jest równa wartości alfa podzielonej przez sumę alfa plus beta.

$\begin{array}{c}X\sim B(\alpha,\beta)\\[2ex] E[X]=\cfrac{\alpha}{\alpha+\beta}\end{array}$

Wariancję rozkładu beta można obliczyć za pomocą następującego wzoru:

$\begin{array}{c}X\sim B(\alpha,\beta)\\[2ex] Var(X)=\cfrac{\alpha\cdot \beta}{(\alpha+\beta+1)\cdot (\alpha+\beta)^2}\end{array}$

Dla wartości alfa i beta większych niż 1 tryb rozkładu beta można łatwo znaleźć za pomocą następującego wyrażenia:

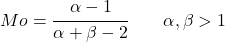
$Mo=\cfrac{\alpha-1}{\alpha+\beta-2}\qquad \alpha,\beta>1″ title=”Rendered by QuickLaTeX.com” height=”42″ width=”225″ style=”vertical-align: -16px;”></p> </p> <ul> <li> Funkcja gęstości rozkładu beta jest następująca:</li> </ul> <p class=$ $\displaystyle P[X=x]=\frac{x^{\alpha-1}(1-x)^{\beta-1}}{B(\alpha,\beta)}$

Gdzie B(α,β) jest funkcją beta, którą definiujemy jako:

$\displaystyle B(\alpha,\beta)=\int_0^1x^{\alpha-1}(1-x)^{\beta-1}dx$

Skumulowana funkcja prawdopodobieństwa rozkładu beta to:

$\displaystyle P[X\leq x]=\frac{B(x;\alpha,\beta)}{B(\alpha,\beta)}$

Gdzie B(x;α,β) jest niepełną funkcją beta, zdefiniowaną jako:

$\displaystyle B(x;\,a,b) = \int_0^x t^{a-1}\,(1-t)^{b-1}\,dt$

Jeśli X jest zmienną zdefiniowaną przez rozkład beta, to 1-X jest zmienną zdefiniowaną przez rozkład beta, którego parametry alfa i beta są odpowiednio parametrami beta i alfa pierwotnego rozkładu beta.

$X\sim B(\alpha,\beta) \ \color{orange}\bm{\longrightarrow}\color{black} \ 1-X\sim B(\beta,\alpha)$

Jeśli oba parametry alfa i beta rozkładu beta są równe 1, wówczas rozkład jest równoważny jednolitemu rozkładowi parametrów 0 i 1.

$X\sim B(1,1) \ \color{orange}\bm{\longrightarrow}\color{black} \ X\sim U(0,1)$

o autorze

Dr Benjamin Anderson

Cześć, jestem Benjamin i jestem emerytowanym profesorem statystyki, który został oddanym nauczycielem Statorials. Dzięki bogatemu doświadczeniu i wiedzy specjalistycznej w dziedzinie statystyki chętnie dzielę się swoją wiedzą, aby wzmocnić pozycję uczniów za pośrednictwem Statorials. Wiedzieć więcej

Jaka jest dystrybucja wersji beta?

Wykres dystrybucji wersji beta

Charakterystyka rozkładu beta

o autorze

Dr Benjamin Anderson

Dodaj komentarz