Dystrybucja snedecor f
W tym artykule wyjaśniono, czym jest dystrybucja Snedecor F i do czego służy. Dodatkowo będziesz mógł zobaczyć wykres rozkładu Snedecor F i jakie są jego właściwości statystyczne.
Jaka jest dystrybucja Snedecor F?
Rozkład F Snedecora , zwany także rozkładem F Fishera – Snedecora lub po prostu rozkładem F , jest ciągłym rozkładem prawdopodobieństwa stosowanym we wnioskowaniu statystycznym, szczególnie w analizie wariancji.
Jedną z właściwości rozkładu Snedecora F jest to, że jest on zdefiniowany przez wartość dwóch rzeczywistych parametrów m i n , które wskazują ich stopnie swobody. Zatem symbolem rozkładu Snedecora F jest F m, n , gdzie m i n są parametrami definiującymi rozkład.

![Rendered by QuickLaTeX.com \left.\begin{array}{c} X\sim \chi_m^2\\[2ex] Y\sim \chi_n^2\end{array}\right\}\color{orange}\bm{\longrightarrow}\color{black}\ F_{m,n}= \cfrac{X/m}{Y/n}](https://statorials.org/wp-content/ql-cache/quicklatex.com-d407869e61ca4357ffbcb40df3bd83ab_l3.png)
Rozkład Fishera-Snedecora F swoją nazwę zawdzięcza angielskiemu statystykowi Ronaldowi Fisherowi i amerykańskiemu statystykowi George’owi Snedecorowi.
W statystyce rozkład Fishera-Snedecora F ma różne zastosowania. Na przykład rozkład F Fishera-Snedecora stosuje się do porównywania różnych modeli regresji liniowej, a ten rozkład prawdopodobieństwa wykorzystuje się w analizie wariancji (ANOVA).
Schemat dystrybucji Snedecor F
Po zapoznaniu się z definicją rozkładu Snedecora F, poniżej przedstawiono wykres jego funkcji gęstości i wykres jego skumulowanego prawdopodobieństwa.
Na poniższym wykresie można zobaczyć kilka przykładów rozkładów Snedecora F o różnych stopniach swobody.
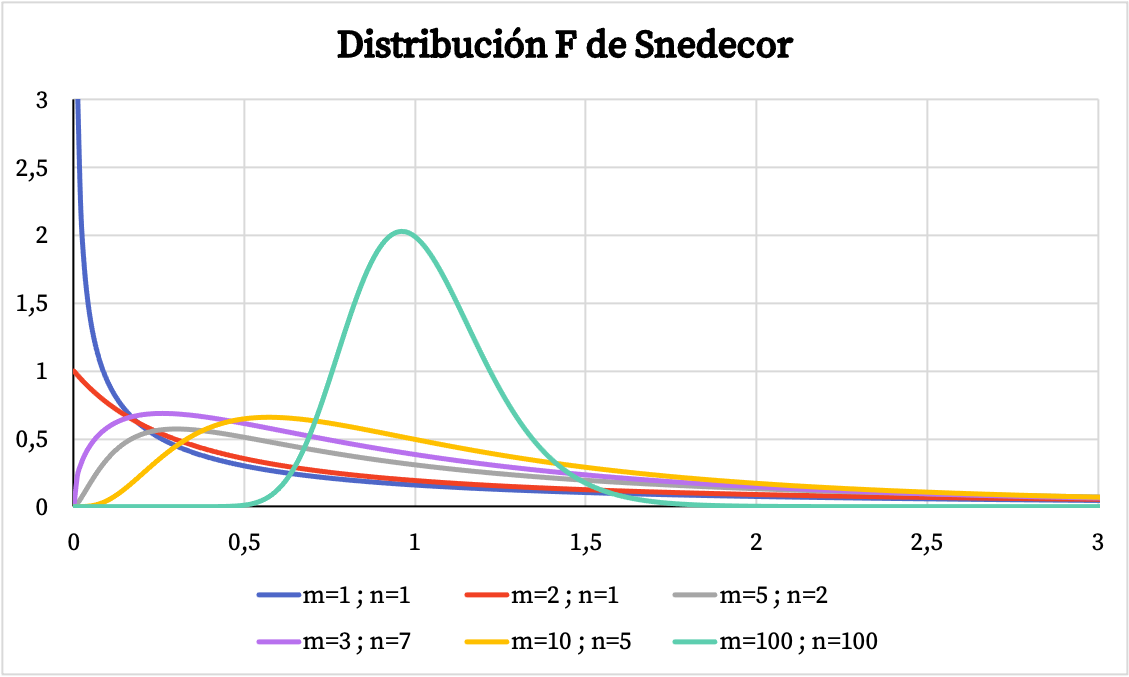
Natomiast na poniższym wykresie widać jak zmienia się wykres skumulowanej funkcji prawdopodobieństwa rozkładu Snedecora F w zależności od jego wartości charakterystycznych.
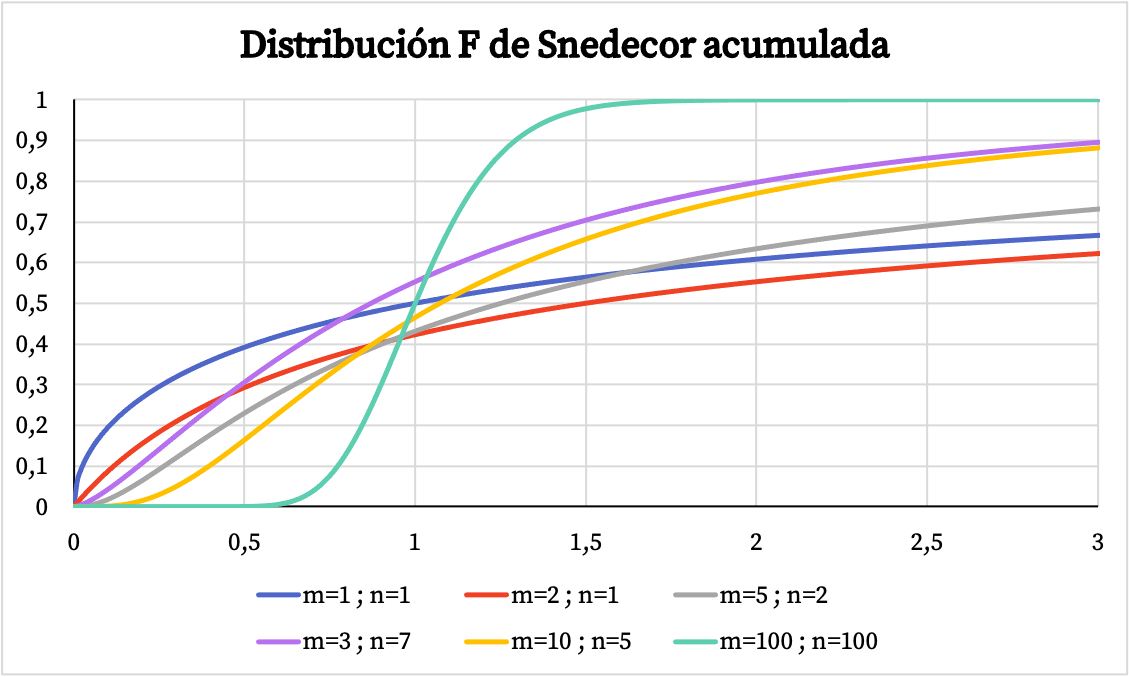
Charakterystyka rozkładu Snedecor F
Na koniec w tej sekcji przedstawiono najważniejsze cechy dystrybucji Snedecor F.
- Stopnie swobody rozkładu Snedecora F, m i n , to dwa parametry definiujące kształt rozkładu. Te charakterystyczne wartości rozkładu Snedecor F są dodatnimi liczbami całkowitymi.
![\begin{array}{c}m,n \in \mathbb{Z}\\[2ex] m,n>0\end{array}” title=”Rendered by QuickLaTeX.com” height=”54″ width=”68″ style=”vertical-align: 0px;”></p>
</p>
<ul>
<li> Dziedzina rozkładu Snedecora F składa się ze wszystkich liczb rzeczywistych większych lub równych zero.</li>
</ul>
<p class=](https://statorials.org/wp-content/ql-cache/quicklatex.com-043df156b055e7088fa83fe733825632_l3.png)
![]()
- Dla wartości n większych niż 2 średnia rozkładu Snedecor F jest równa n po odjęciu n minus 2.
![\begin{array}{c}X\sim F_{m,n}\\[2ex] E[X]=\cfrac{n}{n-2} \qquad \text{para }n>2\end{array} ” title=”Rendered by QuickLaTeX.com” height=”75″ width=”225″ style=”vertical-align: 0px;”></p>
</p>
<ul>
<li> Jeżeli parametr <em>n</em> jest większy od 2, wariancję rozkładu Snedecora F można obliczyć, stosując następujący wzór:</li>
</ul>
<p class=](https://statorials.org/wp-content/ql-cache/quicklatex.com-5861b8fbc6e7aef8cac0eb21cad00c9f_l3.png)
![\begin{array}{c}X\sim F_{m,n}\\[2ex] Var(X)=\cfrac{2n^2\cdot (m+n-2)}{m\cdot (n-2)^2\cdot (n-4)} \qquad \text{para }n>4\end{array} ” title=”Rendered by QuickLaTeX.com” height=”80″ width=”366″ style=”vertical-align: 0px;”></p>
</p>
<ul>
<li> Jeśli parametr <em>m</em> jest większy niż 2, postać rozkładu Snedecora F można obliczyć za pomocą następującego wyrażenia:</li>
</ul>
<p class=](https://statorials.org/wp-content/ql-cache/quicklatex.com-9a284413da889eec7ac2e9a95e255169_l3.png)
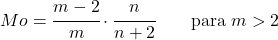
![Rendered by QuickLaTeX.com \displaystyle P[X=x]=\frac{\Gamma\left(\frac{m+n}{2}\right)}{\Gamma\left(\frac{m}{2}\right)\Gamma\left(\frac{n}{2}\right)}\left(\frac{m}{n}\right)^{\frac{m}{2}}\cdot\frac{x^{\frac{m-2}{2}}}{\left(1+\frac{mx}{n}\right)^{\frac{m+n}{2}}}](https://statorials.org/wp-content/ql-cache/quicklatex.com-06871a7baaf462b75f545a02eac7dd11_l3.png)
- Jeśli zmienna podlega rozkładowi Snedecora F o stopniach swobody m i n , to odwrotność tej zmiennej podlega rozkładowi Snedecora F o tych samych stopniach swobody, ale zmienia się kolejność jej wartości.
![]()
- Rozkład Studenta ma następujący związek z rozkładem Snedecor F:
![]()